40 câu hỏi trắc nghiệm thuộc 299 câu trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết(P1)

Câu 1:

Một chiếc vòng đeo tay gồm 20 hạt giống nhau. Hỏi có bao nhiêu cách cắt chiếc vòng đó thành 2 phần mà số hạt ở mỗi phần đều là số lẻ?

A. 90.

B. 5.

C. 180.

D. 10 .

Xem đáp án

Chọn B

Ta có: 20 = 1 + 19 = 3 + 17 = 5 + 15 = 7 + 13 mà vòng đeo tay gồm 20 hạt giống nhau nên có 5 cách cắt chiếc vòng đó thành 2 phần mà số hạt ở mỗi phần đều là số lẻ.

Câu 2:

Cho đa giác đều 2019 đỉnh. Khi đó số tứ giác mà mỗi đỉnh được lấy từ các đỉnh của đa giác đều đã cho và không có cạnh nào là cạnh của đa giác đều đã cho là:

A. $2019 C_{2016}^{4}$

B. $2019 C_{2019}^{4}$ - 2019

C. 504,75 $2019 C_{2016}^{4}$

D. $2019 C_{2019}^{4}$

Xem đáp án

Chọn C

Câu 3:

Một công việc để hoàng thành bắt buộc phải trải qua hai bước, bước thứ nhất có m cách thực hiện và bước thứ hai có n cách thực hiện. Số cách để hoàn thành công việc đã cho bằng

A. m + n

B. $m^{n}$

C. mn

D. $n^{m}$

Xem đáp án

Chọn C

Theo quy tắc nhân ta có số cách là mn

Câu 4:

Từ các chữ số 1,2,3,....,9 lập được bao nhiêu số có 3 chữ số đôi một khác nhau.

$A . 3^{9}$

$B . A_{9}^{3}$

$C . 9^{3}$

$D . C_{9}^{3}$

Xem đáp án

Chọn B

Lấy ra 3 chữ số từ 9 chữ số và sắp xếp 3 chữ số đó theo thứ tự, mỗi cách sắp xếp tạo nên 1 số có 3 chữ số khác nhau. Như vậy, có $A_{9}^{3}$ số cần tìm.

* Nhận xét: Mục đích bài toán là phân biệt hai khái niệm: Chỉnh hợp và tổ hợp. Học sinh có thể giải bài này bằng phương pháp nhân: 9.8.7, và so sánh với 4 đáp án. Hai chỉnh hợp khác nhau thì có thể khác nhau về phần tử hoặc khác nhau về thứ tự các phần tử. Hai tổ hợp khác nhau thì khác nhau về phần tử.

*Lý thuyết Chỉnh hợp

- Cho tập hợp A có n phần tử và cho số nguyên k, (1 $\leq$ k $\leq$ n). Khi lấy k phần tử của A và sắp xếp chúng theo một thứ tự, ta được một chỉnh hợp chập k của n phần tử của A (gọi tắt là một chỉnh hợp n chập k của A).

- Số các chỉnh hợp chập k của một tập hợp có n phần tử là: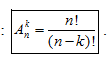

- Một số qui ước:

*Lý thuyết Tổ hợp

- Cho tập hợp A có n phần tử và cho số nguyên k, (1 $\leq$ k $\leq$ n). Mỗi tập hợp con của A có phần tử được gọi là một tổ hợp chập k của n phần tử của A.

- Số các chỉnh hợp chập k của một tập hợp có n phần tử là :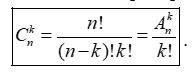

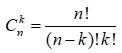- Một số quy ước: với qui ước này ta có đúng với số nguyên dương k, thỏa 0 $\leq$ k $\leq$ n

PT 14.1. Chọn B

TH1

TH2: vì

Như vậy, có số cần tìm

PT 14.2.

Chọn C

Mỗi tập con có 3 phần tử thuộc tập {1,2,...,9} xác định duy nhất một số có 3 chữ số tăng dần từ trái qua phải (đảm bảo chữ số đầu tiên khác 0).

Mỗi tập con có 3 phần tử thuộc tập {0,1,2....,9} xác định duy nhất một số có 3 chữ số giảm dần từ trái qua phải.

Như vậy, có số cần tìm.

Câu 5:

Một lớp học có 12 bạn nam và 10 bạn nữ. Số cách chọn hai bạn trực nhật sao cho có cả nam và nữ là

A. 120

B. 231

C. 210

D. 22

Xem đáp án

Chọn A

Số cách chọn một bạn nam là 12 cách.

Số cách chọn một bạn nữ là 10 cách

Vậy số cách chọn hai bạn trực nhật có cả nam và nữ là 12.10 = 120 (cách)

Câu 6:

Một tổ có 10 học sinh. Số cách chọn ra hai bạn học sinh làm tổ trưởng và tổ phó là:

A. 10

B. 90.

C. 45.

D. 24.

Xem đáp án

Chọn B

Số cách chọn ra hai bạn học sinh làm tổ trưởng và tổ phó từ 10 học sinh là $A_{2}^{10} = 90$

Câu 7:

Có bao nhiêu cách chọn ra một tổ trưởng và một tổ phó từ một tổ có 10 người? Biết khả năng được chọn của mỗi người trong tổ là như nhau.

A. 100

B. 90

C. 50

D. 45

Xem đáp án

Chọn B

Chọn một tổ trưởng từ 10 người có 10 cách chọn.

Chọn một tổ phó từ 9 người còn lại có 9 cách chọn.

Theo quy tắc nhân, ta có 10.9 = 90 cách chọn thỏa yêu cầu bài toán.

Câu 8:

Nhãn mỗi chiếc ghế trong một hội trường gồm hai phần : phần đầu là một chữ cái ( trong bảng 24 chữ cái tiếng Việt ), phần thứ hai là một số nguyên dương nhỏ hơn 26. Hỏi có nhiều nhất bao nhiêu chiếc ghế được ghi nhãn khác nhau ?

A. 624

B. 600

C. 49

D. 648

Xem đáp án

Chọn B

Gọi n là số nguyên dương nhỏ hơn 26.

Ta có : 0 < n < 26,

Chọn một chữ cái trong 24 chữ cái có 24 cách.

Chọn một số nguyên dương ( nhỏ hơn 26) có 25 cách.

Theo quy tắc nhân có : 24.25 = 600 cách ghi nhãn khác nhau.

Câu 9:

Trong một lớp học có 20 học sinh nam và 24 học sinh nữ. Giáo viên chủ nhiệm cần chọn hai học sinh: 1 nam và 1 nữ tham gia đội cờ đỏ. Hỏi giáo viên chủ nhiệm đó có bao nhiêu cách chọn?

A. 44

B. 480

C. 20

D. 24

Xem đáp án

Chọn B

Câu 10:

Một bộ đồ chơi ghép hình gồm các miếng nhựa. mỗi miếng nhựa được đặc trưng bởi ba yếu tố: màu sắc, hình dạng và kích cỡ. Biết rằng có 4 màu (xanh, đỏ, vàng, tím), có 3 hình dạng (hình tròn, hình vuông, hình tam giác) và 2 kích cỡ (to, nhỏ). Hộp đồ chơi đó có số miếng nhựa nhiều nhất là:

A. 24

B. 9

C. 26

D. 20

Xem đáp án

Chọn A

Câu 11:

Gọi A là tập hợp tất cả các số có dạng $\bar{a b c}$ với a, b, c $\in \{1, 2, 3, 4\}$ . Số phần tử của tập hợp A là

$A . C_{3}^{4}$

$B . 3^{4}$

$C . A_{4}^{3}$

$D . 4^{3}$

Xem đáp án

Chọn D

Để lập một số có dạng $\bar{a b c}$ với a, b, c $\in \{1, 2, 3, 4\}$ . ta thực hiện:

Chọn 1 số vào vị trí a có 4 cách.

Chọn 1 số vào vị trí b có 4 cách.

Chọn 1 số vào vị trí c có 4 cách.

Vậy có 4.4.4 = $4^{3}$ số trong tập

Câu 12:

Từ các số 0, 1, 3, 4, 5, 7 có thể lập được bao nhiêu số tự nhiên có sáu chữ số khác nhau?

A. 720

B. 600

C. 625

D. 240

Xem đáp án

Chọn B

Gọi số tự nhiên có sáu chữ số cần tìm là $\bar{a b c d e f}, a ⩾ \neq$ 0 ,

Chọn 1 có 5 cách chọn.

Sau khi chọn a còn 5 chữ số xếp vào các vị trí b, c, d, e, f nên có 5! cách chọn.

Theo quy tắc nhân có 5.5! = 600 (số).

Câu 13:

Tập hợp A = {1,2,....,10} Số cách chọn ra 2 phần tử của A gồm 1 phần tử chẵn và 1 phần tử lẻ bằng

$A . C_{2}^{10}$

$B . {(C_{10}^{1})}^{2}$

$C . {(C_{1}^{5})}^{2}$

$D . C_{1}^{10} . C_{1}^{9}$

Xem đáp án

Chọn C

Ta có tập A gồm 5 số chẵn và 5 số lẻ. Do đó số cách chọn ra 2 phần tử gồm 1 phần tử chẵn và 1 phần tử lẻ là ${(C 15)}^{2}$

Câu 14:

Từ các số 1, 2, 3, 4, 5, 6, 7 lập được bao nhiêu số tự nhiên có sáu chữ số đôi một khác nhau trong đó các chữ số 1, 2, 3 luôn có mặt và đứng cạnh nhau?

A. 96

B. 480

C. 576

D. 144

Xem đáp án

Chọn C

Số cách chọn 3 số bất kì từ tập {4;5;6;7} là $C_{3}^{4}$

Do 1, 2, 3 luôn đứng cạnh nhau nên ta xem chúng như một phần tử.

Số các số tự nhiên có sáu chữ số đôi một khác nhau trong đó 1, 2, 3 luôn đứng cạnh nhau là 4!. $C_{3}^{4}$ .3! = 576 số.

Câu 15:

Cho hai đường thẳng $d_{1}$ và $d_{2}$ song song với nhau. Trên đường thẳng $d_{1}$ cho 5 điểm phân biệt, trên đường thẳng $d_{2}$ cho 7 điểm phân biệt. Số tam giác có đỉnh là các điểm trong 12 điểm đã cho là:

A. 350.

B. 210.

C. 175.

D. 220.

Xem đáp án

Chọn C

* Số tam giác có 2 đỉnh thuộc $d_{1}$ và 1 đỉnh thuộc $d_{2}$ là: .

* Số tam giác có 1 đỉnh thuộc $d_{1}$ và 2 đỉnh thuộc $d_{2}$ là: .

Vậy có 70 + 105 = 175 tam giác.

Câu 16:

Có bao nhiêu số tự nhiên có 4 chữ số được viết từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8, 9 sao cho số đó chia hết cho 15?

A. 234.

B. 132.

C. 243.

D. 432.

Xem đáp án

Chọn C

Gọi số cần tìm là N = $\bar{a b c d}$ . Do N chia hết cho 15 nên N phải chia hết cho 3 và 5, vì vậy d có 1 cách chọn là bằng 5 và a + b + c + d chia hết cho 3.

Do vai trò các chữ số a, b, c như nhau, mỗi số a và b có 9 cách chọn nên ta xét các trường hợp:

TH1: a + b + d chia hết cho 3, khi đó c $⋮$ 3 => c $\in$ {3;6;9}, suy ra có 3 cách chọn c.

TH2: a + b + d chia 3 dư 1, khi đó c chia 3 dư 2 => c $\in$ {2;5;8}, suy ra có 3 cách chọn c.

TH3: a + b + d chia 3 dư 2, khi đó c chia 3 dư 1 => c $\in$ {1;4;7} suy ra có 3 cách chọn .

Vậy trong mọi trường hợp đều có 3 cách chọn c nên có tất cả: 9.9.3.1 = 243 số thỏa mãn.

Câu 17:

Cho tập hợp S = {1;2;3;4;5;6}. Gọi M là tập hợp các số tự nhiên có 6 chữ số đôi một khác nhau lấy từ S sao cho tổng của các chữ số hàng đơn vị , hàng chục và hàng trăm lớn hơn tổng các chữ số còn lại là 3. Tính tổng của các phần tử của tập hợp M.

A. T = 11003984

B. T = 36011952

C. T = 12003984

D. T = 18005967

Xem đáp án

Chọn B

Gọi số cần tìm thỏa mãn điều kiện bài toán là $\bar{a b c d e f}$ trong đó a,b,c,d,e,f $\in$ S và đôi một khác nhau. Theo bài ra ta có

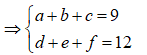
Có .

Ta có các cặp 3 số khác nhau từ S có tổng bằng 9 là .

Câu 18:

Cho một bảng ô vuông 3x3.

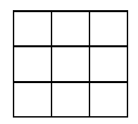
Điền ngẫu nhiên các số 1, 2, 3, 4, 5, 6, 7, 8, 9 vào bảng trên (mỗi ô chỉ điền một số). Gọi A là biến cố “mỗi hàng, mỗi cột bất kì đều có ít nhất một số lẻ”. Xác suất của biến cố A bằng

A. P(A) = $\frac{1}{3}$

B. P(A) = $\frac{10}{21}$

C. P(A) = $\frac{5}{7}$

D. P(A) = $\frac{1}{56}$

Xem đáp án

Chọn C

Số phần tử của không gian mẫu

Gọi A là biến cố “mỗi hàng, mỗi cột bất kì đều có ít nhất một số lẻ”.

$\bar{A}$ là biến cố “có một hàng, hoặc một cột đều là số chẵn”

Vì có 4 số chẵn nên chỉ có một hàng hoặc một cột xếp toàn số chẵn

Có 6 cách chọn ra một hàng hoặc hoặc một cột để xếp 3 số chẵn.

Có 6 cách chọn một ô không thuộc hàng đó để xếp tiếp 1 số chẵn nữa

Có 4! cách xếp 4 số chẵn và 5! xếp 5 số lẻ.

Vậy xác xuất .

Câu 19:

Lấy ngẫu nhiên một số tự nhiên có 9 chữ số khác nhau. Tính xác suất để số đó chia hết cho 3.

A. $\frac{17}{81}$

B. $\frac{11}{27}$

C. $\frac{1}{9}$

D. $\frac{5}{8}$

Xem đáp án

Chọn B

Ta có:

Ta thấy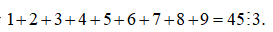

Ta chon 9 số không có số 0 thì được 9! cách.

Ta Chọn có số 0 thì trong dãy số phải bỏ ra 3 hoặc 6 hoặc 9 nên có 3.8.8! cách

Do đó

Vậy P(A) = $\frac{11}{27}$

Câu 20:

Gọi S là tập hợp các số tự nhiên gồm bốn chữ số đôi một khác nhau được lấy từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8, 9. Chọn ngẫu nhiên một số từ S. Tính xác suất P để được một số chia hết cho 11 và tổng bốn chữ số của nó cũng chia hết cho 11.

$A . P = \frac{1}{126}$

$B . P = \frac{2}{63}$

$C . P = \frac{1}{63}$

$D . P = \frac{3}{126}$

Xem đáp án

Chọn C

Ta có

Gọi số tự nhiên cần tìm có bốn chữ số là $\bar{a b c d}$

Vì $\bar{a b c d}$ chia hết cho 11 nên (a + c) - (b + d) $⋮$ 11

=> (a + c) - (b + d) = 0 hoặc (a + c) - (b + d) = 11 hoặc (a + c) - (b + d) = -11 do

Theo đề bài ta cũng có a + b + c + d chia hết cho 11

Mà

hoặc

Vì nên (a + c) - (b + d) và a + b + c + d cùng tính chẵn, lẻ

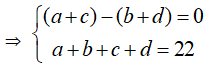
(do các trường hợp còn lại không thỏa mãn) => (a,c) và (b,d) là một trong các cặp số:

- Chọn 2 cặp trong số 4 cặp trên ta có $C_{4}^{2}$ cách.

- Ứng với mỗi cách trên có 4 cách chọn a; 1 cách chọn c; 2 cách chọn b; 1 cách chọn d.

Vậy xác suất cần tìm là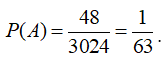

Câu 21:

Cho tập A = {3;4;5;6}. Tìm số các số tự nhiên có bốn chữ số được thành lập từ tập A sao cho trong mỗi số tự nhiên đó, hai chữ số 3 và 4 mỗi chữ số có mặt nhiều nhất 2 lần, còn hai chữ số 5 và 6 mỗi chữ số có mặt không quá 1 lần.

A. 24

B. 30

C. 102

D. 360

Xem đáp án

Chọn C

Ta có thể chia làm bốn trường hợp sau

TH1: Số 5 có mặt một lần, số 6 có mặt một lần.( Bao gồm các khả năng sau: mỗi số có mặt một lần hoặc một số 5, một số 6 hai số 3 hoặc một số 5, một số 6 hai số 4)

Số các số được tạo thành là: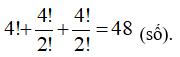

TH2: Số 5 có mặt một lần, số 6 không có mặt.

Số các số được tạo thành là: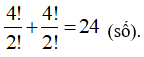

TH3: Số 6 có mặt một lần, số 5 không có mặt.

Số các số được tạo thành là: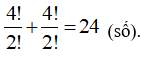

TH4: Số 5 và số 6 không có mặt.( Số 3 và số 4 mỗi số có mặt đúng hai lần)

Số các số được tạo thành là: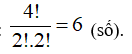

Vậy có thể lập được 102 số thỏa mãn đề bài.

Câu 22:

Với k và n là các số nguyên dương tùy ý thỏa mãn k $\leq$ n, mệnh đề nào dưới đây sai?

$A . C_{n}^{k} = C_{n}^{n - k}$

$B . C_{n}^{k} = \frac{A_{n}^{k}}{k!}$

$C . C_{n}^{k - 1} + C_{n}^{k} = C_{n + 1}^{k}$

$D . C_{n}^{k} = C_{n}^{k}$

Xem đáp án

Chọn D

Dựa vào lý thuyết hoán vị, chỉnh hợp, tổ hợp

Trắc nghiệm: Dùng máy tính chọn các giá trị cụ thể.

Câu 23:

Với k và n là hai số nguyên dương tùy ý thỏa mãn k $\leq$ n. Công thức tính số tổ hợp chập k của n phần tử là

$A . C_{n}^{k} = \frac{n!}{(n - k)! k!}$

$B . A_{n}^{k} = \frac{n!}{(n - k)!}$

$C . C_{n}^{k} = \frac{n!}{(n - k)!}$

$D . A_{n}^{k} = \frac{n!}{(n - k)! k!}$

Xem đáp án

Chọn A

Công thức tính số tổ hợp chập k của n phần tử là: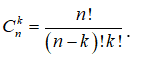

Câu 24:

Có bao nhiêu cách xếp chỗ ngồi cho 4 bạn học sinh vào dãy có 4 ghế?

A. 8 cách.

B. 12 cách.

C. 24 cách.

D. 4 cách.

Xem đáp án

Chọn C

Số cách xếp 4 bạn học sinh vào dãy có 4 ghế là: 4! = 24 cách.

Câu 25:

Cho trước 5 chiếc ghế xếp thành một hàng ngang. Số cách xếp ba bạn A, B, C vào 5 chiếc ghế đó sao cho mỗi bạn ngồi một ghế là

A. $C_{5}^{3}$

B. 6

C. $A_{5}^{3}$

D. 15

Xem đáp án

Chọn C

Cách 1: Mỗi cách xếp thỏa mãn yêu cầu bài toán chính là một chỉnh hợp chập 3 của 5 phần tử nên số cách xếp là $A_{5}^{3}$ (cách).

Cách 2: Có 5 cách xếp bạn A, với mỗi cách xếp bạn A thì có 4 cách xếp bạn B, với mỗi cách xếp bạn A và B thì có 3 cách xếp bạn C. Vậy theo qui tắc nhân có 5.4.3 = 60(cách).

Câu 26:

Có bao nhiêu cách xếp chỗ ngồi cho bốn bạn học sinh vào bốn chiếc ghế kê thành một hàng ngang?

A. 24

B. 4

C. 12

D. 8

Xem đáp án

Chọn A

Mỗi cách xếp chỗ cho bốn bạn học sinh vào bốn chiếc ghế kê thành một hàng ngang là một hoán vị của 4 phần tử. Do đó có 4! = 24 cách.

Câu 27:

Một tổ học sinh có 5 học sinh nam và 7 học sinh nữ. Có bao nhiêu cách chọn 4 học sinh của tổ để tham ra một buổi lao động?

$A . C_{5}^{4} + C_{7}^{4}$

$B . 4!$

$C . A_{12}^{4}$

$D . C_{12}^{4}$

Xem đáp án

Chọn D

Tổng số học sinh của tổ là: 5 + 7 = 12.

Số cách cách chọn 4 học sinh của tổ để tham ra một buổi lao động là tổ hợp chập 4 của 12 phần tử: $C_{4}^{12}$ .

Câu 28:

Với k, n là hai số nguyên dương tùy ý k $\leq$ n, mệnh đề nào dưới đây đúng?

$A . A_{n}^{k} = \frac{n!}{k! (n - k)!}$

$B . A_{n}^{k} = \frac{n!}{(n - k)!}$

$C . A_{n}^{k} = \frac{n!}{k!}$

$D . A_{n}^{k} = \frac{k! n!}{(n - k)!}$

Xem đáp án

Chọn B

Ta có: $A_{n}^{k} = \frac{n!}{(n - k)!}$

Câu 29:

Trong các mệnh đề sau, mệnh đề nào sai?

A. $C_{n}^{k} = \frac{n!}{k! (n - k)!} (0 \leq k \leq n)$

B. $A_{n}^{k} = \frac{n!}{(n - k)!} (1 \leq k \leq n)$

C. $C_{n}^{k} = k! A_{n}^{k} (0 \leq k \leq n)$

D. $P_{n} = n! (n \geq 1)$

Xem đáp án

Chọn C

Theo công thức ta có: 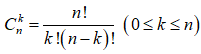nên A đúng

$A_{n}^{k} = \frac{n!}{(n - k)!} (1 \leq k \leq n)$ do đó B đúng.

$P_{n} = n! (n \geq 1)$ D đúng

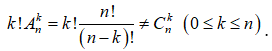Vậy đáp án C sai.

Câu 30:

Với k và n là hai số nguyên dương tùy ý thỏa mãn k $\leq$ n, mệnh đề nào dưới đây là đúng?

A. $A_{n}^{k} = \frac{n!}{k! (n - k)!}$

B. $A_{n}^{k} = \frac{n!}{k! (n - k)!}$

C. $A_{n}^{k} = \frac{n!}{k!}$

D. $A_{n}^{k} = \frac{k!}{n! (n - k)!}$

Xem đáp án

Chọn B

Số các chỉnh hợp chập k của n phần tử là: $A_{n}^{k} = \frac{n!}{k! (n - k)!}$

Câu 31:

Số cách xếp 4 học sinh vào một dãy ghế dài gồm 10 ghế, mỗi ghế chỉ một học sinh ngồi bằng

$A . C_{10}^{4}$

$B . 10^{4}$

$C . A_{10}^{4}$

$D . 4^{10}$

Xem đáp án

Chọn C

Câu 32:

Số tập con gồm đúng 3 phần tử của tập hợp gồm 10 phần tử bằng

$A . A_{10}^{3}$

$B . 3^{10} - 1$

$C . C_{10}^{3}$

$D . 3^{10}$

Xem đáp án

Chọn C

Lấy đúng 3 phần tử của tập hợp gồm 10 phần tử là một tổ hợp chập 3 của 10.

Do đó, số tập con cần tìm là $C_{10}^{3}$ .

Câu 33:

Kí hiệu: $C_{n}^{k}$ (với k; n là những số nguyên dương và k $\leq$ n) có ý nghĩa là

A. Chỉnh hợp chập k của n phần tử.

B. Số tổ hợp chập k của n phần tử.

C. Tổ hợp chập k của n phần tử.

D. Số chỉnh hợp chập k của n phần tử.

Xem đáp án

Chọn B

Câu 34:

Số tập hợp con có 3 phần tử của một tập hợp có 7 phần tử là :

$A . \frac{7!}{3!}$

$B . C_{3}^{7}$

$C . A_{3}^{7}$

$D . 21$

Xem đáp án

Chọn B

Câu 35:

Từ các chữ số 1, 2, 3, 4, 5, 6. Có thể lập được bao nhiêu số có 3 chữ số khác nhau?

A. 216

B. 120

C. 504

D. 6

Xem đáp án

Chọn B

Mỗi số có ba chữ số khác nhau lập được từ các chữ số 1, 2, 3, 4, 5, 6 là một chỉnh hợp chập 3 của 6 phần tử . Nên số

các số lập được là $A_{6}^{3}$ = 120 .

Câu 36:

Trong mặt phẳng cho tập S gồm 10 điểm trong đó không có 3 điểm nào thẳng hàng. Có bao nhiêu tam giác có 3 đỉnh đều thuộc S?

A. 720.

B. 120.

C. 59049.

D. 3628800.

Xem đáp án

Chọn B

Mỗi tam giác cần 3 đỉnh thuộc S, mỗi tam giác được tạo thành là một tổ hợp chập 3 của 10 phần tử.

Vậy số tam giác thỏa mãn là $C_{10}^{3}$ = 120.

Mức độ nhận biết, thông hiểu

Câu 37:

Số tập con có 3 phần tử của một tập hợp có 7 phần tử là

$A . \frac{7!}{3!}$

$B . C_{7}^{3}$

$C . 7$

$D . D_{7}^{3}$

Xem đáp án

Chọn B

Mỗi tập con gồm 3 phần tử là một tổ hợp chập 3 của 7 phần tử. Vậy có $C_{7}^{3}$ tập con.

Câu 38:

Cho tập hợp X có 20 phần tử. Số tập con gồm 3 phần tử của X là

$A . 20^{3}$

$B . A_{20}^{3}$

$C . C_{20}^{3}$

$D . A_{20}^{17}$

Xem đáp án

Chọn C

Số tập con chứa 3 phần tử lấy từ tập 3 bằng số tổ hợp chập 3 của 20 là $C_{20}^{3}$

Câu 39:

Kí hiệu $C_{n}^{k}$ là số tổ hợp chập k của n phần tử (0 $\leq$ k $\leq$ n). Mệnh đề nào sau đây đúng?

$A . C_{n}^{k} = \frac{n!}{(n - k)!}$

$B . C_{n}^{k} = \frac{n!}{k!}$

$C . C_{n}^{k} = \frac{n!}{k! (n - k)!}$

$D . C_{n}^{k} = \frac{n!}{k! (n - k)!}$

Xem đáp án

Chọn D

Câu 40:

Với k và n là hai số nguyên dương tùy ý thỏa mãn k $\leq$ n, mệnh đề nào dưới đây đúng?

$A . A_{n}^{k} = \frac{n!}{k!}$

$B . A_{n}^{k} = n!$

$C . A_{n}^{k} = \frac{n!}{k! (n - k)!}$

$D . A_{n}^{k} = \frac{n!}{(n - k)!}$

Xem đáp án

Chọn D

CHỌN BỘ SÁCH BẠN MUỐN XEM

299 bài trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết

299 câu trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết(P1)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm