Trắc nghiệm Toán 11: Ôn tập chương 7 có đáp án
-
1061 lượt thi
-
24 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Cho hai đường thẳng a và b chéo nhau. Có bao nhiêu mặt phẳng chứa a và song song với b?
 Xem đáp án
Xem đáp án
Cho hai đường thẳng chéo nhau,
có duy nhất một mặt phẳng qua
đường thẳng này và song song với đường thẳng kia.
Đáp án cần chọn là: D
Câu 2:
Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?
 Xem đáp án
Xem đáp án
A sai. Trong trường hợp 3 điểm phân biệt thẳng
hàng thì sẽ có vô số mặt phẳng chứa 3 điểm thẳng hàng đã cho.
B sai. Trong trường hợp điểm thuộc đường thẳng đã cho,
khi đó ra chỉ có 1 đường thẳng, có vô số mặt phẳng đi qua đường thẳng đó.
D sai. Trong trường hợp 4 điểm phân biệt thẳng hàng thì
có vô số mặt phẳng đi qua 4 điểm đó hoặc trong trường
hợp 4 điểm không đồng phẳng thì sẽ không tạo
được mặt phẳng nào đi qua cả 4 điểm.
Đáp án cần chọn là: C
Câu 3:
Tìm khẳng định đúng trong các khẳng định sau.
 Xem đáp án
Xem đáp án
A. Đúng.
B. Sai vì hai mặt phẳng có thể trùng nhau.
C. Sai vì ba giao tuyến có thể song song hoặc trùng nhau.
D. Sai hai đường thẳng đó có thể trùng nhau hoặc chéo nhau hoặc cắt nhau.
Đáp án cần chọn là: A
Câu 4:
Trong các mệnh đề sau, mệnh đề nào sai?
 Xem đáp án
Xem đáp án
Mệnh đề “Hai đường thẳng không có điểm chung
thì song song với nhau” chỉ đúng trong mặt phẳng,
còn trong không gian thì hai đường thẳng không
có điểm chung thì hoặc song song với nhau hoặc chéo nhau.
Đáp án cần chọn là: A
Câu 6:
Trong không gian cho bốn điểm không đồng phẳng. Có thể xác định được bao nhiêu mặt phẳng phân biệt từ các điểm đã cho?
 Xem đáp án
Xem đáp án
Số mặt phẳng tạo thành là số
cách chọn 3 trong 4 điểm đã cho.
Vậy có 4 mặt phẳng.
Đáp án cần chọn là: B
Câu 7:
Tìm khẳng định sai trong các khẳng định sau đây?
 Xem đáp án
Xem đáp án
Nếu mặt phẳng (P) có chứa hai đường thẳng phân biệt
và hai đường thẳng đó cùng song song với mặt phẳng
(Q) thì mặt phẳng (P) song song với mặt phẳng (Q)
là mệnh đề sai khi hai đường thẳng đó song song
với nhau (hai đường thẳng đó phải cắt nhau mới đúng).
Đáp án cần chọn là: D
Câu 11:
Cho bốn mệnh đề sau:
(I) Nếu hai mặt phẳng và song song với nhau thì mọi đường thẳng nằm trong mặt phẳng đều song song với (II) Hai đường thẳng nằm trên hai mặt phẳng song song thì song song với nhau.
(III) Trong không gian hai đường thẳng không có điểm chung thì chéo nhau. (IV) Có thể tìm được hai đường thẳng song song mà mỗi đường thẳng cắt đồng thời hai đường thẳng chéo nhau cho trước.
Trong các mệnh đề trên có bao nhiêu mệnh đề sai?
 Xem đáp án
Xem đáp án
Có 3 mệnh đề sai là (II), (III), (IV).
(II) sai vì hai đường thẳng nằm trên hai mặt
phẳng song song thì có thể song song hoặc chéo nhau.
(III) sai vì hai đường thẳng không có điểm chung
thì có thể chéo nhau hoặc song song với nhau.
(IV) sai vì nếu tồn tại hai đường song song mà
mỗi đường thẳng cắt đồng thời hai đường thẳng
chéo nhau cho trước thì cả bốn đường đó sẽ đồng
phẳng (mâu thuẫn với dữ kiện hai đường thẳng ban đầu chéo nhau).
Đáp án cần chọn là: D
Câu 12:
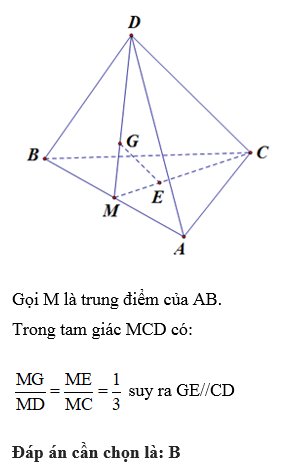
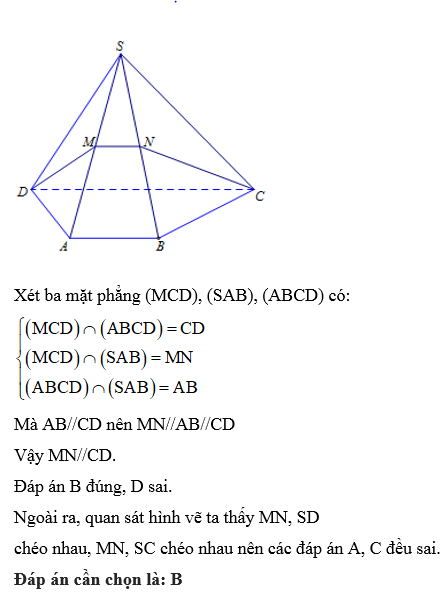
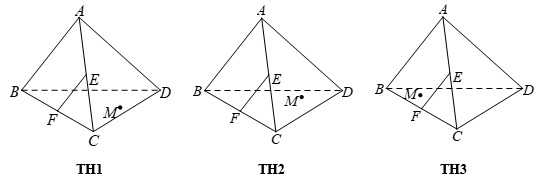
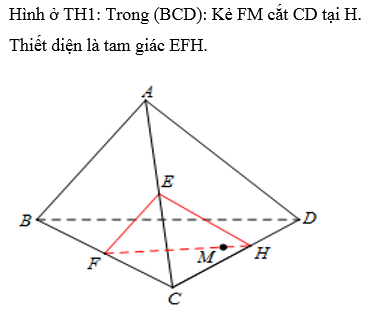
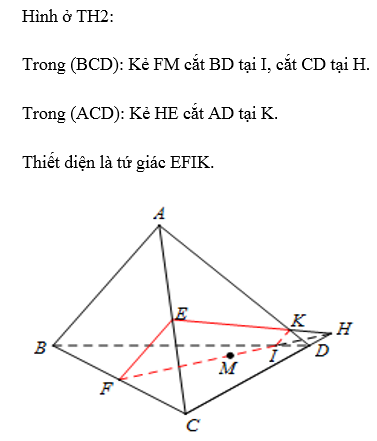
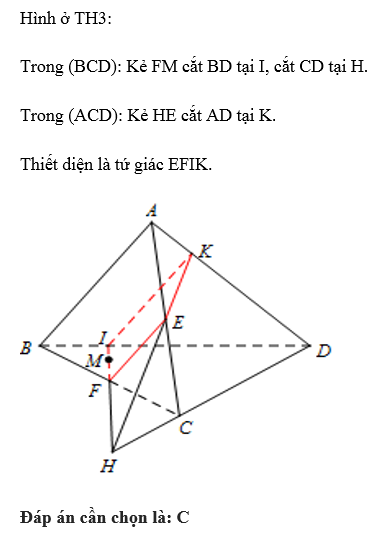
Cho tứ diện ABCD. Gọi M là một điểm bất kì nằm trên đoạn AC (khác A và C). Mặt phẳng (P) qua M và song song với các đường thẳng AB, CD. Thiết diện của (P) với tứ diện đã cho là hình gì?
 Xem đáp án
Xem đáp án
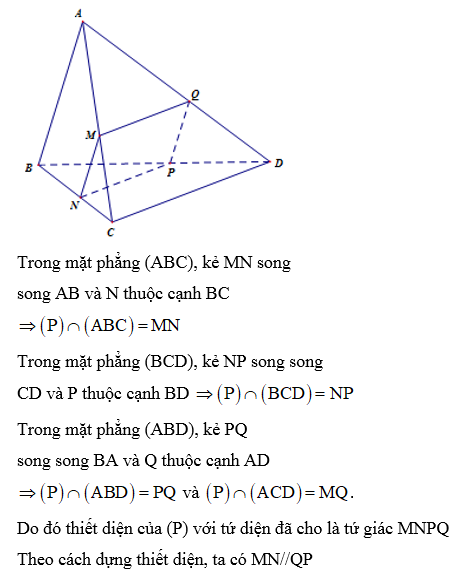
Đáp án cần chọn là: B
Câu 17:
Hai mặt phẳng song song có bao nhiêu mặt phẳng đối xứng?
 Xem đáp án
Xem đáp án
Do mặt phẳng không có bề dày và không có giới hạn
nên hai mặt phẳng song song có một mặt phẳng đối
xứng là mặt phẳng nằm cách đều hai mặt phẳng
song song đó và có vô số mặt phẳng đối xứng khác
là các mặt phẳng vuông góc với hai mặt phẳng đã cho.
Đáp án cần chọn là: D