Giải SGK Toán 11 Cánh diều Góc lượng giác. Giá trị lượng giác của góc lượng giác có đáp án
Giải SGK Toán 11 Cánh diều Góc lượng giác. Giá trị lượng giác của góc lượng giác có đáp án
-
536 lượt thi
-
42 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Trên mặt chiếc đồng hồ, kim giây đang ở vị trí ban đầu chỉ vào số 3 (Hình 1). Kim giây quay ba vòng và một phần tư vòng (tức là \(3\frac{1}{4}\) vòng) đến vị trí cuối chỉ vào số 6. Khi quay như thế, kim giây đã quét một góc với tia đầu chỉ vào số 3, tia cuối chỉ vào số 6.

Góc đó gợi nên khái niệm gì trong toán học? Những góc như thế có tính chất gì?
 Xem đáp án
Xem đáp án
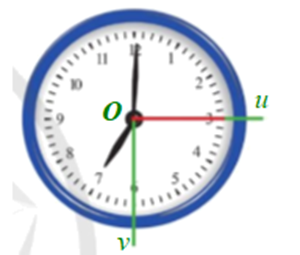
Kim giây đã quét một góc với tia đầu Ou chỉ vào số 3, tia cuối Ov chỉ vào số 6 (hình vẽ trên), góc này là một góc lượng giác.
Những góc lượng giác có cùng tia đầu và tia cuối thì có số đo hơn kém nhau k360° (hay k2π).
Câu 2:
Nêu định nghĩa góc trong hình học phẳng.
 Xem đáp án
Xem đáp án
Góc (còn được gọi là góc hình học) là hình gồm hai tia chung gốc. Mỗi góc có một số đo, đơn vị đo góc (hình học) là độ. Số đo của một góc (hình học) không vượt quá 180°.
Chẳng hạn: Góc xOy gồm hai tia Ox và Oy chung gốc O có số đo là 60° (hình vẽ).
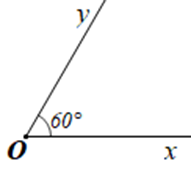
Câu 3:
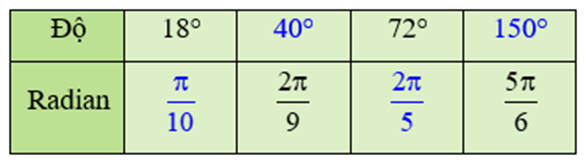
Hãy hoàn thành bảng chuyển đổi số đo độ và số đo radian của một số góc sau.

 Xem đáp án
Xem đáp án
Ta có: \(18^\circ = 18.\frac{\pi }{{180}} = \frac{\pi }{{10}}\); \(72^\circ = 72.\frac{\pi }{{180}} = \frac{{2\pi }}{5}\);
\[\frac{{2\pi }}{9} = {\left( {\frac{{2\pi }}{9}.\frac{{180}}{\pi }} \right)^o} = 40^\circ \]; \[\frac{{5\pi }}{6} = {\left( {\frac{{5\pi }}{6}.\frac{{180}}{\pi }} \right)^o} = 150^\circ \]
Ta có bảng chuyển đổi như sau:
Câu 4:
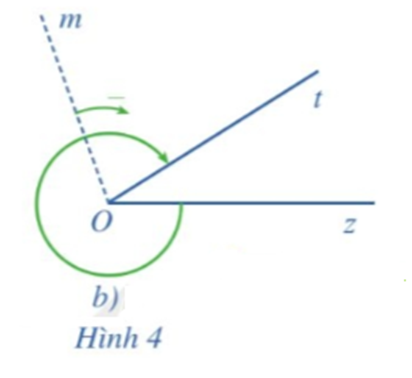
Đọc tên góc lượng giác, tia đầu và tia cuối của góc lượng giác đó trong Hình 4b.
 Xem đáp án
Xem đáp án
Trong Hình 4b, góc lượng giác là (Oz, Ot) với tia đầu Oz và tia cuối Ot.
Câu 5:
So sánh chiều quay của kim đồng hồ với:
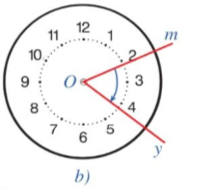
Chiều quay từ tia Om đến tia Oy trong Hình 3b.
 Xem đáp án
Xem đáp án
Chiều quay của kim đồng hồ cùng chiều với chiều quay từ tia Om đến tia Oy trong Hình 3b.
Câu 6:
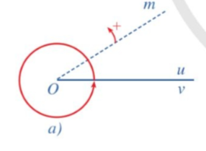
Trong Hình 5a, tia Om quay theo chiều dương đúng một vòng. Hỏi tia đó quét nên một góc bao nhiêu độ?
 Xem đáp án
Xem đáp án
Trong Hình 5a, tia Om quay theo chiều dương đúng một vòng thì tia đó quét nên một góc 360°.
Câu 7:
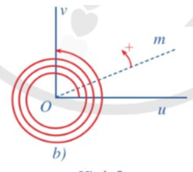
Trong Hình 5b, tia Om quay theo chiều dương ba vòng và một phần tư vòng (tức là \(3\frac{1}{4}\) vòng). Hỏi tia đó quét nên một góc bao nhiêu độ?
 Xem đáp án
Xem đáp án
Trong Hình 5b, tia Om quay theo chiều dương ba vòng và một phần tư vòng (tức là \(3\frac{1}{4}\) vòng) thì tia đó quét nên một góc là \(3\frac{1}{4}.360^\circ = 1\,\,170^\circ \).
Câu 8:
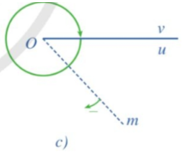
Trong Hình 5c, tia Om quay theo chiều âm đúng một vòng. Hỏi tia đó quét nên một góc bao nhiêu độ?
 Xem đáp án
Xem đáp án
Trong Hình 5c, tia Om quay theo chiều âm đúng một vòng thì tia đó quét nên một góc là ‒360°.
Câu 9:
Hãy biểu diễn trên mặt phẳng góc lượng giác gốc O có tia đầu Ou, tia cuối Ov và có số đo \( - \frac{{5\pi }}{4}\).
 Xem đáp án
Xem đáp án
Ta có: \( - \frac{{5\pi }}{4} = - \pi + \left( { - \frac{\pi }{4}} \right)\).
Góc lượng giác gốc O có tia đầu Ou, tia cuối Ov và có số đo \( - \frac{{5\pi }}{4}\) được biểu diễn ở hình vẽ dưới đây:

Câu 10:
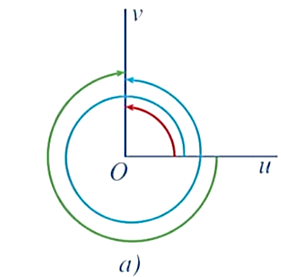
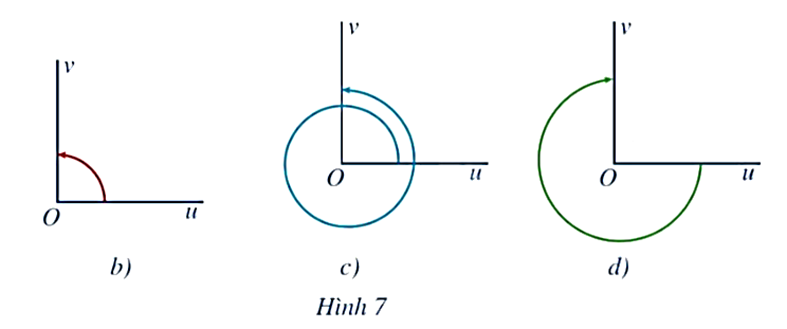
Trong Hình 7a, ba góc lượng giác có cùng tia đầu Ou và tia cuối Ov, trong đó Ou ⊥ Ov. Xác định số đo của góc lượng giác trong các Hình 7b, 7c, 7d.
 Xem đáp án
Xem đáp án
Quan sát Hình 7 ta thấy:
+ Số đo của góc lượng giác có tia đầu Ou và tia cuối Ov trong Hình 7b) là 90°.
+ Số đo của góc lượng giác có tia đầu Ou và tia cuối Ov trong Hình 7c) là 360° + 90° = 450°.
+ Số đo của góc lượng giác có tia đầu Ou và tia cuối Ov trong Hình 7d) là – (360° – 90°) = 90° – 360° = 270°.
Câu 11:
 Xem đáp án
Xem đáp án
Câu 12:
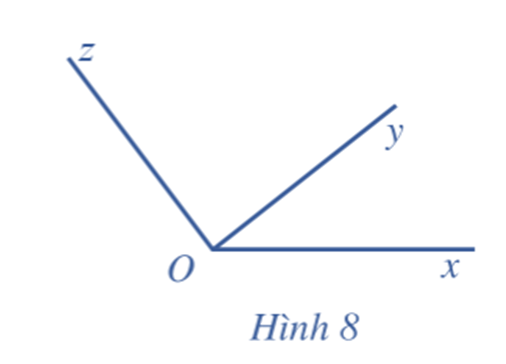
Cho góc (hình học) xOz, tia Oy nằm trong góc xOz (Hình 8). Nêu mối liên hệ giữa số đo của góc xOz và tổng số đo của hai góc xOy và yOz.
 Xem đáp án
Xem đáp án
Do tia Oy nằm trong góc xOz nên \(\widehat {xOz} = \widehat {xOy} + \widehat {yOz}\).
Câu 13:
Cho góc lượng giác (Ou, Ov) có số đo là \( - \frac{{11\pi }}{4}\), góc lượng giác (Ou, Ow) có số đo là \(\frac{{3\pi }}{4}.\) Tìm số đo của góc lượng giác (Ov, Ow).
 Xem đáp án
Xem đáp án
Theo hệ thức Chasles, ta có:
(Ov, Ow) = (Ou, Ow) – (Ou, Ov) + k2π
\( = \frac{{3\pi }}{4} - \left( { - \frac{{11\pi }}{4}} \right) + k2\pi = \frac{{7\pi }}{2} + k2\pi \) (k ∈ ℤ).
Câu 14:
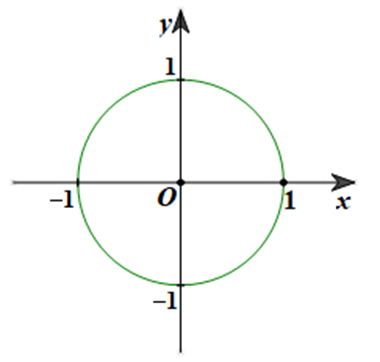
Trong mặt phẳng toạ độ (định hướng) Oxy, hãy vẽ đường tròn tâm O với bán kính bằng 1.
 Xem đáp án
Xem đáp án
Đường tròn tâm O có bán kính bằng 1 (hình vẽ):
Câu 15:
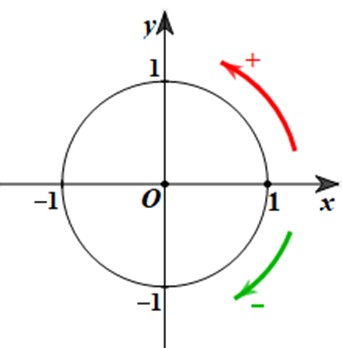
Hãy nêu chiều dương, chiều âm trên đường tròn tâm O với bán kính bằng 1.
 Xem đáp án
Xem đáp án
Chiều dương là chiều ngược với chiều quay của kim đồng hồ; chiều âm là chiều quay của kim đồng hồ.
Câu 16:
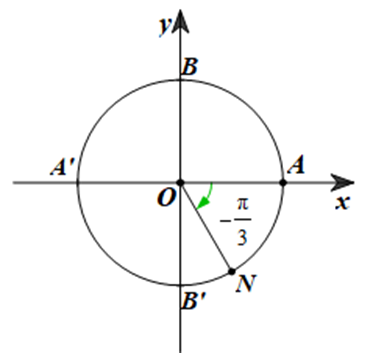
Xác định điểm N trên đường tròn lượng giác sao cho (OA, ON) = \( - \frac{\pi }{3}\).
 Xem đáp án
Xem đáp án
Ta có (OA, ON) = \( - \frac{\pi }{3}\) là góc lượng giác có tia đầu là tia OA, tia cuối là tia ON và quay theo chiều âm (chiều quay của kim đồng hồ) một góc \(\frac{\pi }{3}\).
Điểm N trên đường tròn lượng giác sao cho (OA, ON) = \( - \frac{\pi }{3}\) được biểu diễn như hình dưới đây:
Câu 17:
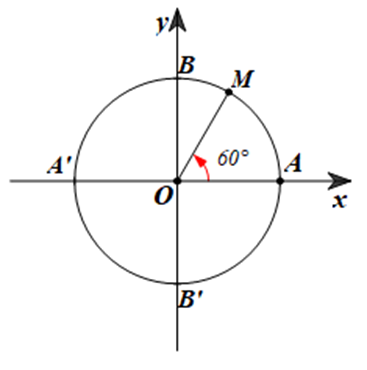
Xác định điểm M trên đường tròn lượng giác sao cho (OA, OM) = 60°.
 Xem đáp án
Xem đáp án
Ta có (OA, OM) = 60° là góc lượng giác có tia đầu là tia OA, tia cuối là tia OM và quay theo chiều dương một góc 60°.
Điểm M trên đường tròn lượng giác sao cho (OA, OM) = 60° được biểu diễn như hình vẽ dưới đây:
Câu 18:
Tìm giá trị lượng giác của góc lượng giác \(\beta = - \frac{\pi }{4}\).
 Xem đáp án
Xem đáp án
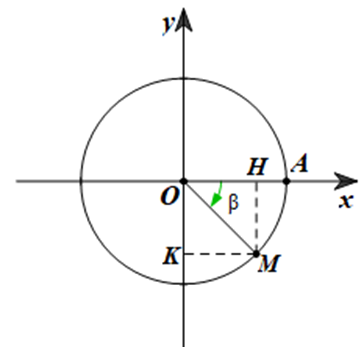
Lấy điểm M trên đường tròn lượng giác sao cho (OA, OM) = β = \( - \frac{\pi }{4} = - {\rm{45}}^\circ \) (hình vẽ).
Gọi H, K lần lượt là hình chiếu của điểm M trên các trục Ox, Oy.
Khi đó, ta có: \(\widehat {AOM} = {\rm{45}}^\circ \), suy ra \(\widehat {HOM} = \widehat {AOM} = {\rm{45}}^\circ \).
Theo hệ thức trong tam giác vuông HOM, ta có:
\(OH = OM.cos\widehat {HOM} = 1.c{\rm{os45}}^\circ = \frac{{\sqrt 2 }}{2}\);
\(OK = MH = OM.\sin \widehat {HOM} = 1.\sin {\rm{45}}^\circ = \frac{{\sqrt 2 }}{2}\).
Do đó \(M\left( {\frac{{\sqrt 2 }}{2}; - \frac{{\sqrt 2 }}{2}} \right)\).
Vậy \[\sin \left( { - \frac{\pi }{4}} \right) = - \frac{{\sqrt 2 }}{2};cos\left( { - \frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2};\]\(\tan \left( { - \frac{\pi }{4}} \right) = - 1;\cot \left( { - \frac{\pi }{4}} \right) = - 1\).
Câu 19:
Xét dấu các giá trị lượng giác của góc lượng giác α = ‒ 30°.
 Xem đáp án
Xem đáp án
Giả sử M là một điểm trên đường tròn lượng giác sao cho (OA, OM) = α = ‒ 30°.
Điểm M được biểu diễn như hình vẽ sau:
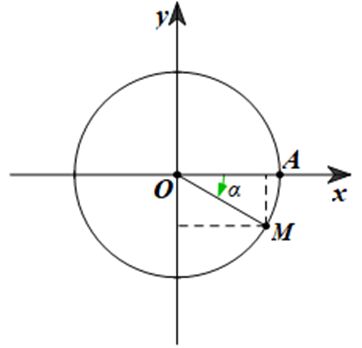
Khi đó ta có xM > 0 và yM < 0
Suy ra cosα > 0 và sinα < 0
Do đó \(\tan \alpha = \frac{{\sin \alpha }}{{cos\alpha }} < 0\) và \(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} < 0\).
Câu 20:
Xét dấu các giá trị lượng giác của góc lượng giác \(\alpha = \frac{{5\pi }}{6}\).
 Xem đáp án
Xem đáp án
Do \(\frac{\pi }{2} < \frac{{5\pi }}{6} < \pi \) nên \(\sin \frac{{5\pi }}{6} > 0 & ;\,\,cos\frac{{5\pi }}{6} < 0;\,\,\tan \frac{{5\pi }}{6} < 0;\,\,\cot \frac{{5\pi }}{6} < 0\).
Câu 21:
Cho góc lượng giác α. So sánh:
tanα . cotα và 1 (với cosα ≠ 0, sinα ≠ 0)
 Xem đáp án
Xem đáp án
Ta có \[\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\], \(\cot \alpha = \frac{{cos\alpha }}{{\sin \alpha }}\) (với cosα ≠ 0, sinα ≠ 0)
Suy ra \(\tan \alpha .\cot \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}.\frac{{\cos \alpha }}{{\sin \alpha }} = 1\).
Câu 22:
Cho góc lượng giác alpha. So sánh:
\[1 + {\tan ^2}\alpha \] và \(\frac{1}{{co{s^2}\alpha }}\) với cosα ≠ 0
 Xem đáp án
Xem đáp án
Với cosα ≠ 0, ta có:
\[1 + {\tan ^2}\alpha = 1 + {\left( {\frac{{\sin \alpha }}{{\cos \alpha }}} \right)^2} = \frac{{{{\cos }^2}\alpha + {{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{1}{{{{\cos }^2}\alpha }}\] (do cos2α + sin2α = 1).
Câu 23:
Cho góc lượng giác alpha. So sánh:
\(1 + {\cot ^2}\alpha \) và \(\frac{1}{{{{\sin }^2}\alpha }}\) với sinα ≠ 0
 Xem đáp án
Xem đáp án
Với sinα ≠ 0, ta có:
\[1 + {\cot ^2}\alpha = 1 + {\left( {\frac{{\cos \alpha }}{{\sin \alpha }}} \right)^2} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{1}{{{{\sin }^2}\alpha }}\] (do cos2α + sin2α = 1).
Câu 24:
Cho góc lượng giác α sao cho \(\pi < \alpha < \frac{{3\pi }}{2}\) và \(\sin \alpha = - \frac{4}{5}\). Tìm cosα.
 Xem đáp án
Xem đáp án
Do \(\pi < \alpha < \frac{{3\pi }}{2}\) nên cosα < 0.
Áp dụng công thức cos2α + sin2α = 1, ta có: \[co{s^2}\alpha + {\left( { - \frac{4}{5}} \right)^2} = 1\]
Suy ra \[co{s^2}\alpha = 1 - {\left( { - \frac{4}{5}} \right)^2} = 1 - \frac{{16}}{{25}} = \frac{9}{{25}}\]
Do đó \[cos\alpha = - \frac{3}{5}\] (do cosα < 0).
Câu 25:
Tìm các giá trị lượng giác của góc lượng giác \(\alpha = \frac{\pi }{4}\).
 Xem đáp án
Xem đáp án
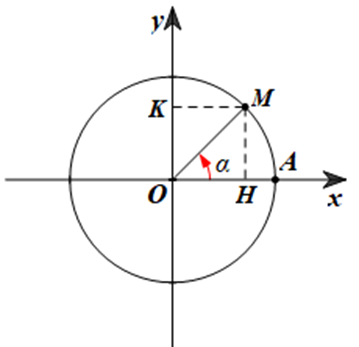
Lấy điểm M trên đường tròn lượng giác sao cho (OA, OM) = \(\alpha = \frac{\pi }{4} = 45^\circ \) (hình vẽ).
Gọi H, K lần lượt là hình chiếu của điểm M trên các trục Ox, Oy.
Khi đó, ta có: \(\widehat {AOM} = {\rm{45}}^\circ \).
Theo hệ thức trong tam giác vuông HOM, ta có:
\({x_M} = OH = OM.cos\widehat {HOM} = 1.c{\rm{os45}}^\circ = \frac{{\sqrt 2 }}{2}\);
\({y_M} = OK = MH = OM.\sin \widehat {HOM} = 1.\sin {\rm{45}}^\circ = \frac{{\sqrt 2 }}{2}\).
Do đó \(M\left( {\frac{{\sqrt 2 }}{2};\frac{{\sqrt 2 }}{2}} \right)\).
Vậy \[\sin 45^\circ = \frac{{\sqrt 2 }}{2};cos45^\circ = \frac{{\sqrt 2 }}{2};\]\(\tan 45^\circ = 1;\cot 45^\circ = 1\).
Câu 26:
Tính giá trị của biểu thức: \(Q = {\tan ^2}\frac{\pi }{3} + {\sin ^2}\frac{\pi }{4} + \cot \frac{\pi }{4} + cos\frac{\pi }{2}\).
 Xem đáp án
Xem đáp án
Ta có:
\(Q = {\tan ^2}\frac{\pi }{3} + {\sin ^2}\frac{\pi }{4} + \cot \frac{\pi }{4} + cos\frac{\pi }{2}\)
\( = {\left( {\sqrt 3 } \right)^2} + {\left( {\frac{{\sqrt 2 }}{2}} \right)^2} + 1 + 0 = 3 + \frac{1}{2} + 1 = \frac{9}{2}\).
Câu 27:
Trên đường tròn lượng giác, cho hai điểm M, M’ sao cho góc lượng giác (OA, OM) = α, góc lượng giác (OA, OM’) = – α (Hình 13).
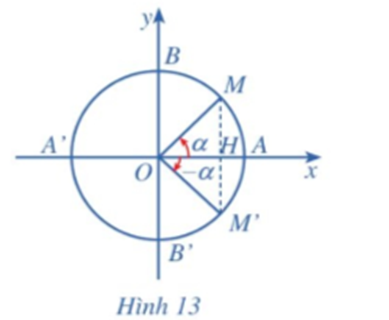
a) Đối với hai điểm M, M’ nêu nhận xét về: hoành độ của chúng, tung độ của chúng.
b) Nêu mối liên hệ giữa các giá trị lượng giác tương ứng của hai góc lượng giác α và – α. Xem đáp án
Xem đáp án
a) Nhận xét: xM = xM’ và yM = ‒yM’.
b) Do xM = xM’ nên cosα = cos(‒α)
Do yM = ‒yM’ nên sinα = ‒sin(‒α).
Khi đó \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{ - \sin \left( { - \alpha } \right)}}{{\cos \left( { - \alpha } \right)}} = - \tan \left( { - \alpha } \right)\);
\(\cot \alpha = \frac{1}{{\tan \alpha }} = \frac{1}{{ - \tan \left( { - \alpha } \right)}} = - \cot \left( { - \alpha } \right)\).
Câu 28:
Tính:
\(co{s^2}\frac{\pi }{8} + co{s^2}\frac{{3\pi }}{8}\)
 Xem đáp án
Xem đáp án
Ta có:
\(co{s^2}\frac{\pi }{8} + co{s^2}\frac{{3\pi }}{8} = co{s^2}\frac{\pi }{8} + {\sin ^2}\left( {\frac{\pi }{2} - \frac{{3\pi }}{8}} \right)\)
\( = co{s^2}\frac{\pi }{8} + {\sin ^2}\frac{\pi }{8} = 1\).
Câu 29:
Tính:
tan1° . tan2° . tan45° . tan88° . tan89°.
 Xem đáp án
Xem đáp án
Ta có:
tan1° . tan2° . tan45° . tan88° . tan89°
= (tan1° . tan89°) . (tan2° . tan88°) . tan45°
= (tan1° . cot1°) . (tan2° . cot2°) . tan45°
= 1 . 1 . 1 = 1.
Câu 30:
Dùng máy tính cầm tay để tính:
a) tan(‒75°);
b) \(\cot \left( { - \frac{\pi }{5}} \right)\).
 Xem đáp án
Xem đáp án
a) Chuyển máy tính về chế độ “độ”:

b) Ta có: \(\cot \left( { - \frac{\pi }{5}} \right) = \frac{1}{{\tan \left( { - \frac{\pi }{5}} \right)}}\)
Chuyển máy tính về chế độ “radian”.
|
Phép tính |
Nút ấn |
Kết quả |
|
\(\cot \left( { - \frac{\pi }{5}} \right)\) |
|
– 1.37638192 |
Vậy \(\cot \left( { - \frac{\pi }{5}} \right) = - 1,37638192\).
Câu 31:
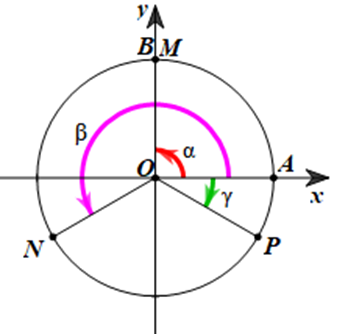
Xác định vị trí các điểm M, N, P trên đường tròn lượng giác sao cho số đo của các góc lượng giác (OA, OM), (OA, ON), (OA, OP) lần lượt bằng \(\frac{\pi }{2};\frac{{7\pi }}{6}; - \frac{\pi }{6}\).
 Xem đáp án
Xem đáp án
• Ta có \(\left( {OA,OM} \right) = \alpha = \frac{\pi }{2}\) là góc lượng giác có tia đầu là tia OA, tia cuối là tia OM và quay theo chiều dương một góc \(\frac{\pi }{2}\), khi đó tia OM trùng với tia OB.
Điểm M trên đường tròn lượng giác sao cho \(\left( {OA,OM} \right) = \alpha = \frac{\pi }{2}\) được biểu diễn trùng với điểm B.
• Ta có \[\left( {OA,ON} \right) = \beta = \frac{{7\pi }}{6} = \pi + \frac{\pi }{6}\] là góc lượng giác có tia đầu là tia OA, tia cuối là tia ON và quay theo chiều dương một góc \[\frac{{7\pi }}{6}\].
• Ta có \[\left( {OA,OP} \right) = \gamma = - \frac{\pi }{6}\] là góc lượng giác có tia đầu là tia OA, tia cuối là tia OP và quay theo chiều âm một góc \[\frac{\pi }{6}\].
Ba điểm M, N, P trên đường tròn lượng giác được biểu diễn như hình vẽ dưới đây:
Câu 32:
Tính các giá trị lượng giác của mỗi góc sau: 225°; ‒225°; ‒1 035°; \(\frac{{5\pi }}{3};\frac{{19\pi }}{2}; - \frac{{159\pi }}{4}\).
 Xem đáp án
Xem đáp án
‒ Các giá trị lượng giác của góc 225°:
Ta có: cos225° = cos(45° + 180°)= ‒cos45° = \( - \frac{{\sqrt 2 }}{2}\);
sin225° = sin(45° + 180°) = ‒sin45° = \( = - \frac{{\sqrt 2 }}{2}\);
tan225° = tan(45° + 180°) = tan45° = 1;
cot225° = cot(45° + 180°) = cot45° = 1.
‒ Các giá trị lượng giác của góc ‒225°:
Ta có: cos(‒225°) = cos225° = \( - \frac{{\sqrt 2 }}{2}\);
sin(‒225°) = ‒sin225° = \[ - \left( { - \frac{{\sqrt 2 }}{2}} \right) = \frac{{\sqrt 2 }}{2}\];
tan(‒225°) = ‒tan225° = ‒1;
cot(‒225°) = ‒cot225° = ‒1;
‒ Các giá trị lượng giác của góc ‒1 035°:
Ta có: cos(‒1 035°) = cos(‒3 . 360° + 45°) = cos45° = \(\frac{{\sqrt 2 }}{2}\);
sin(‒1 035°) = sin(‒3 . 360° + 45°) = sin45° = \(\frac{{\sqrt 2 }}{2}\);
tan(‒1 035°) = tan(‒3 . 360° + 45°) = tan45° = 1;
cot(‒1 035°) = cot(‒3 . 360° + 45°) = cot45° = 1.
‒ Các giá trị lượng giác của góc \(\frac{{5\pi }}{3}\):
Ta có: \(cos\frac{{5\pi }}{3} = cos\left( {\frac{{2\pi }}{3} + \pi } \right) = - cos\frac{{2\pi }}{3} = - \left( { - \frac{1}{2}} \right) = \frac{1}{2}\);
\[\sin \frac{{5\pi }}{3} = \sin \left( {\frac{{2\pi }}{3} + \pi } \right) = - \sin \frac{{2\pi }}{3} = - \frac{{\sqrt 3 }}{2}\];
\[\tan \frac{{5\pi }}{3} = \tan \left( {\frac{{2\pi }}{3} + \pi } \right) = \tan \frac{{2\pi }}{3} = - \sqrt 3 \];
\[\cot \frac{{5\pi }}{3} = \cot \left( {\frac{{2\pi }}{3} + \pi } \right) = \cot \frac{{2\pi }}{3} = - \frac{{\sqrt 3 }}{3}\].
‒ Các giá trị lượng giác của góc \(\frac{{19\pi }}{2}\):
Ta có: \(cos\frac{{19\pi }}{2} = cos\left( {9\pi + \frac{\pi }{2}} \right) = c{\rm{os}}\left( {\pi + \frac{\pi }{2}} \right) = - cos\frac{\pi }{2} = 0\);
\(\sin \frac{{19\pi }}{2} = \sin \left( {9\pi + \frac{\pi }{2}} \right) = \sin \left( {\pi + \frac{\pi }{2}} \right) = - \sin \frac{\pi }{2} = - 1\);
Do \(cos\frac{{19\pi }}{2} = 0\) nên \(\tan \frac{{19\pi }}{2}\) không xác định;
\(\cot \frac{{19\pi }}{2} = \cot \left( {9\pi + \frac{\pi }{2}} \right) = \cot \left( {\pi + \frac{\pi }{2}} \right) = \cot \frac{\pi }{2} = 0\).
‒ Các giá trị lượng giác của góc \( - \frac{{159\pi }}{4}\):
Ta có: \[cos\left( { - \frac{{159\pi }}{4}} \right) = cos\left( { - 40\pi + \frac{\pi }{4}} \right) = c{\rm{os}}\frac{\pi }{4} = \frac{{\sqrt 2 }}{2}\];
\[\sin \left( { - \frac{{159\pi }}{4}} \right) = \sin \left( { - 40\pi + \frac{\pi }{4}} \right) = {\rm{sin}}\frac{\pi }{4} = \frac{{\sqrt 2 }}{2}\];
\[\tan \left( { - \frac{{159\pi }}{4}} \right) = \tan \left( { - 40\pi + \frac{\pi }{4}} \right) = \tan \frac{\pi }{4} = 1\];
\[\cot \left( { - \frac{{159\pi }}{4}} \right) = \cot \left( { - 40\pi + \frac{\pi }{4}} \right) = \cot \frac{\pi }{4} = 1\].
Câu 33:
Tính các giá trị lượng giác (nếu có) của mỗi góc sau:
\(\frac{\pi }{3} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\);
 Xem đáp án
Xem đáp án
Các giá trị lượng giác của góc lượng giác \(\frac{\pi }{3} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\):
• \(cos\left( {\frac{\pi }{3} + k2\pi \,} \right) = cos\frac{\pi }{3} = \frac{1}{2}\);
• \(\sin \left( {\frac{\pi }{3} + k2\pi \,} \right) = \sin \frac{\pi }{3} = \frac{{\sqrt 3 }}{2}\);
• \(\tan \left( {\frac{\pi }{3} + k2\pi \,} \right) = \tan \frac{\pi }{3} = \sqrt 3 \);
• \(\cot \left( {\frac{\pi }{3} + k2\pi \,} \right) = \cot \frac{\pi }{3} = \frac{{\sqrt 3 }}{3}\).
Câu 34:
Tính các giá trị lượng giác (nếu có) của mỗi góc sau:
\(\frac{\pi }{3} + \left( {2k + 1} \right)\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
 Xem đáp án
Xem đáp án
Các giá trị lượng giác của góc lượng giác \(\frac{\pi }{3} + \left( {2k + 1} \right)\pi \,\,\left( {k \in \mathbb{Z}} \right)\):
• \(cos\left[ {\frac{\pi }{3} + \left( {2k + 1} \right)\pi } \right] = \cos \left( {\frac{\pi }{3} + \pi + 2k\pi } \right) = \cos \left( {\frac{\pi }{3} + \pi } \right) = - cos\frac{\pi }{3} = - \frac{1}{2}\);
• \(\sin \left[ {\frac{\pi }{3} + \left( {2k + 1} \right)\pi } \right] = \sin \left( {\frac{\pi }{3} + \pi + 2k\pi } \right) = \sin \left( {\frac{\pi }{3} + \pi } \right) = - \sin \frac{\pi }{3} = - \frac{{\sqrt 3 }}{2}\);
• \(\tan \left[ {\frac{\pi }{3} + \left( {2k + 1} \right)\pi } \right] = \tan \frac{\pi }{3} = \sqrt 3 \);
• \(\tan \left[ {\frac{\pi }{3} + \left( {2k + 1} \right)\pi } \right] = \cot \frac{\pi }{3} = \frac{{\sqrt 3 }}{3}\).
Câu 35:
Tính các giá trị lượng giác (nếu có) của mỗi góc sau:
kπ (k ∈ ℤ);
 Xem đáp án
Xem đáp án
Các giá trị lượng giác của góc lượng giác kπ (k ∈ ℤ):
‒ Nếu k là số chẵn, tức k = 2n (n ∈ ℤ) thì kπ = 2nπ, ta có:
• cos(kπ) = cos(2nπ) = cos0 = 1;
• sin(kπ) = sin(2nπ) = sin0 = 0;
• tan(kπ) = tan(2nπ) = tan0 = 0;
• Do sin(kπ) = 0 nên cot(kπ) không xác định.
‒ Nếu k là số lẻ, tức k = 2n + 1 (n ∈ ℤ) thì kπ = (2n + 1)π = 2nπ + π, ta có:
• cos(kπ) = cos(2nπ + π) = cosπ = ‒1.
• sin(kπ) = sin(2nπ + π) = sinπ = 0.
• tan(kπ) = tan(2nπ + π) = tanπ = 0.
• Do sin(kπ) = 0 nên cot(kπ) không xác định.
Vậy với k ∈ ℤ thì sin(kπ) = 0; tan(kπ) = 0; cot(kπ) không xác định;
cos(kπ) = 1 khi k là số nguyên chẵn và cos(kπ) = ‒1 khi k là số nguyên lẻ.
Câu 36:
Tính các giá trị lượng giác (nếu có) của mỗi góc sau:
\(\frac{\pi }{2} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\);
 Xem đáp án
Xem đáp án
Các giá trị lượng giác của góc lượng giác \(\frac{\pi }{2} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\):
‒ Nếu k là số chẵn, tức k = 2n (n ∈ ℤ) thì kπ = 2nπ, ta có:
• \(cos\left( {\frac{\pi }{2} + k\pi \,} \right) = cos\left( {\frac{\pi }{2} + 2n\pi \,} \right) = cos\frac{\pi }{2} = 0\);
• \(\sin \left( {\frac{\pi }{2} + k\pi \,} \right) = \sin \left( {\frac{\pi }{2} + 2n\pi \,} \right) = \sin \frac{\pi }{2} = 1\);
• Do \(cos\left( {\frac{\pi }{2} + k\pi \,} \right) = 0\) nên \(\tan \left( {\frac{\pi }{2} + k\pi \,} \right)\) không xác định;
• \(\cot \left( {\frac{\pi }{2} + k\pi \,} \right) = \cot \left( {\frac{\pi }{2} + 2n\pi \,} \right) = \cot \frac{\pi }{2} = 0\).
‒ Nếu k là số lẻ, tức k = 2n + 1 (n ∈ ℤ) thì kπ = (2n + 1)π = 2nπ + π, ta có:
• \(cos\left( {\frac{\pi }{2} + k\pi \,} \right) = cos\left( {\frac{\pi }{2} + 2n\pi \, + \pi } \right) = cos\left( {\frac{\pi }{2}\, + \pi } \right) = - cos\frac{\pi }{2} = 0\);
• \[\sin \left( {\frac{\pi }{2} + k\pi \,} \right) = \sin \left( {\frac{\pi }{2} + 2n\pi \, + \pi } \right) = \sin \left( {\frac{\pi }{2} + \pi } \right) = - \sin \frac{\pi }{2} = - 1\];
• Do \(cos\left( {\frac{\pi }{2} + k\pi \,} \right) = 0\) nên \(\tan \left( {\frac{\pi }{2} + k\pi \,} \right)\) không xác định;
• \(\cot \left( {\frac{\pi }{2} + k\pi \,} \right) = \cot \left( {\frac{\pi }{2} + 2n\pi \, + \pi } \right) = \cot \left( {\frac{\pi }{2}\, + \pi } \right) = \cot \frac{\pi }{2} = 0\).
Vậy với k ∈ ℤ thì \(cos\left( {\frac{\pi }{2} + k\pi \,} \right) = 0\); \(\cot \left( {\frac{\pi }{2} + k\pi \,} \right) = 0\);
\(\tan \left( {\frac{\pi }{2} + k\pi \,} \right)\) không xác định;
\[\sin \left( {\frac{\pi }{2} + k\pi \,} \right) = 1\] khi k là số chẵn và \[\sin \left( {\frac{\pi }{2} + k\pi \,} \right) = - 1\] khi k là số lẻ.
Câu 37:
Tính các giá trị lượng giác của góc alpha trong mỗi trường hợp sau:
\(\sin \alpha = \frac{{\sqrt {15} }}{4}\) với \(\frac{\pi }{2} < \alpha < \pi \)
 Xem đáp án
Xem đáp án
Do \(\frac{\pi }{2} < \alpha < \pi \) nên cosα < 0.
Áp dụng công thức sin2α + cos2α = 1, ta có:
\[{\left( {\frac{{\sqrt {15} }}{4}} \right)^2} + co{s^2}\alpha = 1\]
\[ \Rightarrow co{s^2}\alpha = 1 - {\left( {\frac{{\sqrt {15} }}{4}} \right)^2} = 1 - \frac{{15}}{{16}} = \frac{1}{{16}}\]
\[ \Rightarrow cos\alpha = - \frac{1}{4}\] (do cosα < 0).
Ta có: \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{\frac{{\sqrt {15} }}{4}}}{{ - \frac{1}{4}}} = - \sqrt {15} \);
\(\cot \alpha = \frac{1}{{\tan \alpha }} = \frac{1}{{ - \sqrt {15} }} = - \frac{{\sqrt {15} }}{{15}}\).
Vậy \[cos\alpha = - \frac{1}{4}\]; \(\tan \alpha = - \sqrt {15} \) và \(\cot \alpha = - \frac{{\sqrt {15} }}{{15}}\).
Câu 38:
Tính các giá trị lượng giác của góc alpha trong mỗi trường hợp sau:
\(cos\alpha = - \frac{2}{3}\) với \( - \pi < \alpha < 0\)
 Xem đáp án
Xem đáp án
Do ‒π < α < 0 nên sinα < 0.
Áp dụng công thức sin2α + cos2α = 1, ta có:
\[{\sin ^2}\alpha + {\left( { - \frac{2}{3}} \right)^2} = 1\]
\[ \Rightarrow {\sin ^2}\alpha = 1 - {\left( { - \frac{2}{3}} \right)^2} = 1 - \frac{4}{9} = \frac{5}{9}\].
\( \Rightarrow \sin \alpha = - \frac{{\sqrt 5 }}{3}\) (do sinα < 0).
Ta có: \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{ - \frac{{\sqrt 5 }}{3}}}{{ - \frac{2}{3}}}\)\( = \frac{{\sqrt 5 }}{2}\);
\(\cot \alpha = \frac{1}{{\tan \alpha }} = \frac{1}{{\frac{{\sqrt 5 }}{2}}} = \frac{2}{{\sqrt 5 }} = \frac{{2\sqrt 5 }}{5}\).
Vậy \(\sin \alpha = - \frac{{\sqrt 5 }}{3}\); \(\tan \alpha = \frac{{\sqrt 5 }}{2}\) và \(\cot \alpha = \frac{{2\sqrt 5 }}{5}\).
Câu 39:
Tính các giá trị lượng giác của góc alpha trong trường hợp sau:
tanα = 3 với ‒π < α < 0
 Xem đáp án
Xem đáp án
Do ‒π < α < 0 nên sinα < 0 và cosα > 0 khi \( - \frac{\pi }{2} \le \alpha < 0\), cosα < 0 khi \( - \pi < \alpha < - \frac{\pi }{2}\).
Mà tanα = 3 > 0, do đó \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} > 0\), từ đó suy ra cosα < 0.
Áp dụng công thức tanα.cotα = 1, ta có \(\cot \alpha = \frac{1}{{\tan \alpha }} = \frac{1}{3}\).
Áp dụng công thức \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\), ta có:
\(1 + {3^2} = \frac{1}{{{{\cos }^2}\alpha }}\) hay \(\frac{1}{{{{\cos }^2}\alpha }} = 10\)
\( \Rightarrow {\cos ^2}\alpha = \frac{1}{{10}} \Rightarrow \cos \alpha = - \frac{{\sqrt {10} }}{{10}}\) (do cosα < 0).
Áp dụng công thức \(1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\), ta có:
\(1 + {\left( {\frac{1}{3}} \right)^2} = \frac{1}{{{{\sin }^2}\alpha }}\) hay \(\frac{1}{{{{\sin }^2}\alpha }} = \frac{{10}}{9}\)
\( \Rightarrow {\sin ^2}\alpha = \frac{9}{{10}} \Rightarrow \sin \alpha = - \frac{3}{{\sqrt {10} }} = - \frac{{3\sqrt {10} }}{{10}}\) (do sinα < 0).
Vậy \(\sin \alpha = \frac{{3\sqrt {10} }}{{10}}\); \(\cos \alpha = - \frac{{\sqrt {10} }}{{10}}\); \(\cot \alpha = \frac{1}{3}\).
Câu 40:
Tính các giá trị lượng giác của góc alpha trong trường hợp sau:
cotα = ‒2 với 0 < α < π
 Xem đáp án
Xem đáp án
cotα = ‒2 với 0 < α < π.
Áp dụng công thức tanα.cotα = 1, ta có \(\tan \alpha = \frac{1}{{\cot \alpha }} = \frac{1}{{ - 2}} = - \frac{1}{2}\).
Do 0 < α < π nên sinα > 0.
Mà cotα = ‒2 < 0 nên \(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} < 0\), suy ra cosα < 0.
Áp dụng công thức \(1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\), ta có:
\(1 + {\left( { - 2} \right)^2} = \frac{1}{{{{\sin }^2}\alpha }}\) hay \(\frac{1}{{{{\sin }^2}\alpha }} = 5\)
\( \Rightarrow {\sin ^2}\alpha = \frac{1}{5} \Rightarrow \sin \alpha = \frac{1}{{\sqrt 5 }} = \frac{{\sqrt 5 }}{5}\) (do sinα > 0).
Ta có: \(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} \Rightarrow \cos \alpha = \cot \alpha .\sin \alpha = \left( { - 2} \right).\frac{{\sqrt 5 }}{5} = - \frac{{2\sqrt 5 }}{5}\).
Câu 41:
Một vệ tinh được định vị tại vị trí A trong không gian. Từ vị trí A, vệ tinh bắt đầu chuyển động quanh Trái Đất theo quỹ đạo là đường tròn với tâm là tâm O của Trái Đất, bán kính 9 000 km. Biết rằng vệ tinh chuyển động hết một vòng của quỹ đạo trong 2 h.
 Xem đáp án
Xem đáp án
Giả sử vệ tinh được định tại vị trí A, chuyển động quanh Trái Đất được mô tả như hình vẽ dưới đây:
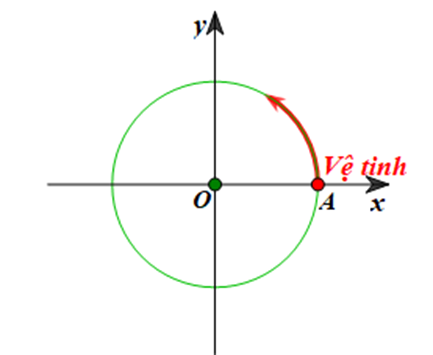
Vệ tinh chuyển động hết một vòng của quỹ đạo tức là vệ tinh chuyển động được quãng đường bằng chu vi của quỹ đạo là đường tròn với tâm là tâm O của Trái Đất, bán kính 9 000 km.
Do đó quãng đường vệ tinh đã chuyển động được sau 2 h là:
2π . 9 000 = 18 000π (km).
Quãng đường vệ tinh đã chuyển động được sau 1 h là: \[\frac{{18\,000\pi }}{2}.1 = 9000\pi \,\,\,\left( {km} \right)\].
Quãng đường vệ tinh đã chuyển động được sau 3 h là: \[\frac{{18000\pi }}{2}.3 = 27000\pi \,\,\,\left( {km} \right)\].
Quãng đường vệ tinh đã chuyển động được sau 5 h là: \[\frac{{18000\pi }}{2}.5 = 45000\pi \,\,\,\left( {km} \right)\].
Câu 42:
Một vệ tinh được định vị tại vị trí A trong không gian. Từ vị trí A, vệ tinh bắt đầu chuyển động quanh Trái Đất theo quỹ đạo là đường tròn với tâm là tâm O của Trái Đất, bán kính 9 000 km. Biết rằng vệ tinh chuyển động hết một vòng của quỹ đạo trong 2 h.
Vệ tinh chuyển động được quãng đường 200 000 km sau bao nhiêu giờ (làm tròn kết quả đến hàng đơn vị)?
 Xem đáp án
Xem đáp án
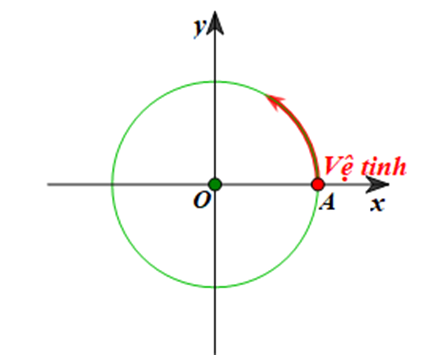
Ta thấy vệ tinh chuyển động được quãng đường là 9000π (km) trong 1h.
Vậy vệ tinh chuyển động được quãng đường 200 000 km trong thời gian là:
\(\frac{{200\,\,000}}{{9000\pi }} \approx 7\) (giờ).
