Thi Online (2023) Đề thi thử Vật Lí THPT Nguyễn Khuyến Lần 2 có đáp án
Thi Online (2023) Đề thi thử Vật Lí THPT Nguyễn Khuyến Lần 2 có đáp án
-
642 lượt thi
-
40 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Trong hiện tượng giao thoa sóng cơ với hai nguồn kết hợp \({\rm{A}}\) và \({\rm{B}}\) có bước sóng \(\lambda \) thì khoảng cách giữa hai điểm gần nhau nhất trên đoạn \({\rm{AB}}\) dao động với biên độ cực đại là
 Xem đáp án
Xem đáp án
Chọn A.
Câu 5:
Trong dao động cưỡng bức, khi xảy ra hiện tượng cộng hưởng thì đại lượng nào sau đây tăng đến giá trị cực đại?
 Xem đáp án
Xem đáp án
Câu 6:
Biết cường độ âm chuẩn là \({{\rm{I}}_0}\). Tại một điểm trong môi trường truyền âm có mức cường độ âm là \({\rm{I}}\) thì mức cường độ âm là
 Xem đáp án
Xem đáp án
Chọn C.
Câu 7:
Để có sóng dừng trên một sợi dây đàn hồi với hai đầu cố định thì chiều dài dây bằng
 Xem đáp án
Xem đáp án
Chọn B.
Câu 8:
Gọi \(\omega ,{\rm{T}},{\rm{f}}\) lần lượt là tần số góc, chu kì và tần số của một vật dao động điều hòa. Hệ thức đúng là
 Xem đáp án
Xem đáp án
Câu 10:
Độ lệch pha của hai dao động điều hòa cùng phương, cùng tần số và ngược pha nhau là
 Xem đáp án
Xem đáp án
Chọn C.
Câu 11:
 Xem đáp án
Xem đáp án
Chọn A.
Câu 12:
Đối với sóng dừng trên một sợi dây đàn hồi, khoảng cách nhỏ nhất giữa một bụng sóng và một nút sóng bằng
 Xem đáp án
Xem đáp án
Câu 13:
Trong sóng cơ, công thức liên hệ giữa tốc độ truyền sóng v, bước sóng \(\lambda \), chu kì \(T\) của sóng là
 Xem đáp án
Xem đáp án
Chọn D.
Câu 14:
Một con lắc đơn có độ dài dây treo bằng \(\ell \), treo tại nơi có gia tốc trọng trường g. Khi con lắc đơn dao động điều hòa thì biểu thức tần số là
 Xem đáp án
Xem đáp án
Chọn D.
Câu 15:
Trong hiện tượng giao thoa sóng ở mặt nước với hai nguồn sóng kết hợp dao động điều hòa cùng pha. Sóng truyền ở mặt nước có bước sóng \(\lambda \). Cực tiểu giao thoa nằm tại những điểm có hiệu đường đi của hai sóng từ hai nguồn tới điểm đó bằng
 Xem đáp án
Xem đáp án
Câu 16:
Tại một nơi trên mặt đất có \({\rm{g}} = 9,8{\rm{\;m}}/{{\rm{s}}^2}\), một con lắc đơn dao động điều hòa với chu kì 0,9 s, chiều dài của con lắc xấp xỉ là
 Xem đáp án
Xem đáp án
Chọn B.
Câu 17:
Một chất điểm dao động điều hòa trên trục \({\rm{Ox}}\) theo phương trình \({\rm{x}} = 4{\rm{cos}}\left( {2{\rm{t}}} \right)\left( {{\rm{cm}}} \right)\). Quãng đường chất điểm đi được trong 2 chu kì dao động là
 Xem đáp án
Xem đáp án
Chọn D.
\(t = 2T \Rightarrow s = 2.4A = 8A = 8.4 = 32\;cm.\)
Câu 18:
Một vật dao động diều hòa trên quỹ đạo có chiều dài \(10{\rm{\;cm}}\). Biên độ dao động của vật bằng
 Xem đáp án
Xem đáp án
Chọn C.
\(L = 2A \Rightarrow A = \frac{L}{2} = \frac{{10}}{2} = 5\).
Câu 19:
Hai con lắc đơn dao động điều hoà tại cùng một nơi với chu kì dao động lần lượt là \(1,8{\rm{\;s}}\) và \(1,5{\rm{\;s}}\). Tỉ số chiều dài của con lắc thứ nhất và con lắc thứ hai là
 Xem đáp án
Xem đáp án
Chọn C.
\(T\~\sqrt l \Rightarrow \frac{{{T_1}}}{{{T_2}}} = \sqrt {\frac{{{l_1}}}{{{l_2}}}} \Rightarrow \frac{{{l_1}}}{{{l_2}}} = \frac{{T_1^2}}{{T_2^2}} = \frac{{1,{8^2}}}{{1,{5^2}}} = 1,44\).
Câu 20:
Một con lắc đơn gồm dây treo dài \(50{\rm{\;cm}}\) và vật nhỏ có khối lượng \(100{\rm{\;g}}\) dao động điều hòa với biên độ góc \({5^ \circ }\), tại nơi có gia tốc trọng trường \({\rm{g}} = 10{\rm{\;m}}/{{\rm{s}}^2}\). Lấy \(\pi = 3,14\). Cơ năng của con lắc có giá trị bằng
 Xem đáp án
Xem đáp án
Chọn B.
\(W = {\left( {{W_t}} \right)_{max}} = mgl\left( {1 - \cos \alpha } \right) = 0,1.10.0,5.\left( {1 - \cos 5} \right) = 1,{9.10^{ - 3}}J = 1,9mJ.\)
Câu 21:
Một sóng cơ học tần số \(25{\rm{\;Hz}}\) truyền dọc theo trục \({\rm{Ox}}\) với tốc độ \(100{\rm{\;cm}}/{\rm{s}}\). Hai điểm gần nhau nhất trên trục \({\rm{Ox}}\) mà các phần tử sóng tại đó dao động ngược pha cách nhau
 Xem đáp án
Xem đáp án
Chọn D.
\(\frac{\lambda }{2} = \frac{v}{{2f}} = \frac{{100}}{{2.25}} = 2cm\).
Câu 22:
Phương trình sóng tại nguồn \({\rm{O}}\) có dạng \({\rm{u}} = 4{\rm{cos}}\left( {\frac{\pi }{3}{\rm{t}}} \right)\) ( \(u\) tính bằng \({\rm{cm}}\), t tính bằng \({\rm{s}}\) ). Bước sóng \(\lambda = 240{\rm{\;cm}}\). Tốc độ truyền sóng bằng
 Xem đáp án
Xem đáp án
Chọn A.
\(v = \lambda .\frac{\omega }{{2\pi }} = 240.\frac{{\frac{\pi }{3}}}{{2\pi }} = 40\;\left( {cm/s} \right).\)
Câu 23:
 Xem đáp án
Xem đáp án
Chọn D.
\(A = \frac{L}{2} = \frac{{20}}{2} = 10\;cm = 0,1\;m.\)
\(W = \frac{1}{2}k{A^2} = \frac{1}{2}.20.0,{1^2} = 0,1J\)
Câu 24:
 Xem đáp án
Xem đáp án
Chọn C.
Quãng đường đi được trong 1 chu kì: \(s = 4A\).
Vận tốc trung bình: \({v_{tb}} = \frac{s}{t} = \frac{{4A}}{T} = \frac{{4\omega A}}{{2\pi }} = \frac{{4.{v_{max}}}}{{2\pi }} = 20 \Rightarrow {v_{max}} = \frac{{20.2\pi }}{4} = 10\pi \)
Câu 25:
Trên một sợi dây đàn hồi dài \(1,2{\rm{\;m}}\), hai đầu cố định, đang có sóng dừng. Biết sóng truyền trên dây có tần số \(100{\rm{\;Hz}}\) và tốc độ \(80{\rm{\;m}}/{\rm{s}}\). Số bụng sóng trên dây là
 Xem đáp án
Xem đáp án
Chọn B.
\(\lambda = \frac{v}{f} = \frac{{80}}{{100}} = 0,8m;l = k.\frac{\lambda }{2} \Leftrightarrow 1,2 = k.\frac{{0,8}}{2} \Rightarrow k = 3.\)
Câu 26:
Hai dao động điều hòa cùng phương, cùng tần số, có biên độ lần lượt là \({{\rm{A}}_1} = \) \(4,5{\rm{\;cm}};{A_2} = 6{\rm{\;cm}}\); lệch pha nhau \(\pi \). Dao động tổng hợp của hai dao động này có biên độ bằng
 Xem đáp án
Xem đáp án
Chọn A.
\(A = \left| {{A_1} - {A_2}} \right| = \left| {4,5 - 6} \right| = 1,5\;cm.\)
Câu 27:
Biết cường độ âm chuẩn là \({10^{ - 12}}{\rm{\;W}}/{{\rm{m}}^2}\). Tại điểm có cường độ âm là \({10^{ - 4}}{\rm{\;W}}/{{\rm{m}}^2}\) thì mức cường độ âm bằng
 Xem đáp án
Xem đáp án
Câu 28:
Một con lắc lò xo gồm lò xo có độ cứng \({\rm{k}} = 40{\rm{\;N}}/{\rm{m}}\), quả cầu nhỏ có khối lượng \({\rm{m}}\) đang dao động tự do với chu kì \({\rm{T}} = 0,1\pi {\rm{s}}\). Khối lượng của quả cầu là
 Xem đáp án
Xem đáp án
Chọn A.
\({\rm{\lambda }} = \frac{{\rm{v}}}{{\rm{f}}} = \frac{{20}}{{40}} = 0,5{\rm{m}} = 50{\rm{cm}}.\)\({\rm{l}} = {\rm{k}}.\frac{{\rm{\lambda }}}{2} \Rightarrow 100 = {\rm{k}}.\frac{{50}}{2} \Rightarrow {\rm{k}} = 4.{\rm{\;}}\)cứ 1 bó có 2 vị trí biên độ 2 cm nên có 8 điểm.
Câu 29:
Một sợi dây \(AB\) dài \(100{\rm{\;cm}}\) căng ngang với hai đầu cố định đang có sóng dừng. Sóng truyền trên dây với tần số \(40{\rm{\;Hz}}\) và tốc độ \(20{\rm{\;m}}/{\rm{s}}\). Biết biên độ dao động của điểm bụng là \(4{\rm{\;cm}}\). Trên dây, số điểm dao động với biên độ \(2{\rm{\;cm}}\) là
 Xem đáp án
Xem đáp án
Chọn A.
\({\rm{\lambda }} = \frac{{\rm{v}}}{{\rm{f}}} = \frac{{20}}{{40}} = 0,5{\rm{m}} = 50{\rm{cm}}.\)\({\rm{l}} = {\rm{k}}.\frac{{\rm{\lambda }}}{2} \Rightarrow 100 = {\rm{k}}.\frac{{50}}{2} \Rightarrow {\rm{k}} = 4.{\rm{\;}}\)cứ 1 bó có 2 vị trí biên độ 2 cm nên có 8 điểm.
Câu 30:
Một sóng âm truyền trong không khí. Mức cường độ âm tại điểm \(M\) và tại điểm \({\rm{N}}\) lần lượt là \(40{\rm{\;dB}}\) và \(80\) d Cường độ âm tại \({\rm{N}}\) lớn hơn cường độ âm tại \({\rm{M}}\)
 Xem đáp án
Xem đáp án
Chọn B.
\({L_N} - {L_M} = 10.\log \frac{{{I_N}}}{{{I_M}}} \Rightarrow \frac{{{I_N}}}{{{I_M}}} = {10^{{L_N} - {L_M}}} = {10^{8 - 4}} = {10^4}.\)
Câu 31:
Ở mặt chất lỏng có hai nguồn sóng A, B cách nhau \(20{\rm{\;cm}}\), dao động theo phương thẳng đứng với phương trình là \({{\rm{u}}_{\rm{A}}} = {{\rm{u}}_{\rm{B}}} = 2{\rm{cos}}50\pi {\rm{t}}\) (\({\rm{t}}\) tính bằng \({\rm{s}}\)). Tốc độ truyền sóng trên mặt chất lỏng là \(1,5{\rm{\;m}}/{\rm{s}}\). Trên đoạn thẳng \({\rm{AB}}\), số điểm có biên độ dao động cực đại và số điểm đứng yên lần lượt là
 Xem đáp án
Xem đáp án
Chọn C.
\(\lambda = v.T = v.\frac{{2\pi }}{\omega } = \frac{{1,5.2\pi }}{{50\pi }} = 0,06m = 6cm.\)\( - \frac{{AB}}{\lambda } < k < \frac{{AB}}{\lambda } \Rightarrow - \frac{{20}}{3} < k < \frac{{20}}{3} \Rightarrow - 3,3 < k < 3,3.\)
Có 7 giá trị k nguyên và 6 giá trị bán nguyên è Có 7 cực đại và 6 cực tiểu.
Câu 32:
Ở mặt chất lỏng, tại hai điểm \({{\rm{S}}_1}\) và \({{\rm{S}}_2}\) có hai nguồn dao động cùng pha theo phương thẳng đứng phát ra hai sóng kết hợp có bước sóng \(1{\rm{\;cm}}\). Trong vùng giao thoa, \(M\) là điểm cách \({{\rm{S}}_1}\) và \({{\rm{S}}_2}\) lần lượt là \(7{\rm{\;cm}}\) và \(12{\rm{\;cm}}\). Giữa \({\rm{M}}\) và đường trung trực của đoạn thẳng \({{\rm{S}}_1}{\rm{\;}}{{\rm{S}}_2}\) có số vân giao thoa cực tiểu là
 Xem đáp án
Xem đáp án
Chọn A.
\(0 < {\rm{k}} < \frac{{\left( {{\rm{M}}{{\rm{S}}_2} - {\rm{M}}{{\rm{S}}_1}} \right)}}{{\rm{\lambda }}} \Rightarrow 0 < {\rm{k}} < \frac{{12 - 7}}{1} \Rightarrow 0 < {\rm{k}} < 5.\) có 5 giá trị bán nguyên
Câu 33:
Dao động của một vật là tổng hợp của hai dao động cùng phương có phương trình lần lượt là \({{\rm{x}}_1} = 3{\rm{cos}}4\pi {\rm{t}}\left( {{\rm{cm}}} \right)\) và \({{\rm{x}}_2} = 4{\rm{cos}}\left( {4\pi {\rm{t}} + \varphi } \right)\left( {{\rm{cm}}} \right)({\rm{t}}\) tính bằng \({\rm{s}})\). Tại \({\rm{t}} = 0,25{\rm{\;s}}\), vật có li độ lớn nhất. Biên độ dao động của vật là
 Xem đáp án
Xem đáp án
Chọn C.
Tại t = 0,25s thì x = A ở biên dương và \({x_1} = 3\cos \left( {4\pi .0,25} \right) = - 3cm\) ở biên âm. ở biên âm.
è x và x1 ngược pha è x2 và x1 ngược pha è A = |A2 – A1| = 4 – 3 = 1 cm.
Câu 34:
Một con lắc lò xo gồm vật nhỏ có khối lượng \({\rm{m}} = 100{\rm{\;g}}\), lò xo có độ cứng \({\rm{k}}\) được treo thẳng đứng. Kích thích cho vật dao động điều hòa với biên độ \({\rm{A}}\). Chọn gốc thế năng tại vị trí cân bằng của vật. Hình bên là một phần đồ thị biểu diễn mối liên hệ giữa thế năng \({{\rm{E}}_{\rm{t}}}\) và độ lớn lực kéo về \(\left| {{{\rm{F}}_{{\rm{kv}}}}} \right|\) khi vật dao động. Chu kì dao động của vật là
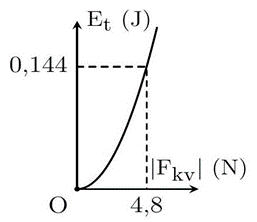
 Xem đáp án
Xem đáp án
Chọn A.
\(\left\{ {\begin{array}{*{20}{c}}{{E_t} = \frac{1}{k}.{x^2}}\\{\left| {{F_{kv}}} \right| = k\left| x \right|}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{c}}{0,144 = \frac{1}{2}k.{x^2}}\\{4,8 = k\left| x \right|}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{c}}{\left| x \right| = 0,06m}\\{k = \frac{{80N}}{m}}\end{array}} \right.} \right.} \right.\)\(T = 2\pi \sqrt {\frac{m}{k}} = 2\pi \sqrt {\frac{{0,1}}{{80}}} \approx 0,222s\;\)
Câu 35:
Một con lắc lò xo treo thẳng đứng, vật nặng có khối lượng \(1,5{\rm{\;kg}}\). Kích thích cho con lắc dao động điều hòa quanh vị trí cân bằng. Biểu thức lực kéo về tác dụng lên vật là \({\rm{F}} = 6{\rm{cos}}\left( {10{\rm{t}} + \frac{\pi }{6}} \right){\rm{\;}}\left( {\rm{N}} \right)\). Cho \({\rm{g}} = 10{\rm{\;m}}/{{\rm{s}}^2}\). Lực đàn hồi cực đại tác dụng lên con lắc bằng
 Xem đáp án
Xem đáp án
Câu 36:
Trên mặt nước cho hai nguồn kết hợp dao động cùng phương, cùng pha đặt tại hai điểm A, B. Sóng do hai nguồn tạo ra có bước sóng \(\lambda = 2{\rm{\;cm}}\). Gọi \(\left( {\rm{C}} \right)\) là đường tròn đường kính \({\rm{AB}}.\) Biết rằng trên \(\left( {\rm{C}} \right)\) có 30 điểm dao động với biên độ cực đại, trong đó có 6 điểm dao động với biên độ cực đại cùng pha với nguồn. Độ dài đoạn \({\rm{AB}}\) gần nhất với giá trị nào sau đây?
 Xem đáp án
Xem đáp án
Chọn C.
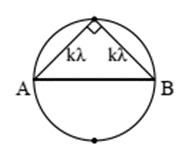
Trên (C) có 30 điểm thì trừ 2 điểm ở trung trực thì mỗi bên có 14 điểm ứng với 7 đường cục đại: \(7 < \frac{{AB}}{\lambda } < 8\)
Trên (C) có 6 điểm cùng pha nguồn nên trong đó phải có 2 điểm ở trung trực.
\( \Rightarrow k\lambda = \frac{{AB}}{{\sqrt 2 }} \Rightarrow k = \frac{{AB}}{{\lambda \sqrt 2 }}\mathop \to \limits^{7 < \frac{{AB}}{\lambda } < 8} 4,95 < k < 5,65 \Rightarrow k = 5 \to AB = 5\lambda \sqrt 2 = 10\sqrt 2 \;cm\)
Câu 37:
Một sóng cơ lan truyền trên sợi dây từ \({\rm{B}}\) đến \({\rm{C}}\) với chu kì \({\rm{T}} = 2{\rm{\;s}}\), biên độ không đổi. Ở thời điểm \({{\rm{t}}_0}\), li độ các phần tử tại \({\rm{B}}\) và \({\rm{C}}\) tương ứng là \( - 20{\rm{\;mm}}\) và \( + 20{\rm{\;mm}}\); phần tử tại trung điểm \({\rm{D}}\) của \({\rm{BC}}\) đang ở vị trí cân bằng. Ở thời điểm \({{\rm{t}}_1}\), li độ các phần tử tại \({\rm{B}}\) và \({\rm{C}}\) cùng là \( + 15{\rm{\;mm}}\). Tại thời điểm \({{\rm{t}}_2} = {{\rm{t}}_1} + 0,25{\rm{\;s}}\) li độ của phần tử \({\rm{D}}\) có độ lớn gần nhất với giá trị nào sau đây?
 Xem đáp án
Xem đáp án
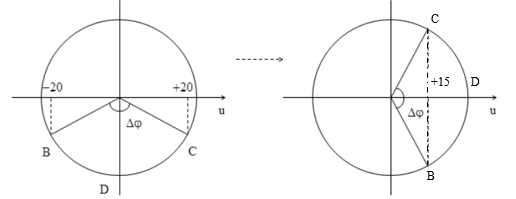
Chọn D.
Theo giả thiết, vị trí của B, D, C phải thoả mãn như hình vẽ.
Hình 1: \(\sin \frac{{\Delta {\rm{\varphi }}}}{2} = \frac{{20}}{{\rm{A}}}\); Hình 2: \(\cos \frac{{\Delta {\rm{\varphi }}}}{2} = \frac{{15}}{{\rm{A}}}\)
\({\rm{m\`a \;}}{\sin ^2}\frac{{\Delta {\rm{\varphi }}}}{2} + {\cos ^2}\frac{{\Delta {\rm{\varphi }}}}{2} = 1{\rm{\;n\^e n\;A}} = \sqrt {{{20}^2} + {{15}^2}} = 25{\rm{mm}}.\)
\(\Delta t = 0,25 = \frac{T}{8} \Rightarrow {x_D} = \frac{{A\sqrt 2 }}{2} = \frac{{25\sqrt 2 }}{2} \approx 17,7mm.\)
Câu 38:
Cho hệ con lắc lò xo được bố trí như hình vẽ, lò xo có độ cứng \({\rm{k}} = 24{\rm{\;N}}/{\rm{m}}\), vật nặng có khối lượng \({\rm{m}} = 100{\rm{\;g}}\), lấy \({\rm{g}} = 10{\rm{\;m}}/{{\rm{s}}^2}\). Gọi \({\rm{O}}\) là vị trí của vật khi lò xo không biến dạng. Vật có thể chuyển động không ma sát trên đoạn x'O nhưng đoạn Ox vật chịu tác dụng của lực ma sát có hệ số ma sát \(\mu = 0,25\). Ban đầu vật được giữ tại vị trí mà lò xo bị nén \(13{\rm{\;cm}}\) rồi thả nhẹ để vật dao động. Sau khi vật đổi chiều chuyển động, lò xo bị nén nhiều nhất một đoạn có giá trị xấp xỉ là
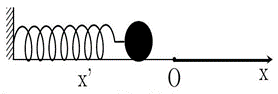
 Xem đáp án
Xem đáp án
Chọn B.
\({F_{ms}} = \mu mg = 0,25.0,1.10 = 0,25\;\left( N \right)\)
Quá trình 1: x’ à O à x
Cơ năng tại O: \({W_O} = \frac{1}{2}.k{A^2}\); Cơ năng tại biên A’: \({W_{A'}} = \frac{1}{2}k{A^{'2}}\)
Định lý cơ năng: \({W_O} - {W_{A'}} = {A_{{F_{ms}}}}\; \Rightarrow \frac{1}{2}.24.0,{13^2} - \frac{1}{2}.24.{A^{'2}} = 0,25.A' \Rightarrow A' = 0,12m.\)
Quá trình 2: x à O
Cơ năng tại O (lúc này biên độ là A”): \({W_O} = \frac{1}{2}.kA'{'^2}\); Cơ năng tại biên A’: \({W_{A'}} = \frac{1}{2}k{A^{'2}}\)
Định lý cơ năng: \({W_{A'}} - {W_O} = {A_{{F_{ms}}}}\; \Rightarrow \frac{1}{2}.24.0,{12^2} - \frac{1}{2}.24.A'{'^2} = 0,25.0,12\)
\( \Rightarrow A'' = 0,109m = 10,9cm.\)
Quá trình 3: O à x’. Lò xo nén lớn nhất bằng A” = 10,9 cm.
Câu 39:
Trên một sợi dây đàn hồi đang có sóng dừng ổn định với khoảng cách giữa hai vị trí cân bằng của một bụng sóng với một nút sóng cạnh nhau là \(6{\rm{\;cm}}\). Tốc độ truyền sóng trên dây là \(1,2{\rm{\;m}}/{\rm{s}}\) và biên độ dao động của bụng sóng là \(4{\rm{\;cm}}\). Gọi \({\rm{N}}\) là vị trí nút sóng, \({\rm{P}}\) và \({\rm{Q}}\) là hai phần tử trên dây và ở hai bên của \({\rm{N}}\) có vị trí cân bằng cách \({\rm{N}}\) lần lượt là 15 \({\rm{cm}}\) và \(16{\rm{\;cm}}\). Tại thời điểm \({\rm{t}}\), phần tử \({\rm{P}}\) có li độ \(\sqrt 2 {\rm{\;cm}}\) và đang hướng về vị trí cân bằng. Sau thời điểm đó một khoảng thời gian \({\rm{\Delta t}}\) thì phần tử \({\rm{Q}}\) có li độ là \(3{\rm{\;cm}}\), giá trị của \({\rm{\Delta t}}\) là
 Xem đáp án
Xem đáp án
Chọn D.
\(\frac{{\rm{\lambda }}}{4} = 6{\rm{cm\;}} \Rightarrow {\rm{\lambda }} = 24{\rm{cm\;v\`a \;\omega }} = 2{\rm{\pi }}.\frac{{\rm{v}}}{{\rm{\lambda }}} = 2{\rm{\pi }}.\frac{{120}}{{24}} = 10{\rm{\pi \;}}\left( {{\rm{rad}}/{\rm{s}}} \right)\)
\(A = 4\left| {\sin \left( {\frac{{2\pi d}}{\lambda }} \right)} \right| \Rightarrow \left\{ {\begin{array}{*{20}{c}}{{A_P} = 4\left| {\sin \left( {\frac{{2\pi .15}}{{24}}} \right)} \right| = 2\sqrt 2 cm}\\{{A_Q} = 4\left| {\sin \left( {\frac{{2\pi .16}}{{24}}} \right)} \right| = 2\sqrt 3 cm}\end{array}} \right.\)
P ngược pha Q\( \Rightarrow \frac{{{{\rm{u}}_{\rm{Q}}}}}{{{{\rm{A}}_{\rm{Q}}}}} = - \frac{{{{\rm{u}}_{\rm{P}}}}}{{{{\rm{A}}_{\rm{P}}}}} = - \frac{{\sqrt 2 }}{{2\sqrt 2 }} = - \frac{1}{2}\) và đang hướng về VTCB \( \Rightarrow {{\rm{\varphi }}_{\rm{Q}}} = - \frac{{2{\rm{\pi }}}}{3}\)
\( \Rightarrow {{\rm{u}}_{\rm{Q}}} = 2\sqrt 3 \cos \left( {10{\rm{\pi t}} - \frac{{2{\rm{\pi }}}}{3}} \right)\mathop \to \limits^{{{\rm{u}}_{\rm{Q}}} = 3} \Delta {\rm{t}} = 0,05{\rm{s}}\)
Câu 40:
Một con lắc đơn gồm dây treo có chiều dài \(\ell = 120{\rm{\;cm}}\) chịu được lực căng tối đa \(2,5{\rm{\;N}}\) và vật nặng có khối lượng \({\rm{m}} = 100{\rm{\;g}}\) được treo vào điểm \({\rm{T}}\) cố định. Biết phía dưới điểm \({\rm{T}}\) theo phương thẳng đứng có một đinh I cố định. Ban đầu con lắc được kéo ra khỏi vị trí cân bằng để cho dây treo hợp với phương thẳng đứng một góc \({\alpha _0} = {60^ \circ }\) rồi thả nhẹ, lấy \({\rm{g}} = 10{\rm{\;m}}/{{\rm{s}}^2}\). Khoảng cách lớn nhất giữa đinh và điểm treo để dây không bị đứt khi con lắc dao động là
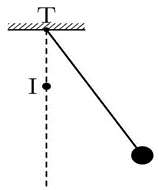
 Xem đáp án
Xem đáp án
Chọn C.
Từ biên đến VTCB, lực căng dây tại VTCB cực đại (với a’0 sau khi vướng đinh).
\({T_{max}} = mg\left( {3 - 2\cos \alpha _0^'} \right) \Rightarrow 2,5 = 0,1.10\left( {3 - 2\cos \alpha _0^'} \right) \to \cos \alpha _0^' = 0,25.\)
Tại VTCB, vận tốc khi chưa vướng đinh = vận tốc khi vướng đinh.
\(v_{max}^2 = 2gl.\left( {1 - \cos {\alpha _0}} \right) = 2gl'\left( {1 - \cos \alpha _0^'} \right) \Rightarrow 120.\left( {1 - \cos 60} \right) = l'.\left( {1 - 0,25} \right) \Rightarrow l' = 80cm.\)
\(l - l' = 120 - 80 = 40\;cm.\)
