Giải SBT Toán 11 Cánh Diều Các phép biến đổi lượng giác có đáp án
-
253 lượt thi
-
10 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho \(\sin a = \frac{2}{3}\) với \(\frac{\pi }{2} < a < \pi \). Tính:
cos a, tan a;
 Xem đáp án
Xem đáp án
Vì \(\frac{\pi }{2} < a < \pi \) nên cos a < 0, do đó từ sin2 a + cos2 a = 1, suy ra
\(\cos a = - \sqrt {1 - {{\sin }^2}a} = - \sqrt {1 - {{\left( {\frac{2}{3}} \right)}^2}} = - \frac{{\sqrt 5 }}{3}\).
Ta có \(\tan a = \frac{{\sin a}}{{\cos a}} = \frac{{\frac{2}{3}}}{{ - \frac{{\sqrt 5 }}{3}}} = - \frac{{2\sqrt 5 }}{5}\).
Câu 2:
Cho \(\sin a = \frac{2}{3}\) với \(\frac{\pi }{2} < a < \pi \). Tính:
\(\sin \left( {a + \frac{\pi }{4}} \right),\,\cos \left( {a - \frac{{5\pi }}{6}} \right),\,\tan \left( {a + \frac{{2\pi }}{3}} \right)\);
 Xem đáp án
Xem đáp án
\(\sin \left( {a + \frac{\pi }{4}} \right)\)\( = \sin a\cos \frac{\pi }{4} + \cos a\sin \frac{\pi }{4}\)\( = \frac{2}{3}.\frac{{\sqrt 2 }}{2} + \left( { - \frac{{\sqrt 5 }}{3}} \right).\frac{{\sqrt 2 }}{2} = \frac{{2\sqrt 2 - \sqrt {10} }}{6}\).
\(\cos \left( {a - \frac{{5\pi }}{6}} \right)\)\( = \cos a\cos \frac{{5\pi }}{6} + \sin a\sin \frac{{5\pi }}{6}\)\( = \left( { - \frac{{\sqrt 5 }}{3}} \right).\left( { - \frac{{\sqrt 3 }}{2}} \right) + \frac{2}{3}.\frac{1}{2} = \frac{{\sqrt {15} + 2}}{6}\).
\(\tan \left( {a + \frac{{2\pi }}{3}} \right)\)\( = \frac{{\tan a + \tan \frac{{2\pi }}{3}}}{{1 - \tan a\tan \frac{{2\pi }}{3}}} = \frac{{ - \frac{{2\sqrt 5 }}{5} + \left( { - \sqrt 3 } \right)}}{{1 - \left( { - \frac{{2\sqrt 5 }}{5}} \right).\left( { - \sqrt 3 } \right)}} = \frac{{8\sqrt 5 + 9\sqrt 3 }}{7}\).
Câu 3:
Cho \(\sin a = \frac{2}{3}\) với \(\frac{\pi }{2} < a < \pi \). Tính:
sin 2a, cos 2a.
 Xem đáp án
Xem đáp án
\(\sin 2a = 2\sin a\cos a = 2.\frac{2}{3}.\left( { - \frac{{\sqrt 5 }}{3}} \right) = - \frac{{4\sqrt 5 }}{9}\).
\(\cos 2a = 2{\cos ^2}a - 1 = 2.{\left( { - \frac{{\sqrt 5 }}{3}} \right)^2} - 1 = \frac{1}{9}\).Câu 4:
Cho cos a = 0,2 với π < a < 2π. Tính \(\sin \frac{a}{2}\), \(\cos \frac{a}{2}\), \(\tan \frac{a}{2}\).
 Xem đáp án
Xem đáp án
Do π < a < 2π nên \(\frac{\pi }{2} < \frac{a}{2} < \pi \). Suy ra \(\sin \frac{a}{2} > 0,\,\,\cos \frac{a}{2} < 0\).
Ta có: \({\sin ^2}\frac{a}{2} = \frac{{1 - \cos a}}{2} = \frac{{1 - 0,2}}{2} = 0,4\), suy ra \(\sin \frac{a}{2} = \frac{{\sqrt {10} }}{5}\).
Do đó, \(\cos \frac{a}{2} = - \sqrt {1 - {{\sin }^2}\frac{a}{2}} = - \sqrt {1 - {{\left( {\frac{{\sqrt {10} }}{5}} \right)}^2}} = - \frac{{\sqrt {15} }}{5}\).
\(\tan \frac{a}{2} = \frac{{\sin \frac{a}{2}}}{{\cos \frac{a}{2}}} = \frac{{\frac{{\sqrt {10} }}{5}}}{{ - \frac{{\sqrt {15} }}{5}}} = - \frac{{\sqrt 6 }}{3}\).
Câu 5:
Cho \(\tan \frac{a}{2} = \frac{1}{{\sqrt 2 }}\). Tính sin a, cos a, tan a.
 Xem đáp án
Xem đáp án
Ta có \(\sin a = 2\sin \frac{a}{2}\cos \frac{a}{2} = \frac{{2\sin \frac{a}{2}\cos \frac{a}{2}}}{{{{\sin }^2}\frac{a}{2} + {{\cos }^2}\frac{a}{2}}}\) (do \({\sin ^2}\frac{a}{2} + {\cos ^2}\frac{a}{2} = 1\))
\( = \frac{{2\tan \frac{a}{2}}}{{{{\tan }^2}\frac{a}{2} + 1}} = \frac{{2.\frac{1}{{\sqrt 2 }}}}{{{{\left( {\frac{1}{{\sqrt 2 }}} \right)}^2} + 1}} = \frac{{2\sqrt 2 }}{3}\).
\(\cos a = {\cos ^2}\frac{a}{2} - {\sin ^2}\frac{a}{2} = \frac{{{{\cos }^2}\frac{a}{2} - {{\sin }^2}\frac{a}{2}}}{{{{\sin }^2}\frac{a}{2} + {{\cos }^2}\frac{a}{2}}}\)\( = \frac{{1 - {{\tan }^2}\frac{a}{2}}}{{{{\tan }^2}\frac{a}{2} + 1}} = \frac{{1 - {{\left( {\frac{1}{{\sqrt 2 }}} \right)}^2}}}{{{{\left( {\frac{1}{{\sqrt 2 }}} \right)}^2} + 1}} = \frac{1}{3}\).
\(\tan a = \frac{{\sin a}}{{\cos a}} = \frac{{\frac{{2\sqrt 2 }}{3}}}{{\frac{1}{3}}} = 2\sqrt 2 \).
Câu 6:
Cho cos(a + 2b) = 2cos a. Chứng minh rằng: tan(a + b) tan b = \(\frac{{ - 1}}{3}\).
 Xem đáp án
Xem đáp án
Ta có cos(a + 2b) = 2cos a
⇔ cos[(a + b) + b] = 2cos[(a + b) – b]
⇔ cos(a + b) . cos b – sin(a + b) . sin b = 2[cos(a + b) . cos b + sin(a + b) . sin b]
⇔ cos(a + b) . cos b – 2 cos(a + b) . cos b = 2 sin(a + b) . sin b + sin(a + b) . sin b
⇔ – cos(a + b) . cos b = 3 sin(a + b) . sin b
⇔ sin(a + b) . sin b = \( - \frac{1}{3}\) cos(a + b) . cos b
\( \Leftrightarrow \frac{{\sin \left( {a + b} \right)\sin b}}{{\cos \left( {a + b} \right)\cos b}} = - \frac{1}{3}\)
⇔ tan(a + b) tan b = \(\frac{{ - 1}}{3}\).Câu 7:
Cho tam giác ABC, chứng minh rằng:
tan A + tan B + tan C = tan A . tan B . tan C (với điều kiện tam giác ABC không vuông);
 Xem đáp án
Xem đáp án
Vì tam giác ABC không vuông nên A, B, C khác \(\frac{\pi }{2}\), do đó tan A, tan B, tan C xác định.
Do A + B + C = π nên A + B = π – C, do đó tan(A + B) = tan(π – C) = tan(– C) = – tanC.
Mà \(\tan \left( {A + B} \right) = \frac{{\tan A + \tan B}}{{1 - \tan A\tan B}}\).
Khi đó \(\frac{{\tan A + \tan B}}{{1 - \tan A\,\tan B}} = - \tan C\)
⇔ tan A + tan B = – tan C . (1 – tan A . tan B)
⇔ tan A + tan B = – tan C + tan A . tan B . tan C
⇔ tan A + tan B + tan C = tan A . tan B . tan C.
Câu 8:
Cho tam giác ABC, chứng minh rằng:
\(\tan \frac{A}{2}.\tan \frac{B}{2} + \tan \frac{B}{2}.\tan \frac{C}{2} + \tan \frac{C}{2}.\tan \frac{A}{2} = 1\).
 Xem đáp án
Xem đáp án
Ta có \(\frac{{A + B + C}}{2} = \frac{\pi }{2}\), suy ra \(\frac{A}{2} + \frac{B}{2} = \frac{\pi }{2} - \frac{C}{2}\) nên \(\tan \left( {\frac{A}{2} + \frac{B}{2}} \right) = \cot \frac{C}{2}\)
\( \Leftrightarrow \frac{{\tan \frac{A}{2} + \tan \frac{B}{2}}}{{1 - \tan \frac{A}{2}.\tan \frac{B}{2}}} = \frac{1}{{\tan \frac{C}{2}}}\)
\( \Leftrightarrow \left( {\tan \frac{A}{2} + \tan \frac{B}{2}} \right)\tan \frac{C}{2} = 1 - \tan \frac{A}{2}.\tan \frac{B}{2}\)
\( \Leftrightarrow \tan \frac{A}{2}.\tan \frac{C}{2} + \tan \frac{B}{2}.\tan \frac{C}{2} + \tan \frac{A}{2}.\tan \frac{B}{2} = 1\)
\( \Leftrightarrow \tan \frac{A}{2}.\tan \frac{B}{2} + \tan \frac{B}{2}.\tan \frac{C}{2} + \tan \frac{C}{2}.\tan \frac{A}{2} = 1\).
Câu 9:
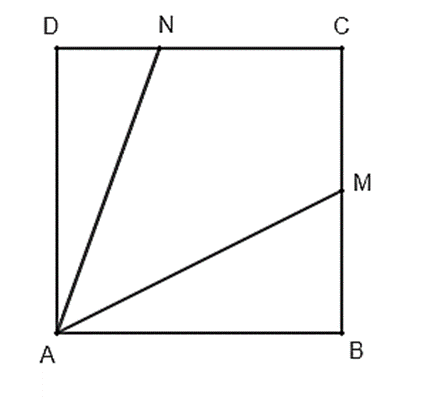
Trên một mảnh đất hình vuông ABCD, bác An đặt một chiếc đèn pin tại vị trí A chiếu chùm sáng phân kì sang phía góc C. Bác An nhận thấy góc chiếu sáng của đèn pin giới hạn bởi hai tia AM và AN, ở đó các điểm M, N lần lượt thuộc các cạnh BC, CD sao cho BM = \(\frac{1}{2}\)BC, DN = \(\frac{1}{3}\)DC (Hình 4).
Tính \(\tan \left( {\widehat {BAM} + \widehat {DAN}} \right)\).
 Xem đáp án
Xem đáp án
Trong tam giác vuông ABM, có \(\tan \widehat {BAM} = \frac{{BM}}{{BA}} = \frac{1}{2}\).
Trong tam giác vuông ADN, có \(\tan \widehat {DAN} = \frac{{DN}}{{AD}} = \frac{{DN}}{{DC}} = \frac{1}{3}\).
Do đó, \(\tan \left( {\widehat {BAM} + \widehat {DAN}} \right)\)\( = \frac{{\tan \widehat {BAM} + \tan \widehat {DAN}}}{{1 - \tan \widehat {BAM}.\tan \widehat {DAN}}}\)\( = \frac{{\frac{1}{2} + \frac{1}{3}}}{{1 - \frac{1}{2}.\frac{1}{3}}} = 1\).
Câu 10:
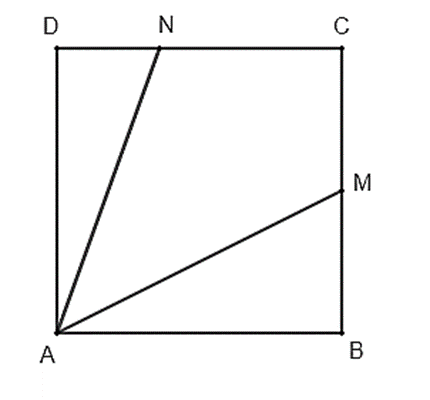
Trên một mảnh đất hình vuông ABCD, bác An đặt một chiếc đèn pin tại vị trí A chiếu chùm sáng phân kì sang phía góc C. Bác An nhận thấy góc chiếu sáng của đèn pin giới hạn bởi hai tia AM và AN, ở đó các điểm M, N lần lượt thuộc các cạnh BC, CD sao cho BM = \(\frac{1}{2}\)BC, DN = \(\frac{1}{3}\)DC (Hình 4).
Góc chiếu sáng của đèn pin bằng bao nhiêu độ?
 Xem đáp án
Xem đáp án
Từ câu a) ta có \(\tan \left( {\widehat {BAM} + \widehat {DAN}} \right)\) = 1 nên \(\widehat {BAM} + \widehat {DAN} = 45^\circ \).
Suy ra \(\widehat {MAN} = \widehat {BAD} - \left( {\widehat {BAM} + \widehat {DAN}} \right) = 90^\circ - 45^\circ = 45^\circ \).
Vậy góc chiếu sáng của đèn pin bằng 45°.
