15 câu hỏi trắc nghiệm thuộc Dạng 2. Tìm giao điểm của đường thẳng và mặt phẳng có đáp án

Câu 1:

Cho tứ diện ABCD. Gọi I, J lần lượt là các điểm nằm trên AB, AD với I là trung điểm AB và $A J = \frac{2}{3} A D$ . Tìm giao điểm của IJ và (BCD)

Xem đáp án

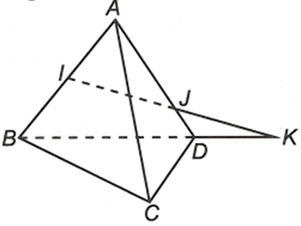
Cho tứ diện ABCD. Gọi I, J lần lượt là các điểm nằm trên AB, AD với I là trung điểm AB và Ạ = 2/3 AD (ảnh 1)

Trong tam giác ∆ABC có:

$\{\begin{cases} \frac{A I}{A B} = \frac{1}{2} \\ \frac{A J}{A D} = \frac{2}{3} \end{cases} \Rightarrow \frac{A I}{A B} \neq \frac{A J}{A D}$

Do đó IJ và BD không song song theo định lý Ta-lét.

Ta có $I J \subset (A B D)$

Lại có $(A B D) \cap (B C D) = B D$

Trong mặt phẳng (ABD) gọi $\{K\} = I J \cap B D$

Vậy

I J \cap (B C D) = \{K\}

Câu 2:

Cho tam giác BCD và điểm A không thuộc (BCD). Gọi K là trung điểm của AD và G là trọng tâm tam giác ABC. Tìm giao điểm của đường thẳng GK và (BCD)

Xem đáp án

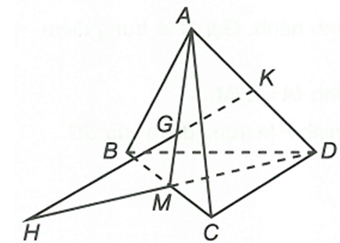
Cho tam giác BCD và điểm A không thuộc (BCD). Gọi K là trung điểm của AD và G là trọng tâm tam giác ABC. (ảnh 1)

Trong tam giác ∆AMD có $\{\begin{cases} \frac{A G}{A M} = \frac{2}{3} \\ \frac{A K}{A D} = \frac{1}{2} \end{cases} \Rightarrow \frac{A G}{A M} \neq \frac{A K}{A D}$

Nên GK và MD không song song theo định lý Ta-lét.

Ta có: $G K \subset (A M D)$ và $(A M D) \cap (B C D) = M D$ , suy ra trong $(A M D) : \{H\} = M D \cap G K$

Vậy $G K \cap (B C D) = \{H\}$

Câu 3:

Cho bốn điểm A, B, C, D không đồng phẳng. Gọi M, N lần lượt là trung điểm AC, BC. Trên đoạn BD lấy điểm P sao cho BP = 2PD.

a) Tìm giao điểm của CD và (MNP)

Xem đáp án

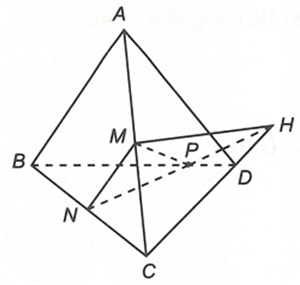
Cho bốn điểm A, B, C, D không đồng phẳng. Gọi M, N lần lượt là trung điểm AC, BC. Tìm giao điểm của CD và (MNP) (ảnh 1)

a) Trong ∆BCD có $\{\begin{cases} \frac{B N}{N C} = 1 \\ \frac{B P}{P D} = 2 \end{cases} \Rightarrow \frac{B N}{N C} \neq \frac{B P}{P D}$

Do đó NP và CD không song song theo định lý Ta-lét.

Ta có $C D \subset (B C D)$ và $(B C D) \cap (M N P) = N P$

Trong $(B C D) : C D \cap N P = \{H\}$

Vậy

C D \cap (M N P) = \{H\}

Câu 4:

b) Tìm giao tuyến của hai mặt phẳng (MNP) và (ACD)

Xem đáp án

b) Xét hai mặt phẳng (MNP) và (ACD) có $M \in (M N P) \cap (A C D) (1)$

Lại có $\{\begin{cases} H \in N P \subset (M N P) \Rightarrow H \in (M N P) \\ H \in C D \subset (A C D) \Rightarrow H \in (A C D) \end{cases} \Rightarrow H \in (M N P) \cap (A C D) (2)$

Từ (1) và (2) suy ra $M H = (M N P) \cap (A C D)$

Câu 5:

Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M là trung điểm của SC.

a) Tìm giao điểm I của AM với (SBD). Chứng minh IA = 2.IM

Xem đáp án

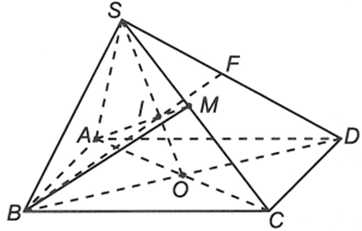
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M là trung điểm của SC. a) Tìm giao điểm I của AM với (SBD). Chứng minh IA = 2IM (ảnh 1)

a) Trong mặt phẳng (ABCD) gọi $A C \cap B D = \{O\}$

Ta có $A M \subset (S A C)$ ; (SAC) và (SBD) có S chung

Lại có $\{\begin{cases} O \in A C \subset (S A C) \Rightarrow O \in (S A C) \\ O \in B D \subset (S B D) \Rightarrow O \in (S B D) \end{cases} \Rightarrow O \in (S A C) \cap (S B D)$

Nên $S O = (S A C) \cap (S B D)$

Trong mặt phẳng $(S A C) : \{I\} = A M \cap S O$

Vậy $A M \cap (S B D) = \{I\}$

Xét ∆SAC có AM, SO là hai đường trung tuyến nên I là trọng tâm ∆SAC, suy ra theo tính chất trọng tâm ta có AI = 2IM

Câu 6:

b) Tìm giao điểm F của SD với (ABM). Chứng minh F là trung điểm của SD.

Xem đáp án

b) Ta có (SBD) và (ABM) có B chung

Lại có $\{\begin{cases} I \in S O \subset (S B D) \Rightarrow I \in (S B D) \\ I \in A M \subset (A B M) \Rightarrow I \in (A B M) \end{cases} \Rightarrow I \in (S B D) \cap (A B M)$

Nên $B I = (S B D) \cap (A B M)$

Trong mặt phẳng $(S B D) : \{F\} = B I \cap S D$

Vậy $\{F\} \in (A B M) \cap (S B D)$

Xét ∆SBD có SI = 2.OI và O là trung điểm BD nên I là trọng tâm ∆SBD.

Suy ra BF là trung tuyến ∆SBD

Vậy F là trung điểm SD.

Câu 7:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của SA, SB. Điểm H thuộc đoạn SD thỏa mãn $\frac{S H}{S D} = \frac{3}{4}$

a) Tìm giao điểm của NH và (ABCD)

Xem đáp án

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của SA, SB. a) Tìm giao điểm của NH và (ABCD) (ảnh 1)

a) Trong ∆SBD có $\{\begin{cases} \frac{S H}{S D} = \frac{3}{4} \\ \frac{S N}{S B} = \frac{1}{2} \end{cases} \Rightarrow \frac{S H}{S D} \neq \frac{S N}{S B}$

Do đó NH và BD không song song theo định lý Ta-lét

Ta có $N H \subset (S B D)$ và $(S B D) \cap (A B C D) = B D$

Trong mặt phẳng $(S B D) : \{I\} = N H \cap B D$

Vậy $N H \cap (A B C D) = \{I\}$

Câu 8:

b) Tìm giao điểm của đường thẳng SC và mặt phẳng (HMN)

Xem đáp án

b) Trong mặt phẳng (ABCD) có $A C \cap B D = \{O\}$

Trong mặt phẳng (SBD) có $S O \cap N H = \{P\}$

Ta có $S C \subset (S A C)$ ; (SAC) và (HMN) có M chung

Lại có $\{\begin{cases} P \in N H \subset (H N M) \Rightarrow P \in (H N M) \\ P \in S O \subset (S A C) \Rightarrow P \in (S A C) \end{cases} \Rightarrow P \in (H N M) \cap (S A C)$

Nên $M P = (S A C) \cap (H N M)$

Trong (SAC) gọi $\{R\} = M P \cap S C$ . Vậy $S C \cap (H N M) = \{R\}$

Câu 9:

Cho tứ diện ABCD có M, N lần lượt là các điểm thuộc cạnh BC và BD sao cho MN không song song CD. Gọi K là giao điểm của MN và (ACD). Khẳng định nào sau đây đúng?

A. K là giao của CM và DN

B. K là giao MN và AC

C. K là giao của MN và AD

D. K là giao của MN và CD

Xem đáp án

Đáp án D

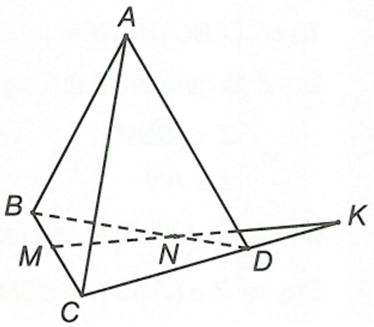
Cho tứ diện ABCD có M, N lần lượt là các điểm thuộc cạnh BC và BD sao cho MN không song song CD. (ảnh 1)

Trong (BCD) có $M N \cap C D = \{K\} \Rightarrow$ K là giao điểm của MN và (ACD)

Câu 10:

Cho hình chóp S.ABC. Gọi M, N lần lượt là hai điểm thuộc các cạnh AC, BC sao cho MN không song song với AB. Gọi K là giao điểm của đường thẳng MN và (SAB). Khẳng định nào sau đây đúng?

A. K là giao điểm của hai đường thẳng MN với AB

B. K là giao điểm của hai đường thẳng AM với BN

C. K là giao điểm của hai đường thẳng BN với AM

D. K là giao điểm của hai đường thẳng AN với BM

Xem đáp án

Đáp án A

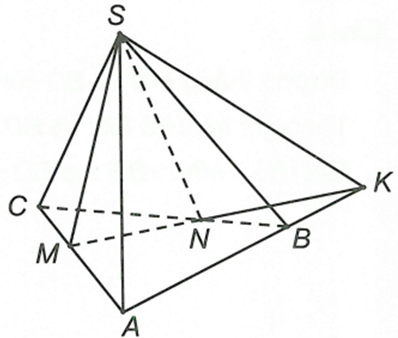
Cho hình chóp S.ABC. Gọi M, N lần lượt là hai điểm thuộc các cạnh AC, BC sao cho MN không song song với AB. (ảnh 1)

Ta có MN, AB đồng phẳng nên gọi $\{K\} = M N \cap A B$

Câu 11:

Cho hình chóp S.ABCD. Gọi M là điểm trên cạnh AB (M khác A, B), N là điểm trên cạnh SC (N khác S, C). Giao điểm của MN và (SBD) là

A. giao điểm của đường thẳng MN với SB

B. giao điểm của đường thẳng MN với SD

C. giao điểm của đường thẳng MN với BD

D. giao điểm của đường thẳng MN với đường thẳng SI với I là giao điểm của BD và CM

Xem đáp án

Đáp án D

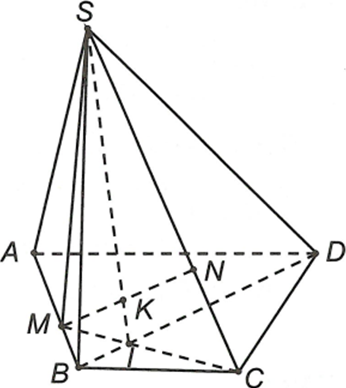
Cho hình chóp S.ABCD. Gọi M là điểm trên cạnh AB (M khác A, B), N là điểm trên cạnh SC (N khác S, C). (ảnh 1)

Gọi I là giao điểm của BD và CM.

Ta có MN, $S I \subset (S M C)$ , gọi $\{K\} = M N \cap S I$

Suy ra giao điểm của MN và (SBD) là giao điểm cùa đường thẳng MN với đường thẳng SI

Câu 12:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, K lần lượt là trung điểm của CD, CB, SA. Cặp đường thẳng nào sau đây cắt nhau?

A. SO và KC

B. MN và SB

C. KM và SC

D. MN và SA

Xem đáp án

Đáp án A

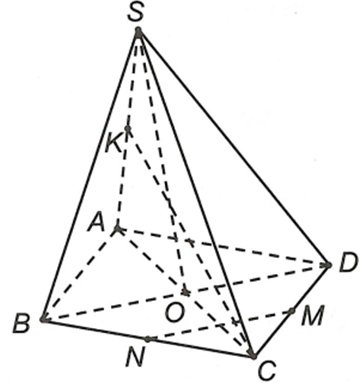
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, K lần lượt là trung điểm của CD, CB, SA. Cặp đường thẳng nào sau đây cắt nhau? (ảnh 1)

SO và KC cắt nhau vì cùng nằm trong mặt phẳng (SAC)

Câu 13:

Cho hình chóp S.ABC. Gọi M, N lần lượt là hai điểm thuộc vào các cạnh AC, BC sao cho MN không song song AB. Gọi Z là giao điểm đường AN và (SBM). Khẳng định nào sau đây đúng?

A. Z là giao điểm của hai đường thẳng AM với BN

B. Z là giao điểm của hai đường thẳng SN với AM

C. Z là giao điểm của hai đường thẳng MN với AB

D. Z là giao điểm của hai đường thẳng AN với BM

Xem đáp án

Đáp án D

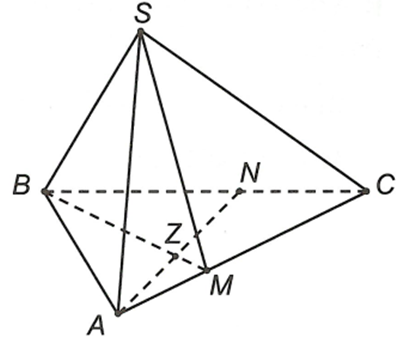
Cho hình chóp S.ABC. Gọi M, N lần lượt là hai điểm thuộc vào các cạnh AC, BC sao cho MN không song song AB. (ảnh 1)

Ta có $(A B C) \cap (S M B) = B M$

Do Z là giao điểm đường AN và (SBM)

$\Rightarrow \{\begin{cases} Z \in (S B M) \\ Z \in A N \end{cases} (1)$

Mà $A N \subset (A B C) \Rightarrow Z \in (A B C)$

Suy ra $Z \in (A B C) \cap (S B M) = B M (2)$

Từ (1) và (2) suy ra Z là giao điểm của hai đường thẳng AN và BM

Câu 14:

Cho hình chóp S.ABCD có đáy ABCD là một tứ giác (AB không song song với CD). Gọi M là trung điểm của SD, N là điểm nằm trên cạnh SB sao cho . Giao điểm của MN với (ABCD) là điểm K. Cách xác định điểm K nào đúng nhất trong bốn phương án sau?

A. K là giao điểm của MN với SD

B. K là giao điểm của MN với BC

C. K là giao điểm của MN với AB

D. K là giao điểm của MN với BD

Xem đáp án

Đáp án D

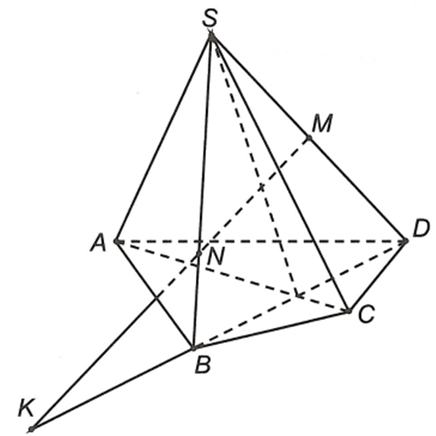
Cho hình chóp S.ABCD có đáy ABCD là một tứ giác (AB không song song với CD). Gọi M là trung điểm của SD, N (ảnh 1)

Đường thẳng MN và BD cùng nằm trong mặt phẳng (SBD)

Theo giả thiết thì MN và BD không song song.

Gọi $\{K\} = M N \cap B D$ mà $B D \subset (A B C D) \Rightarrow \{K\} = M N \cap (A B C D)$

Câu 15:

Cho hình chóp S.ABCD, đáy là hình thang có đáy lớn AB. Gọi O là giao của AC với BD, M là trung điểm SC. Giao điểm của đường thẳng AM và mp (SBD) là

A. I, với

\{I\} = A M \cap B C

B. I, với

\{I\} = A M \cap S O

C. I, với

\{I\} = A M \cap S B

D. I, với

\{I\} = A M \cap S C

Xem đáp án

Đáp án B

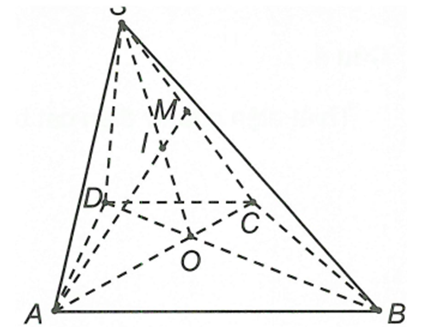
Cho hình chóp S.ABCD, đáy là hình thang có đáy lớn AB. Gọi O là giao của AC với BD, M là trung điểm SC. (ảnh 1)

Do Am, SO cùng nằm trong mặt phẳng (SAC)

Gọi $\{I\} = A M \cap S O$

Mà $S O \subset (S B D)$ nên $\{I\} = A M \cap (S B D)$

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập chuyên đề toán 11 Bài 1: Đại cương về đường thẳng và mặt phẳng có đáp án

Dạng 2. Tìm giao điểm của đường thẳng và mặt phẳng có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương