13 câu hỏi trắc nghiệm thuộc Dạng 3: Tìm thiết diện tạo bời một mặt phẳng và hình chóp. Chứng minh ba điểm thẳng hàng có đáp án

Bài tập chuyên đề toán 11 Bài 1: Đại cương về đường thẳng và mặt phẳng có đáp án

Dạng 3: Tìm thiết diện tạo bời một mặt phẳng và hình chóp. Chứng minh ba điểm thẳng hàng có đáp án

616 lượt thi
13 câu hỏi
60 phút

Danh sách câu hỏi

Câu 1:

Cho tứ diện ABCD. Gọi I, J lần lượt là các điểm nằm trên AB, AD sao cho BD và IJ không song song. Tìm thiết diện tạo bởi (CU) và hình chóp

Xem đáp án

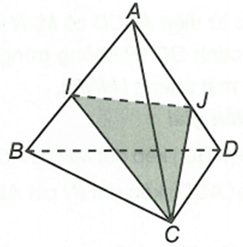
Cho tứ diện ABCD. Gọi I, J lần lượt là các điểm nằm trên AB, AD sao cho BD và IJ không song song. (ảnh 1)

Ta có

$(C I J) \cap (A B D) = I J (C I J) \cap (A B C) = I C (C I J) \cap (A C D) = C J$

Vậy thiết diện cần tìm là ∆CIJ

Câu 2:

Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AB. Gọi M, N lần lượt là trung điểm của SB và SC.

a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC)

Xem đáp án

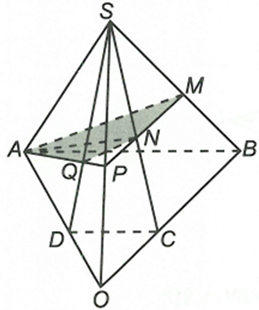
Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AB. Gọi M, N lần lượt là trung điểm của SB và SC. a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC) (ảnh 1)

a) Trong mặt phẳng (ABCD): $\{O\} = A D \cap B C$

Ta có (SAD) và (SBC) có S chung

Lại có $\{\begin{cases} O \in A D \subset (S A D) \Rightarrow O \in (S A D) \\ O \in B C \subset (S B C) \Rightarrow O \in (S B C) \end{cases} \Rightarrow O \in (S A D) \cap (S B C)$

Nên $S O = (S A D) \cap (S B C)$

Câu 3:

b) Tìm thiết diện của hình chóp với mặt phẳng (AMN)

Xem đáp án

b) Trong mặt phẳng (SOB) có $\{P\} = S O \cap M N$ và trong (SOA) gọi $\{Q\} = A P \cap S D$

Khi đó ta có

$\begin{array}{l} (S B C) \cap (A M N) = M N \\ (S C D) \cap (A M N) = Q N \\ (S A D) \cap (A M N) = A Q \\ (S A B) \cap (A M N) = A M \end{array}$

Vậy thiết diện của tứ diện cắt bởi mặt phẳng (AMN) là tứ giác AMNQ

Câu 4:

Cho tứ diện ABCD có M, N lần lượt là trung điểm của AB, CD và P là một điểm thuộc cạnh BC (P không trùng trung điểm cạnh BC). Tìm thiết diện của tứ diện cắt bởi mặt phẳng (MNP).

Xem đáp án

Cho tứ diện ABCD có M, N lần lượt là trung điểm của AB, CD và P là một điểm thuộc cạnh BC (P không trùng trung điểm cạnh BC). (ảnh 1)

Trong mp (ABC) kéo dài MP và AC cắt nhau tại I.

Trong mp (ACD) kéo dài IN cắt AD tại Q

Ta có

$\begin{array}{l} (A B C) \cap (M N P) = M P \\ (B C D) \cap (M N P) = P N \\ (A C D) \cap (M N P) = N Q \\ (A B D) \cap (M N P) = Q M \end{array}$

Vậy thiết diện của tứ diện cắt bởi mặt phẳng (MNP) là tứ giác MNPQ

Câu 5:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P là các điểm lần lượt trên các cạnh CB, CD, SA. Tìm thiết diện của hình chóp cắt bởi mặt phẳng (MNP)

Xem đáp án

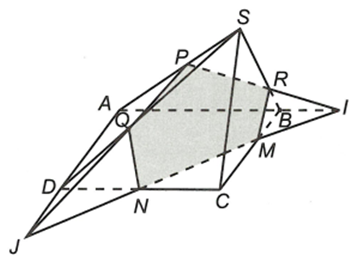
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P là các điểm lần lượt trên các cạnh CB, CD, SA. (ảnh 1)

Trong mặt phẳng (ABCD) gọi $\{I\} = M N \cap A B; \{J\} = M N \cap A D$

Trong (SAD) gọi $\{Q\} = S D \cap P J$

Trong (SAB) gọi $\{R\} = S B \cap P I$

Khi đó, dễ dàng chứng minh được M, N, Q, P, R lần lượt là giao điểm của (MNP) với các cạnh BC, CD, SD, SA, SB.

Do đó thiết diện cần tìm là ngũ giác MNQPR

Câu 6:

Cho hình chóp S.ABCD (AB và CD không song song) và M là điểm nằm trong ∆SCD. Xác định thiết diện của hình chóp cắt bởi mặt phẳng (ABM)

Xem đáp án

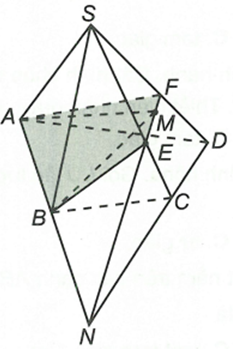
Cho hình chóp S.ABCD (AB và CD không song song) và M là điểm nằm trong ∆SCD. Xác định thiết diện của hình chóp cắt bởi mặt phẳng (ABM) (ảnh 1)

Trong (ABCD) gọi $\{N\} = A B \cap C D$

Trong (SCD) gọi $\{E\} = M N \cap S C; \{F\} = M N \cap S D$

Khi đó, dễ dàng chứng minh được E, F lần lượt là giao điểm của (ABM) với SC, SD.

Do đó thiết diện cần tìm là tứ giác ABEF.

Câu 7:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Trong mặt phẳng (ABCD) vẽ đường thẳng d đi qua A và không song song với các cạnh của hình bình hành. Trên cạnh SC lấy điểm M. Tìm thiết diện của hình chóp khi cắt bởi mặt phẳng (M,d).

Xem đáp án

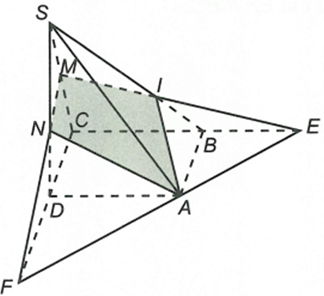
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Trong mặt phẳng (ABCD) vẽ đường thẳng d đi qua A và không song song với các cạnh của hình bình hành. (ảnh 1)

Trong (ABCD) gọi $\{E\} = d \cap B C; \{F\} = d \cap C D$

Trong (SBC) gọi $\{I\} = M E \cap S B$

Trong (SCD) gọi $\{N\} = M F \cap S D$

Khi đó, ta có tứ giác AIMN là thiết diện cần tìm.

Câu 8:

Cho hình chóp S.ABCD. M là điểm thuộc cạnh SB (không trùng với S và B). Thiết diện tạo bởi (AMD) và hình chóp S.ABCD là

A. ngũ giác

B. tứ giác

C. tam giác

D. không có

Xem đáp án

Đáp án B

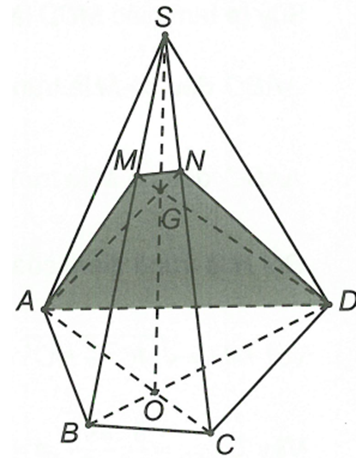
Cho hình chóp S.ABCD. M là điểm thuộc cạnh SB (không trùng với S và B). Thiết diện tạo bởi (AMD) và hình chóp S.ABCD là (ảnh 1)

Ta có $(S B D) \cap (S A C) = S O; (A D M) \cap (S B D) = M D$

Gọi $M D \cap S O = \{G\} \Rightarrow (S A C) \cap (A D M) = A G$

Gọi $\{N\} = A G \cap S C$

=> Thiết diện khi cắt bởi hình chóp là tứ giác ADNM

Câu 9:

Cho hình chóp S.ABCD, đáy ABCD là hình bình hành, cắt hình chóp bằng mặt phẳng (MNP), trong đó M, N, P lần lượt là trung điểm các cạnh AB, AD, SC. Thiết diện nhận được là

A. ngũ giác

B. tứ giác

C. tam giác

D. không có

Xem đáp án

Đáp án A

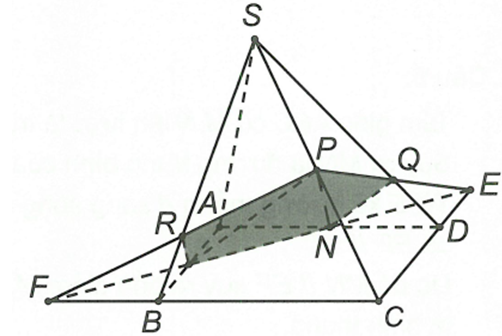
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành, cắt hình chóp bằng mặt phẳng (MNP), trong đó M, N, P lần lượt là trung điểm (ảnh 1)

Trong mp (ABCD) gọi $\{E\} = C D \cap M N; \{Q\} = P E \cap S D$

Gọi $\{F\} = B C \cap M N; \{R\} = P F \cap S B$ . Suy ra thiết diện tao bởi mặt phẳng (MNP) với hình chóp là ngũ giác MNQPR.

Câu 10:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J lần lượt là trung điểm của SB và SD. Thiết diện của mặt phẳng (AIJ) với hình chóp là

A. tam giác

B. ngũ giác

C. tứ giác

D. lục giác

Xem đáp án

Đáp án C

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J lần lượt là trung điểm của SB và SD. (ảnh 1)

Gọi $\{O\} = A C \cap B D; \{K\} = S O \cap I J; \{H\} = A K \cap S C$

Khi đó thiết diện của mặt phẳng (AIJ) với hình chóp S.ABCD là tứ giác AIHJ

Câu 11:

Cho tứ diện ABCD và ba điểm M, N, P lần lượt nằm trên các cạnh AB, AC, AD (không trùng với các đỉnh). Thiết diện của tứ diện cắt bởi mặt phẳng (MNP) là

A. một đoạn thẳng

B. một tứ giác

C. một tam giác đều

D. một tam giác

Xem đáp án

Đáp án D

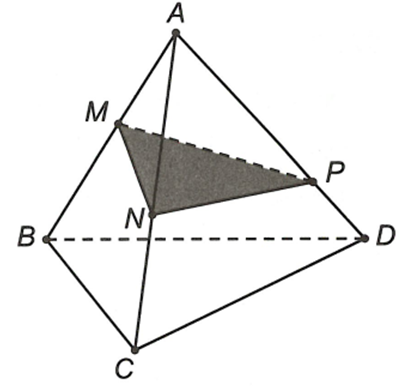
Cho tứ diện ABCD và ba điểm M, N, P lần lượt nằm trên các cạnh AB, AC, AD (không trùng với các đỉnh). (ảnh 1)

Thiết diện của tứ diện cắt bởi mặt phẳng (MNP) là tam giác MNP

Câu 12:

Cho tứ diện đều ABCD có cạnh bằng a. Gọi G là trọng tâm tam giác ABC. Mặt phẳng (GCD) cắt tứ diện theo một thiết diện có diện tích

A. $\frac{a^{2} \sqrt{3}}{2}$

B. $\frac{a^{2} \sqrt{2}}{4}$

C. $\frac{a^{2} \sqrt{2}}{6}$

D. $\frac{a^{2} \sqrt{3}}{4}$

Xem đáp án

Đáp án B

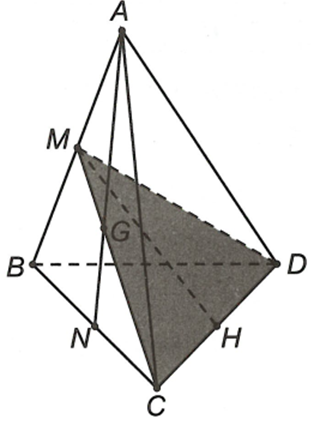
Cho tứ diện đều ABCD có cạnh bằng a. Gọi G là trọng tâm tam giác ABC. Mặt phẳng (GCD) cắt tứ diện theo một thiết diện có diện tích (ảnh 1)

Gọi M,N lần lượt là trung điểm của AB, BC suy ra $A N \cap M C = \{G\}$

(GCD) cắt đường thẳng AB tại điểm M.

Suy ra tam giác MCD là thiết diện của mặt phẳng (GCD) và tứ diện ABCD.

∆ABD đều có M là trung điểm AB suy ra $M D = \frac{a \sqrt{3}}{2}$

∆ABC đều có M là trung điểm AB suy ra $M C = \frac{a \sqrt{3}}{2}$

Gọi H là trung điểm CD $\Rightarrow M H ⊥ C D \Rightarrow S_{Δ M C D} = \frac{1}{2} . M H . C D$

Với $M H = \sqrt{M C^{2} - H D^{2}} = \sqrt{M C^{2} - \frac{C D^{2}}{4}} = \frac{a \sqrt{2}}{2}$

Vậy $S_{Δ M C D} = \frac{1}{2} . \frac{a \sqrt{2}}{2} . a = \frac{a^{2} \sqrt{2}}{4}$

Câu 13:

Cho tứ diện ABCD; gọi M, N lần lượt là trung điểm các cạnh AB và AC, E là điểm trên cạnh CD với ED = 3EC. Thiết diện tạo bởi mặt phẳng (MNE) và tứ diện ABCD

A. tam giác MNE

B. tứ giác MNEF với F là điểm bất kì trên cạnh BD

C. hình bình hành MNEF với F là điểm trên cạnh BD mà EF // BC

D. hình thang MNEF với F là điểm trên cạnh BD mà EF // BC

Xem đáp án

Đáp án D

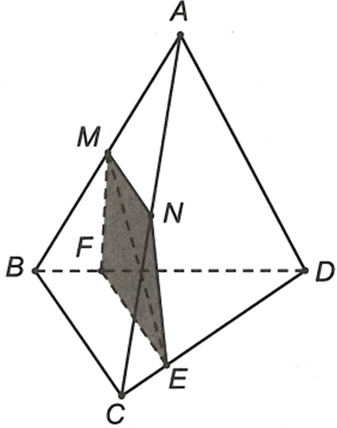
Cho tứ diện ABCD; gọi M, N lần lượt là trung điểm các cạnh AB và AC, E là điểm trên cạnh CD với ED = 3EC (ảnh 1)

Tam giác ABC có M, N lần lượt là trung điểm của AB, AC.

Suy ra MN là đường trung bình của tam giác ABC => MN // BC

Từ E kẻ đường thẳng d song song với BC và cắt BD tại F

=> EF // BC.

Do đó MN // EF suy ra bốn điểm M, N, E, F đồng phẳng và MNEF là hình thang

Vây hình thang MNEF là thiết diện cần tìm

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập chuyên đề toán 11 Bài 1: Đại cương về đường thẳng và mặt phẳng có đáp án

Dạng 3: Tìm thiết diện tạo bời một mặt phẳng và hình chóp. Chứng minh ba điểm thẳng hàng có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương