Trắc nghiệm Toán 11 Bài 1: Đại cương về đường thẳng và mặt phẳng (có đáp án)
Trắc nghiệm Toán 11 Bài 1: Đại cương về đường thẳng và mặt phẳng (phần 1) (có đáp án)
-
1803 lượt thi
-
28 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
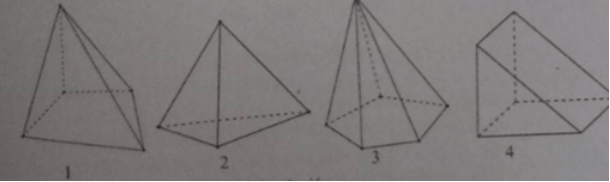
Trong phát biểu sau đây, phát biểu nào đúng?
 Xem đáp án
Xem đáp án
Phương án A sai vì mặt đáy có thể không là tam giác.
Phương án B đúng vì theo định nghĩa
Phương án C sai vì theo định nghĩa mặt bên của hình chóp luôn là tam giác
Phương án D sai vì số cạnh bên bằng số mặt bên trong khi các mặt hình chóp gồm các mặt bên và mặt đáy.
Có thể giải thích D sai vì xét với hình chóp tam giác số cạnh bên bằng 3 nhưng số mặt bằng 4.
Đáp án B
Câu 2:
Một mặt phẳng hoàn toàn được xác định nếu biết điều nào sau đây?
 Xem đáp án
Xem đáp án
Phương án A sai vì nếu ba điểm đó thẳng hàng thì chưa thể xác định được mặt phẳng.
Phương án B sai vì nếu điểm đó nằm trên đường thẳng thì ta chưa thể xác định được.
Phương án C đúng (theo tính chất thừa nhận 2)
Phương án D sai vì hai đường thẳng có thể trùng nhau.
Chọn đáp án C.
Câu 3:
Trong các phát biểu sau, phát biểu nào đúng?
 Xem đáp án
Xem đáp án
Phương án A sai vì nếu hai mặt phẳng trùng nhau thì chúng có vô số đường thẳng chung.
Phương án B sai vì nếu hai mặt phẳng có hai điểm chung thì chúng có chung một đường thẳng.
Phương án C đúng vì hai mặt phẳng có điểm chung thì chúng có thể cắt nhau hoặc trùng nhau.
Phương án D sai vì hai mặt phẳng đáy của hình hộp thì không có điểm chung.
Chọn đáp án C
Câu 4:
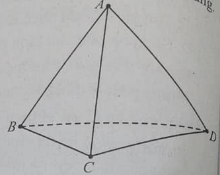
Cho hình tứ diện ABCD, phát biểu nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Phương án A sai vì nếu AC cắt BD thì 4 điểm A, B, C, D đồng phẳng, điều này mẫu thuẫn với A, B, C, D là 4 đỉnh của một tứ diện.
Phương án B đúng vì nếu chúng có điểm chung thì A, B, C, D không thể là 4 đỉnh của một tứ diện
Phương án C sai vì nếu có một mặt phẳng chứa AD và BC thì 4 điểm A, B, C, D đồng phẳng, điều này mâu thuẫn với A, B, C, D là 4 đỉnh của một tứ diện.
Phương án D sai.
Chọn phương án B.
Câu 5:
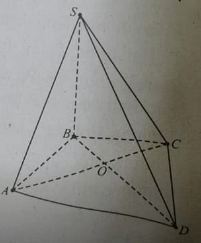
Cho hình chóp S.ABCD, O là giao điểm của AC và BD, phát biểu nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Phương án A đúng vì O là giao điểm của AC và BD nên O là điểm chung của (SAC) và (SBD). Hơn nữa, S là điểm chung của (SAC) và (SBD).
Phương án B sai vì giao tuyến của hai mặt phẳng không thể là điểm
Phương án C sai vì SD và BC không cắt nhau
Phương án D sai vì AC và SD không cắt nhau
Chọn đáp án A.
Câu 6:
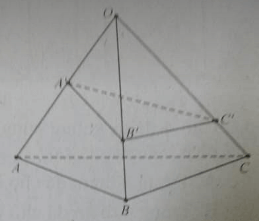
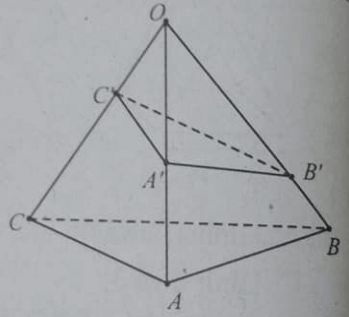
Cho hình chóp O.ABC, A’ là trung điểm của OA; các điểm B’, C’ tương ứng thuộc các cạnh OB, OC và không phải là trung điểm của các cạnh này. Phát biểu nào sau đây là đúng.
 Xem đáp án
Xem đáp án
* Phương án A sai vì A’ không phải là điểm chung của (OBC) và (A’B’C’).
* Phương án B sai vì
Xét giao tuyến của 2 mp (ABC ) và (OC'A') có:
A chung
C chung
Do đó, giao tuyến của mp(ABC) và mp (OC'A') là AC
+ Phương án C sai vì:
Trong mp (OAB), A’B’ không song song với AB nên sẽ cắt AB, do vậy (ABC) và (A’B’C’) có điểm chung
+ Phương án D đúng vì M là giao điểm của AC và A’C’ nên M là điểm chung của (ABC) và (A’B’C’),
Tương tự N là điểm chung của (ABC) và (A’B’C’).
Vì vậy MN là giao tuyến của (ABC) và (A’B’C’).
Chọn đáp án D.
Câu 7:
Trong các phát biểu sau, phát biểu nào đúng?
 Xem đáp án
Xem đáp án
Đáp án B
Hình tứ diện có 4 mặt, 6 cạnh và 4 đỉnh
Câu 8:
Số cạnh của hình chóp tam giác là:
 Xem đáp án
Xem đáp án
Đáp án C
Hình chóp tam giác có 4 mặt, 6 cạnh và 4 đỉnh
Câu 10:
Cho 4 điểm không cùng thuộc một mặt phẳng. Trong các phát biểu sau đây, phát biểu nào là sai?
 Xem đáp án
Xem đáp án
+ Phương án A đúng vì nếu có ba điểm thẳng hàng ( giả sử là A; B; C) thì bốn điểm đã cho luôn thuộc mặt phẳng chứa điểm D còn lại và đường thẳng AB. (mâu thuẫn giả thiết)
+ Phương án C đúng . Số mặt phẳng đi qua 3 trong 4 điểm đã cho là:
+ Phương án D đúng. Số đoạn thẳng nối 2 điểm trong 4 điểm đã cho là:
Đáp án B
Câu 11:
Có duy nhất một mặt phẳng đi qua
 Xem đáp án
Xem đáp án
Đáp án D
+ Phương án A sai vì nếu 2 đường thẳng đó trùng nhau thì có vô số mặt phẳng đi qua 2 đường thẳng đó.
+ Phương án B sai vì nếu điểm đó thuộc đường thẳng đã cho thì có vô số mặt phẳng đi qua điểm và đường thẳng đã cho.
+ Phương án C sai vì nếu có 2 trong ba điểm đó trùng nhau hoặc cả 3 điểm đó trùng nhau thì có vô số mặt phẳng thỏa mãn.
Câu 14:
Cho 4 điểm không đồng phẳng. Số mặt phẳng phân biệt mà mỗi mặt phẳng đi qua ba trong bốn điểm đó là:
 Xem đáp án
Xem đáp án
Đáp án D
Vì 4 điểm không đồng phẳng nên chọn 3 điểm bất kì từ 4 điểm ta xác định được 1 mặt phẳng
Do đó, số mặt phẳng phân biệt mà mỗi mặt phẳng đi qua ba trong bốn điểm đó là:
Câu 15:
Cho 6 đường thẳng đôi một cắt nhau. Hỏi xác định được nhiểu nhất bao nhiêu mặt phẳng đi qua 2 trong số các đường thẳng đã cho
 Xem đáp án
Xem đáp án
Đáp án D
Lấy 2 đường thẳng cắt nhau ta xác định được 1 mặt phẳng
Do đó, số mặt phẳng nhiều nhất đi qua 2 trong số 6 đường thẳng đã cho là;
Câu 20:
Cho hình chóp O.ABC, A’ là trung điểm của OA, B’, C’ tương ứng thuộc các cạnh OB, OC và không phải là trung điểm của các cạnh này. Phát biểu nào sau đây là đúng?
 Xem đáp án
Xem đáp án
+ Trong mặt phẳng (OAC) , có:
C’ không là trung điểm của OC nên A’C’ không song song với AC
Do đó AC và A’C’ cắt nhau.
+ Phương án D sai vì CB, C’B’ cắt nhau tại 1 điểm thuộc mặt phẳng (OBC)
Đáp án A
Câu 21:
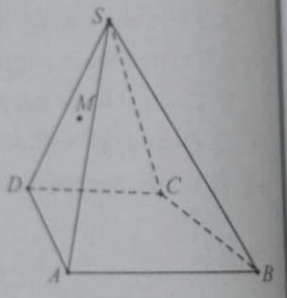
Cho hình chóp S.ABCD, M là điểm nằm trong tam giác SAD. Phát biểu nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án A
Đáp án A đúng
Đáp án B sai vì giao điểm của BD và (SAC) là giao điểm của BD và AC
Đáp án C sai vì CM không cắt SA
Đáp án D sai vì DM cắt mặt phẳng (SBC)tại giao điểm của DM và giao tuyến của hai mặt phẳng (SAD) và(SBC).
Câu 22:
Cho hình chóp S.ABCD, các điểm A’, B’, C’ lần lượt thuộc các cạnh SA, SB, SC. Phát biểu nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án B
Ta có: (SAB) (A’B’C’) = A’B’
(SBC) (A’B’C’) = B’C’
Gọi O là giao điểm của AC và BD
Trong mặt phẳng (SAC) gọi I là giao điểm của A’C’ và SO
Trong mặt phẳng (SBD) gọi D’ là giao điểm của B’I và SD
Khi đó ta có: (SCD) (A’B’C’) = C’D’
(SAD) (A’B’C’) = A’D’
Do đó thiết diện của mặt phẳng (A’B’C’) với hình chóp S.ABCD là tứ giác A’B’C’D’.
Câu 23:
Cho hình chóp S.ABCD, đáy là hình bình hành ABCD, các điểm M, N lần lượt thuộc các cạnh AB, SC. Phát biểu nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án C
Trong mặt phẳng (ABCD) gọi I là giao điểm của MC và BD
Trong mặt phẳng (SMC) gọi H là giao điểm của SI và MN
Khi đó H SI (SBD); H MN
Do đó H là giao điểm của MN và mặt phẳng (SBD)
Câu 24:
Cho hình chóp S. ABCD, đáy là hình bình hành ABCD, các điểm M, N lần lượt thuộc các cạnh AB, SC. Phát biều nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án B
Trong mặt phẳng (ABCD) gọi I là giao điểm của MD và BC
Trong mặt phẳng (SBC) gọi K là giao điểm của IN và SB
Khi đó ta có: (MND) (SAB) = KM
(MND) (ABCD) = MD
(MND) (SBC) = KN
(MND) (SCD) = ND
Vậy thiết diện của mặt phẳng (MND) với hình chóp là tứ giác NDMK.
Đáp án B
Câu 25:
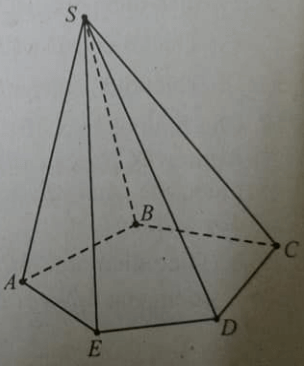
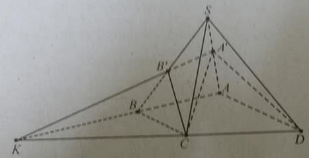
Cho hình chóp S.ABCD, đáy là hình thang ABCD, AD // BC và AD > BC, A’ là trung điểm của SA, B’ thuộc cạnh SB và không phải là trung điểm của SB. Phát biểu nào sau đây là đúng?
Hình vẽ như sau:
 Xem đáp án
Xem đáp án
Đáp án D
Ta có: (A’B’C) (SAB) = A’B’
(A’B’C) (SBC) = B’C
(A’B’C) (SCD) = CD
(A’B’C) (SAD) = A’D
Vậy thiết diện của mặt phẳng (A’B’C) với hình chóp là tứ giác A’B’C’D.
Đáp án D
Câu 26:
Cho hình chóp S.ABCD, đáy là hình thang ABCD, AD // BC và AD > BC, A’ là trung điểm của SA, B’ thuộc cạnh SB và không phải là trung điểm của SB. Phát biểu nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án A
Theo câu 25 ta có: (A’B’C) (SAB) = A’B’
(A’B’C) (ABCD) = CD
(SAB) (ABCD) = AB
Do đó ba đường thẳng A’B’; CD và AB đồng quy.
Câu 27:
Cho ba đường thẳng a, b, c đôi một cắt nhau và không đồng phẳng. số giao điểm của ba đường thẳng là:
 Xem đáp án
Xem đáp án
Đáp án C
Vì ba đường thẳng a, b, c đôi một cắt nhau và không đồng phẳng nên ba
đường thẳng đó đồng quy với nhau tại 1 điểm.