Trắc nghiệm Toán 11 Bài 1: Vectơ trong không gian (phần 1) (có đáp án)
-
1387 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
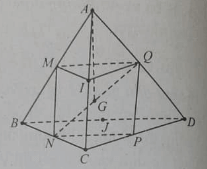
Cho tứ diện ABCD. Các điểm M và N lần lượt là trung điểm của AB và CD. Lấy hai điểm P và Q lần lượt thuộc AD và BC sao cho và , với m khác 1. Vecto bằng:
 Xem đáp án
Xem đáp án
Có thể loại các phương án A, B và D vì các cặp ba vecto , () và () đều không đồng phẳng.
Phương án C đúng vì :
Đáp án C
Câu 2:
Cho tứ diện ABCD. Gọi M, N, P, và Q lần lượt là trung điểm của AB, BC, CD, và DA.
Vecto cùng với hai vecto nào sau đây là ba vecto đồng phẳng?
 Xem đáp án
Xem đáp án
Cách 1:
Ta có: M và N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác ABC
suy ra: MN// AC và (1)
Tương tự: QP là đường trung bình của tam giác ACD nên QP // AC và (2)
Từ (1) và (2) suy ra: tứ giác MNPQ là hình bình hành (có các cạnh đối song song và bằng nhau)
* Cách 2:
Tam giác ABC có MN là đường trung bình nên MN // AC và
Do đó, 3 vecto đồng phẳng
Đáp án C
Câu 3:
Cho tứ diện ABCD. Gọi M, N, P, và Q lần lượt là trung điểm của AB, BC, CD, và DA.
Vecto cùng với hai vecto nào sau đây là ba vecto không đồng phẳng?
 Xem đáp án
Xem đáp án
Đáp án A
Câu 4:
Cho ba vecto . Điều kiện nào sau đây không kết luận được ba vecto đó đồng phẳng.
 Xem đáp án
Xem đáp án
Nếu hai trong ba vecto đó cùng hướng thì ba vecto đồng phẳng.
Nếu hai trong ba vecto đó không cùng hướng thì chưa thể kết luận được ba vecto đó đồng phẳng.
Ví dụ. Cho tứ diện ABCD có M, N lần lượt là trung điểm của AB; AC. Khi đó, vecto không cùng hướng với hai vecto . Nhưng 3 vecto trên vẫn đồng phẳng.
Đáp án C
Câu 5:
Ba vecto không đồng phẳng nếu?
 Xem đáp án
Xem đáp án
Đáp án C
Theo định nghĩa sự đồng phẳng của 3 vecto: 3 vecto đồng phẳng
nếu giá của chúng cùng song song với 1 mặt phẳng.
Câu 6:
Cho tứ diện ABCD với G là trọng tâm và các điểm M, N, P, Q, I, J lần lượt là trung điểm của các cạnh AB, BC, CD, AD, AC, BD.
Những vecto khác bằng nhau là:
 Xem đáp án
Xem đáp án
Đáp án D
Ta xét từng phương án:
+) Ta có: MN là đường trung bình của tam giác ABC nên MN // = 1/2 AC
Mà I là trung điểm của AC nên ta có IC = 1/2 AC
Do đó
Nên ba vecto không phải là ba vecto bằng nhau, đáp án A sai.
+) Ba vecto không phải là ba vecto bằng nhau vì chúng không cùng hướng nên đáp án B sai.
+) Ta có MQ là đường trung bình của tam giác ABD
NP là đường trung bình của tam giác CBD
Suy ra MQ //= NP (1)
Lại có: (quy tắc trừ hai vecto) (2)
Từ (1) và (2) suy ra
Nên C sai, D đúng.
Câu 7:
Cho tứ diện ABCD với G là trọng tâm và các điểm M, N, P, Q, I, J lần lượt là trung điểm của các cạnh AB, BC, CD, AD, AC, BD.
bằng:
 Xem đáp án
Xem đáp án
Ta có N là trung điểm của BC
Suy ra
Lại có: (Q là trung điểm của AD)
Do đó (1)
Tạ lại có G là trọng tâm của tứ diện ABCD nên G là trung điểm của NQ (tính chất trọng tâm của tứ diện) (2)
Từ (1) và (2) suy ra .
Đáp án A
Câu 8:
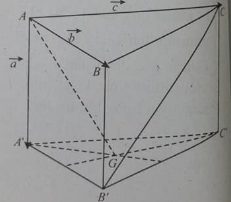
Cho hình lăng trụ ABC.A’B’C’ với G là trọng tâm của tam giác A’B’C’. Đặt
Vecto bằng:
 Xem đáp án
Xem đáp án
( áp dụng quy tắc hình bình hành)
Đáp án B
Câu 9:
Cho hình lăng trụ ABC.A’B’C’ với G là trọng tâm của tam giác A’B’C’. Đặt
Vecto bằng:
 Xem đáp án
Xem đáp án
Gọi M là trung điểm của B'C'
Theo tính chất trọng tâm tam giác và trung điểm của đoạn thẳng ta có :
Do đó:
Đáp án D
Câu 10:
Tứ diện OABC có các cạnh OA, OB, OC đôi một vuông góc và đều có độ dài là l. Gọi M là trung điểm của các cạnh AB. Góc giữa hai vecto và bằng:
 Xem đáp án
Xem đáp án
Tam giác OAB vuông tại O (OA OB)
Theo định lý Py-ta-go ta có:
Tương tự BC =
Ta có: OM là trung tuyến của tam giác OAB vuông tại O
Nên OM = 1/2AB =
Đáp án D