22 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 11 Bài 3: Cấp số cộng (phần 1) (có đáp án)

Câu 1:

Cho cấp số cộng có 8 số hạng. Số hạng đầu bằng 3 số hạng cuối bằng 24. Tính tổng các số hạng này

A. 105

B. 27

C. 108

D. 111

Xem đáp án

Ta có u1 = 3; u8 = 24, n = 8.

Tổng của 8 số hạng này là:

$S_{8} = \frac{n . (u_{1} + u_{8})}{2} = \frac{8 . (3 + 24)}{2} = 108$

Đáp án C

Câu 2:

Cho các dãy số sau, dãy số nào là cấp số cộng

A. Dãy số $(a_{n})$ xác định bởi : $\{\begin{cases} a_{1} = 1 \\ a_{n + 1} = a_{n} + 3 n \end{cases} v ớ i n \geq 1$

B. Dãy số $(b_{n})$ xác định bởi : $\{\begin{cases} b_{1} = 3 \\ b_{n + 1} = b_{n} - 3 \end{cases} v ớ i n \geq 1$

C. Dãy số $(c_{n})$ xác định bởi : $c_{n} = \sqrt{n + 2} v ớ i n \geq 1$

D. Dãy số $(d_{n})$ xác định bởi : $\{\begin{cases} d_{1} = 4 \\ d_{n + 1} = d_{n} + n \end{cases} v ớ i n \geq 1$

Xem đáp án

Xét phương án B :

Ta có: $b_{n + 1} = b_{n} - 3 \Leftrightarrow b_{n + 1} - b_{n} = - 3$ ( một số không đổi)

Do đó, đây là cấp số cộng có công sai d = -3.
Đáp án là B

Câu 3:

Cho 4 số lập phương thành cấp số cộng. Tổng của chúng bằng 22. Tổng các bình phương của chúng bằng 166. Tổng các lập phương của chúng bằng :

A. 22

B. 166

C. 1752

D. 1408

Xem đáp án

Gọi 4 số lập thành cấp số cộng là x - 3d; x- d; x + d; x + 3d.

Bốn số này lập thành cấp số cộng với công sai là 2d.

Theo giả thiết ta có:

$\{\begin{cases} x - 3 d + x - d + x + d + x + 3 d = 22 \\ {(x - 3 d)}^{2} + {(x - d)}^{2} + {(x + d)}^{2} + {(x + 3 d)}^{2} = 166 \end{cases} \Leftrightarrow \{\begin{cases} 4 x = 22 \\ 4 x^{2} + 20 d^{2} = 166 \end{cases} \Leftrightarrow \{\begin{cases} x = \frac{11}{2} \\ d = \pm \frac{3}{2} \end{cases}$

Vậy 4 số đó là 1,4,7,10 hoặc 10,7,4,1

Tổng các lập phương của chúng: 13+43+73+ 103=1408

Đáp án là D

Câu 4:

Trong mặt phẳng toạ độ, cho đồ thị (d) của hàm số y= 4x-5.

Với mỗi số nguyên dương, gọi An là giao điểm của(d) và đường thẳng x=n. Xét dãy số ( $u_{n}$ ) với $u_{n}$ là tung độ của điểm An. Tính $u_{1} + . . . + u_{15} .$

A. 405

B. 305

C. 205

D. 105

Xem đáp án

Dễ thấy $u_{n} = 4 n - 5$

Ta có: $u_{n + 1} = 4 (n + 1) - 5 = 4 n - 1$

$\Rightarrow u_{n + 1} = u_{n} + 4, \forall n \geq 1$

Suy ra $(u_{n})$ là một cấp số cộng với công sai là $d = 4$

Ta có: $u_{1} = 4.1 - 5 = - 1; u_{15} = 4.15 - 5 = 55$

Vậy $u_{1} + u_{2} + ... + u_{15} = S_{15} = \frac{15}{2} (u_{1} + u_{15}) = \frac{15}{2} (- 1 + 55) = 405$

Đáp án là A

Câu 5:

Tìm x biết 1+3 +5+...+x =64

A. 9

B. 11

C. 15

D. 17

Xem đáp án

Vế trái: 1 + 3+ 5+ .. + x là tổng của cấp số cộng có $u_{1} = 1; d = 2; u_{n} = x$

$S_{n} = \frac{n . [2 + (n - 1) . 2]}{2} = 64 \Leftrightarrow 2 n + 2 n^{2} - 2 n = 128 \Leftrightarrow 2 n^{2} = 128 \Leftrightarrow n^{2} = 64 \Rightarrow n = 8$

Khi đó, $x = u_{8} = 1 + 7 . 2 = 15$

Đáp án C.

Câu 6:

Cho hai cấp số cộng $(u n) : 4, 7, 10, 13, 16, . . . v à (v n)$ :1,6,11,16,21,...Hỏi trong 100 số hạng đầu tiên của mỗi cấp số cộng , có bao nhiêu số hạng chung?

A. 10

B. 20

C. 30

D. 40

Xem đáp án

Ta có $u_{n} = 4 + (n - 1) .3 = 3 n + 1$ với $1 \leq n \leq 100$

$v_{k} = 1 + (k - 1) .5 = 5 k - 4$ với $1 \leq k \leq 100$

Để một số là số hạng chung của hai cấp số cộng ta phải có

$3 n + 1 = 5 k - 4 \Leftrightarrow 3 n = 5 (k - 1)$

$\Rightarrow n ⋮ 5$ tức là $n = 5 t$ với $t \in ℤ$

Vì $1 \leq n \leq 100$ nên $1 \leq t \leq 20$ . Do đó có 20 số hạng chung của hai dãy số.

Chọn đáp án B

Câu 7:

Mặt sàn tầng một cuả một ngôi nhà cao hơn mặt sân 0,5m. Cầu thang đi từ tầng 1 lên tầng 2 gồm 21 bậc mỗi bậc cao 18 cm. Độ cao của tầng hai so với mặt sân là:

A. 4,10m

B. 4,28m

C. 1,89m

D. 1,8m

Xem đáp án

Độ cao của tầng hai so với mặt sàn tầng một là: 0, 18. 21= 3,78 (m)

Độ cao tầng hai so với mặt sàn của sân là h = 0,5 + 3,78 = 4,28m

Vậy ta có độ cao tầng 2 bằng 4,28m

Đáp án B

Câu 8:

Công sai của cấp số cộng (un) thoả mãn : $\{\begin{cases} u_{1} + u_{5} - u_{3} = 10 \\ u_{1} + u_{6} = 17 \end{cases} l à$

A. 0

B. -1

C. -2

D. -3

Xem đáp án

Chọn D

Ta giải hệ:

$\begin{array}{l} \{\begin{cases} u_{1} + u_{1} + 4 d - u_{1} - 2 d = 10 \\ u_{1} + u_{1} + 5 d = 17 \end{cases} \\ \Leftrightarrow \{\begin{cases} u_{1} + 2 d = 10 \\ 2 u_{1} + 5 d = 17 \end{cases} \\ \Leftrightarrow \{\begin{cases} u_{1} = 16 \\ d = - 3 \end{cases} \end{array}$

Câu 9:

Số hạng đầu tiên của cấp số cộng dương (un) thoả mãn :

$\{\begin{cases} u_{7} - u_{3} = 8 \\ u_{2} u_{7} = 75 \end{cases}$

A. 2

B. 3

C. 4

D. 5

Xem đáp án

Ta có:

$\{\begin{cases} u_{7} - u_{3} = 8 \\ u_{2} u_{7} = 75 \end{cases} \Leftrightarrow \{\begin{cases} u_{1} + 6 d - u_{1} - 2 d = 8 \\ (u_{1} + d) . (u_{1} + 6 d) = 75 \end{cases} \Leftrightarrow \{\begin{array}{l} 4 d = 8 \\ u_{1}^{2} + 7 u_{1} d + 6 d^{2} = 75 \end{array} \Leftrightarrow \{\begin{cases} d = 2 \\ u_{1}^{2} + 14 u_{1} + 24 = 75 \end{cases} \Rightarrow u_{1} = 3; u_{1} = - 17$

Vì $u_{1} > 0$ nên $u_{1} = 3$

Chọn B

Câu 10:

Xác định số đo góc nhỏ nhất của một tứ giác lồi, biết rằng số đo 4 góc lập thành một cấp số cộng và góc lớn nhất bằng 5 lần góc nhỏ nhất.

A. 30°

B. 45°

C. 15°

D. 60°

Xem đáp án

Chọn A

Gọi d=2a là công sai. Bốn số phải tìm là:

A=(x-3a); B=(x-a); C=(x+a); D=(x+3a).

Tổng số đo 4 góc của 1 tứ giác bằng $360^{0}$

Ta có hệ phương trình:

$\Leftrightarrow \{\begin{cases} 4 x = 360^{0} \\ x + 3 a = 5 x - 15 a \end{cases} \Leftrightarrow \{\begin{array}{l} x = 90^{0} \\ 4 x = 18 a \end{array} \Leftrightarrow \{\begin{cases} x = 90^{0} \\ a = 20^{0} \end{cases}$

Số đo góc nhỏ nhất là : 90 - 3.20 = 30

Câu 11:

Xen vào giữa hai số 4 và 40 bốn số để được một cấp số cộng có công sai lớn hơn 3. Tìm tổng 4 số đó.

A. 88

B. 92

C. 128

D. 132

Xem đáp án

Chọn A

Nếu xen 4 số vào giữa hai số để được một cấp số cộng thì cấp số cộng đó có 6 số hạng.

Theo đầu bài

Ta có: $u_{1} = 4; u_{6} = 40$

$\begin{array}{l} \Rightarrow 40 = 4 + 5. d \\ \Rightarrow d = 7, 2 \end{array}$

Vậy 4 số thêm vào là:11,2; 18,4; 25,6; 32,8

Tổng 4 số đó là: 11, 2+ 18,4+ 25,6 + 32,8 = 88

Câu 12:

Người ta trồng 3003 cây theo hình tam giác như sau: hàng thứ nhất có 1 cây, hàng thứ 2 có 2 cây, hàng thứ 3 có 3 cây,...Vậy có tất cả bao nhiêu hàng?

A. 75

B. 76

C. 77

D. 78

Xem đáp án

Chọn C

Số cây mỗi hàng lập thành cấp số cộng.

Trong đó, $u_{1} = 1, d = 1$

Tổng số cây trồng theo kiểu trên là

$S_{n} = \frac{n . [2 . 1 + (n - 1) . 1]}{2} = 3003 \Leftrightarrow \frac{n . (n + 1)}{2} = 3003 \Leftrightarrow n^{2} + n - 6006 = 0 \Rightarrow n = 77$

Câu 13:

Giá tiền công khoan giếng ở cơ sở A được tính như sau: giá của mét khoan đầu tiên là 8000 đồng và kể từ mét khoan thứ hai, giá của mỗi mét sau tăng lên 500 đồng so với giá của mét khoan ngay trước nó. Vậy muốn khoan 20 mét thì mất bao nhiêu đồng?

A. 200000 đồng

B. 255000 đồng

C. 285000 đồng

D. 315000 đồng

Xem đáp án

Chọn B

Gọi $u_{n}$ là giá của mét khoan thứ n.

Ta thấy ( $u_{n}$ ) lập thành cấp số cộng với $u_{1} = 8000; d = 500$

Do đó, giá khi khoan 20 m là

$S_{20} = 20 . \frac{2.8000 + (20 - 1) . 500}{2} = 255 000$

Câu 14:

Cho một dãy số có các số hạng đầu tiên là 1,8,22,43...Hiệu của hai số hạng liên tiếp của dãy số đó lập thành một cấp số cộng: 7,14,21,...,7n. Số 35351 là số hạng thứ bao nhiêu của dãy số đã cho?

A. 57

B. 80

C. 101

D. 200

Xem đáp án

Chọn C

Theo đề bài ta có:

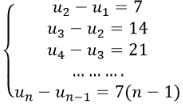
Cộng vế với vế các phương trình của hệ ta được:

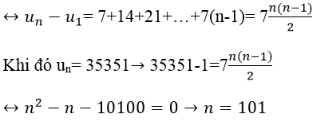
Câu 15:

Cho phương trình: $x^{3} + 3 x^{2} - (24 + m) x - 26 - n = 0 .$ Tìm hệ thức liên hệ giữa m và n để 3 nghiệm phân biệt $x_{1}, x_{2}, x_{3}$ lập thành một cấp số cộng

A. 3m =n

B. m =n

C. m =3n

D. m + n =0

Xem đáp án

Chọn B

Vì ba nghiêm phân biệt $x_{1}, x_{2}, x_{3}$ lập thành một cấp số cộng nên ta đặt : $x_{1} = x_{0} - d, x_{2} = x_{0}, x_{3} = x_{0} + d (d \neq 0)$

Theo giả thiết Ta có: x3+3x2 – (24+m)x – 26- n= (x – x1)(x-x2)(x-x3)

=(x-xo+d)(x-xo)(x-xo-d)= x3 – 3xox2+ (3xo2-d2)x-xo3+ xod2 với mọi x.

Đồng nhất hai vế ta được:

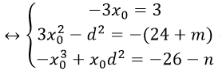
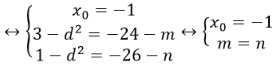
Vậy với m=n thì ba nghiệm phân biệt của phương trình lập thành một cấp số cộng

Câu 16:

Tìm m để phương trình $x^{3} - 3 x^{2} - 9 x + m = 0$ có ba nghiệm phân biệt lập thành cấp số cộng.

A. m = 16

B. m= 11

C. m= 13

D. m = 12

Xem đáp án

Chọn B.

Điều cần cần:

Giả sử phương trình có ba nghiệm phân biệt lập thành cấp số cộng.

Khi đó: $x_{1} + x_{3} = 2 x_{2},$

Lại có :

$\begin{array}{l} x_{1} + x_{2} + x_{3} = \frac{- b}{a} = 3 \\ \Rightarrow x_{2} = 1 \end{array}$

Thay vào phương trình ta được: 1³ – 3.1² – 9.1 + m =0

$\Leftrightarrow m = 11$

* Điều kiện đủ : Với m =11 phương trình trở thành :

$x^{3} - 3 x^{2} - 9 x + 11 = 0$

$\begin{array}{l} \Leftrightarrow (x - 1) (x^{2} - 2 x - 11) = 0 \\ \Leftrightarrow x_{1} = 1 - \sqrt{12}, \\ x_{2} = 1, \\ x_{3} = 1 + \sqrt{12} \end{array}$

Ba nghiệm này lập thành cấp số cộng.

Vậy m =11 là giá trị cần tìm.

Câu 17:

Phương trình $x^{4} - 2 (m + 1) x^{2} + 2 m + 1 = 0$ (1) có bốn nghiệm phân biệt lập thành cấp số cộng

A. m = 2 hoặc $m = - \frac{4}{9}$

B. m = 4 hoặc $m = - \frac{4}{9}$

C. m =4 hoặc m=-2

D.m = 3 hoặc m=-1

Xem đáp án

Chọn B

Đặt $t = x^{2}, t \geq 0$ .

Phương trình trở thành: $t^{2} - 2 (m + 1) t + 2 m + 1 = 0$ (2)

Phương trình (1) có bốn nghiệm phân biệt khi và chỉ khi PT (2) có hai nghiệm dương phân biệt t₂ > t₁ > 0 .

$\{\begin{matrix} Δ' > 0 \\ P > 0 \\ S > 0 \end{matrix}$

$\Leftrightarrow \{\begin{matrix} {(m + 1)}^{2} - (2 m + 1) > 0 \\ 2 m + 1 > 0 \\ 2 (m + 1) > 0 \end{matrix} \Leftrightarrow - \frac{1}{2} < m \neq 0$

Khi đó PT (2) có bốn nghiệm là: $- \sqrt{t_{2}}; - \sqrt{t_{1}}; \sqrt{t_{1}}; \sqrt{t_{2}}$

Bốn nghiệm này lập thành cấp số cộng khi :

$\begin{array}{l} \{\begin{matrix} - \sqrt{t_{2}} + \sqrt{t_{1}} = - 2 \sqrt{t_{1}} \\ - \sqrt{t_{1}} + \sqrt{t_{2}} = 2 \sqrt{t_{1}} \end{matrix} \\ \Leftrightarrow \sqrt{t_{2}} = 3 \sqrt{t_{1}} \\ \Leftrightarrow t_{2} = 9 t_{1} \end{array}$

Theo định lý viet thì : $\{\begin{matrix} t_{1} + t_{2} = 2 (m + 1) \\ t_{1} t_{2} = 2 m + 1 \end{matrix}$

$\begin{array}{l} \Rightarrow \{\begin{matrix} t_{1} + 9 t_{1} = 2 (m + 1) \\ t_{1} 9 t_{1} = 2 m + 1 \end{matrix} \\ \Leftrightarrow \{\begin{matrix} 10 t_{1} = 2 (m + 1) (*) \\ 9 t_{1}^{2} = 2 m + 1 (* *) \end{matrix} \end{array}$ .

Từ (*) suy ra: $5 t_{1} = m + 1 \Leftrightarrow m = 5 t_{1} - 1$ thay vào (**) ta được:

$\begin{array}{l} 9 t_{1}^{2} = 2 (5 t_{1} - 1) + 1 \\ \Leftrightarrow 9 t_{1}^{2} - 10. t_{1} + 1 = 0 \\ \Leftrightarrow [\begin{matrix} t_{1} = \frac{1}{9} \Rightarrow m = \frac{- 4}{9} \\ t_{1} = 1 \Rightarrow m = 4 \end{matrix} \end{array}$

Vậy m = 4 hoặc $m = - \frac{4}{9}$ là những giá trị cần tìm

Câu 18:

Một tam giác vuông có chu vi bằng 3 và độ dài các cạnh lập thành một cấp số cộng. Độ dài các cạnh của tam giác đó là:

A. $\frac{1}{2}; 1; \frac{3}{2} .$

B. $\frac{1}{3}; 1; \frac{5}{3} .$

C. $\frac{3}{4}; 1; \frac{5}{4} .$

D. $\frac{1}{4}; 1; \frac{7}{4} .$

Xem đáp án

Chọn C

Ba cạnh a, b, c ( a < b < c) của một tam giác theo thứ tự đó lập thành một cấp số cộng thỏa mãn yêu cầu thì:

$\begin{array}{l} \{\begin{cases} a^{2} + b^{2} = c^{2} \\ a + b + c = 3 \\ a + c = 2 b \end{cases} \\ \Leftrightarrow \{\begin{cases} a^{2} + b^{2} = c^{2} \\ 3 b = 3 \\ a + c = 2 b \end{cases} \\ \Leftrightarrow \{\begin{cases} a^{2} + b^{2} = c^{2} \\ b = 1 \\ a = 2 b - c = 2 - c \end{cases} . \end{array}$

Ta có

$a^{2} + b^{2} = c^{2} \to_{a = 2 - c}^{b = 1} {(2 - c)}^{2} + 1 = c^{2}$

$\begin{array}{l} \Leftrightarrow - 4 c + 5 = 0 \\ \Leftrightarrow c = \frac{5}{4} \Rightarrow \{\begin{cases} a = \frac{3}{4} \\ b = 1 \\ c = \frac{5}{4} \end{cases} . \end{array}$

Câu 19:

Một rạp hát có 30 dãy ghế, dãy đầu tiên có 25 ghế. Mỗi dãy sau có hơn dãy trước 3 ghế. Hỏi rạp hát có tất cả bao nhiêu ghế?

A. 1635

B. 1792

C. 2055

D. 3125

Xem đáp án

Chọn C

Số ghế của mỗi dãy (bắt đầu từ dãy đầu tiên) theo thứ tự đó lập thành một cấp số cộng có 30 số hạng có công sai d= 3 và u₁ =25

Tổng số ghế là

$\begin{array}{l} S_{30} = u_{1} + u_{2} + \dots + u_{30} \\ = \frac{30}{2} [2 u_{1} + (30 - 1) d] \\ = 2055 \end{array}$

Câu 20:

Bốn số hạng liên tiếp của một cấp số cộng biết tổng của chúng bằng 20 và tổng các bình phương của chúng bằng 120. Tính tổng của hai số hạng đầu tiên?

A. 6

B. 7

C. 5

D. 8

Xem đáp án

Chọn A

Giả sử bốn số hạng đó là $a - 3 x; a - x; a + x; a + 3 x$ với công sai là d =2x. Khi đó, ta có:

$\{\begin{matrix} (a - 3 x) + (a - x) + (a + x) + (a + 3 x) = 20 \\ {(a - 3 x)}^{2} + {(a - x)}^{2} + {(a + x)}^{2} + {(a + 3 x)}^{2} = 120 \end{matrix}$

$\Leftrightarrow \{\begin{matrix} 4 a = 20 \\ 4 a^{2} + 20 x^{2} = 120 \end{matrix} \Leftrightarrow \{\begin{matrix} a = 5 \\ x = \pm 1 \end{matrix}$

Vậy bốn số cần tìm là 2; 4; 6; 8.

Tổng của 2 số hạng đầu tiên là: 2+ 4= 6.

Câu 21:

Cho a, b, c theo thứ tự lập thành cấp số cộng, đẳng thức nào sau đây là đúng?

A. $a^{2} + c^{2} = 2 a b + 2 b c + 2 a c$

B. $a^{2} - c^{2} = 2 a b + 2 b c - 2 a c$

C. $a^{2} + c^{2} = 2 a b + 2 b c - 2 a c$

D. $a^{2} - c^{2} = 2 a b - 2 b c + 2 a c$

Xem đáp án

Chọn C

Để a; b; c theo thứ tự lập thành cấp số cộng khi và chỉ khi

$\begin{array}{l} b - a = c - b \\ \Leftrightarrow {(b - a)}^{2} = {(c - b)}^{2} \\ \Leftrightarrow b^{2} - 2 a b + a^{2} = c^{2} - 2 b c + b^{2} \\ \Leftrightarrow a^{2} - c^{2} = 2 a b - 2 b c \end{array}$

$\begin{array}{l} \Leftrightarrow a^{2} + c^{2} = 2 c^{2} + 2 a b - 2 b c \\ = 2 a b + 2 c (c - b) \\ = 2 a b + 2 c (b - a) \\ = 2 a b + 2 b c - 2 a c \end{array}$

Câu 22:

Tìm x biết $x^{2} + 1, x - 2,1 - 3 x$ lập thành cấp số cộng ;

A. $x = 4, x = 3$

B. $x = 2, x = 3$

C. $x = 2, x = 5$

D. $x = 2, x = 1$

Xem đáp án

Chọn B

Ta có: $x^{2} + 1, x - 2,1 - 3 x$ lập thành cấp số cộng

$\begin{array}{l} \Leftrightarrow x^{2} + 1 + 1 - 3 x = 2 (x - 2) \\ \Rightarrow x^{2} + 2 - 3 x = 2 x - 4 \\ \Leftrightarrow x^{2} - 5 x + 6 = 0 \\ \Leftrightarrow x = 2; x = 3 \end{array}$

Vậy x = 2; x = 3 là những giá trị cần tìm.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Toán 11 Bài 3: Cấp số cộng (có đáp án)

Trắc nghiệm Toán 11 Bài 3: Cấp số cộng (phần 1) (có đáp án)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương