27 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 11 Bài 3: Một số phương trình lượng giác thường gặp (phần 3) (có đáp án)

Câu 1:

Tập nghiệm của phương trình sinxcos2x = 1 là:

A. {-π/2+k2π;k∈Z}

B. {π/2+kπ;k∈Z}

C. {k2π;k∈Z}

D. ∅

Xem đáp án

Chọn D

Do -1≤sinx,cos2x≤1 nên sinxcos2x=1

+ Trường hợp 1:Sinx = cos2x = 1

Với sinx = 1 thì ta có:

$\cos 2 x = 1 - 2 \sin^{2} x = 1 - 2 . 1^{2} = - 1 \neq 1$ ( theo giả thiết) nên loại

+ Trường hợp 2: sinx = cos2x = -1

$\Leftrightarrow \{\begin{cases} \sin x = - 1 \\ \cos 2 x = - 1 \end{cases} \Leftrightarrow \{\begin{cases} x = - \frac{π}{2} + k 2 π \\ 2 x = π + k 2 π \end{cases} \Leftrightarrow \{\begin{cases} x = - \frac{π}{2} + k 2 π \\ x = \frac{π}{2} + k π \end{cases} \Leftrightarrow x = - \frac{π}{2} + k 2 π$

Câu 2:

Giá trị nhỏ nhất và lớn nhất của hàm số $y = \frac{2 \sin x + \cos x + 1}{\sin x - 2 \cos x + 3}$ lần lượt là:

A. – 1/2 và 2

B. 1/2 và 2

C. -2 và -1/2

D. -2 và 1/2

Xem đáp án

Chọn A

Ta có: $y = \frac{2 \sin x + \cos x + 1}{\sin x - 2 \cos x + 3}$

${(\sin x - 2 \cos x)}^{2} \leq (1^{2} + 2^{2}) . (\sin^{2} x + \cos^{2} x) = 5 \Rightarrow - \sqrt{5} \leq \sin x - 2 \cos x \leq \sqrt{5} \Rightarrow \sin x - 2 \cos x + 3 > 0 \forall x$

+ $y = \frac{2 \sin x + \cos x + 1}{\sin x - 2 \cos x + 3}$

$\Leftrightarrow$ y. (sinx - 2cosx + 3) = 2sinx + cosx + 1

$\Leftrightarrow$ (y-2) . sinx - (2y+ 1)cosx = 1 - 3y (*)

Để phương trình (*) có nghiệm điều kiện là:

${(y - 2)}^{2} + {(2 y + 1)}^{2} \geq {(1 - 3 y)}^{2} \Leftrightarrow y^{2} - 4 y + 4 + 4 y^{2} + 4 y + 1 \geq 1 - 6 y + 9 y^{2} \Leftrightarrow - 4 y^{2} + 6 y + 4 \geq 0 \Leftrightarrow \frac{- 1}{2} \leq y \leq 2$

Câu 3:

Giá trị lớn nhất của hàm số $y = 3 - \sqrt{2} (\sin x + \cos x)$ là:

A. 5

B. $3 + \sqrt{2}$

C. $3 - \sqrt{2}$

D. 3

Xem đáp án

Chọn A

dấu đẳng thức xảy ra khi

Câu 4:

Hàm số $y = \frac{1}{\sin x - \cos x}$ có tập xác định là:

A. ℝ\{kπ,k∈Z}

B. ℝ\{k2π,k∈Z}

C. ℝ\{π/2+kπ,k∈Z}

D. ℝ\{π/4+kπ,k∈Z}

Xem đáp án

Đáp án đúng là D

Giải thích

Hàm số xác định $\Leftrightarrow \sin x - \cos x \neq 0$

$\Leftrightarrow \sin x \neq \cos x$

$\Leftrightarrow \cos x \neq \cos (\frac{π}{2} - x)$

$\Leftrightarrow [\begin{array}{l} x \neq \frac{π}{2} - x + k 2 π \\ x \neq - \frac{π}{2} + x + k 2 π \end{array}$

$\Leftrightarrow x \neq \frac{π}{4} + k π$

Câu 5:

Hàm số $y = \sqrt{(3 - \sin 2 x)}$ có tập xác định là:

A. ℝ\{x│sin2x < 0}

B. ℝ\{k2π,k∈Z}

C. ℝ

D. Một tập hợp khác

Xem đáp án

Đáp án đúng: C

Giải thích:

Hàm số xác định $\Leftrightarrow 3 - \sin 2 x \geq 0$ $\Leftrightarrow \sin 2 x \leq 3$ (luôn đúng)

Vậy tập xác định của hàm số là R

Câu 6:

Chu kì của hàm số $y = \sin \frac{x}{2} + \cos x$ là:

A. 0

B. 2π

C. 4π

D. 6π

Xem đáp án

Chọn C

Giải thích:

Chu kì của hàm số $y_{1} = \sin \frac{x}{2}$ là $T_{1} = \frac{2 π}{|\frac{1}{2}|} = 4 π$

Chu kì của hàm số $y_{2} = \cos x$ là $T_{2} = 2 π$

Chu kì của hàm số $y = \sin \frac{x}{2} + \cos x = y_{1} + y_{2}$ là $B C N N (2; 4) . π = 4 π$ .

Câu 7:

Trong các hàm số sau, hàm nào là hàm số lẻ?

A. $y = x^{2} . c o s x$

B. y = sin2x

C. $y = \sin^{2} x$

D. y = cosx

Xem đáp án

Giải thích:

Xét phương án B:

TXĐ: $D = ℝ$

Giả sử $x \in D$ thì $- x \in D$

Ta có $f (- x) = \sin (- 2 x) = - \sin 2 x = - f (x)$

Vậy $\sin 2 x$ là hàm lẻ.

Chọn đáp án B.

Câu 8:

Phương trình $\sin^{2} x + 4 \sin x \cos x + 2 m \cos^{2} x = 0$ có nghiệm khi:

A. m ≥ 2

B. m ≤ 2

C. m ≥ 4

D. m ≤ 4

Xem đáp án

Chọn B

$\sin^{2} x + 4 \sin x \cos x + 2 m \cos^{2} x = 0$
$\Leftrightarrow \frac{1 - \cos 2 x}{2} + 2 \sin 2 x + 2 m . \frac{1 + \cos 2 x}{2} = 0$
$\Leftrightarrow \frac{1 - \cos 2 x + 2 m + 2 m \cos 2 x}{2} + 2 \sin 2 x = 0$
$\Leftrightarrow (2 m - 1) \cos 2 x + 4 \sin 2 x + 2 m + 1 = 0$

Phương trình có nghiệm $\Leftrightarrow {(2 m - 1)}^{2} + 4^{2} \geq {(2 m + 1)}^{2}$

$\Leftrightarrow 4 m^{2} - 4 m + 1 + 16 \geq 4 m^{2} + 4 m + 1$
$\Leftrightarrow - 8 m \geq - 16$

$\Leftrightarrow m \leq 2$ .

Câu 9:

Giá trị x∈(0,π) thoả mãn điều kiện $\cos^{2} x + \sin x - 1 = 0$ là:

A. x= π/2

B. x = π/4

C. x = -π/2

D. x = 2π/3

Xem đáp án

Đáp án đúng: A

Giải thích

$\cos^{2} x + \sin x - 1 = 0$
$\Leftrightarrow - \sin^{2} x + \sin x = 0$
$\Leftrightarrow \sin x (- \sin x + 1) = 0$
$\Leftrightarrow [\begin{array}{l} \sin x = 0 \\ - \sin x + 1 = 0 \end{array}$
$\Leftrightarrow [\begin{array}{l} x = k π \\ x = \frac{π}{2} + k 2 π \end{array}$

Vì $x \in (0; π)$ nên $x = \frac{π}{2}$

Chọn đáp án A.

Câu 10:

Giá trị nhỏ nhất của hàm số $y = 3 \sin x + 4 \cos x + 5$ là:

A. 0

B. -2

C. 5

D. -1

Xem đáp án

Chọn A

$y = 3 \sin x + 4 \cos x + 5$
$\Leftrightarrow 3 \sin x + 4 \cos x = y - 5$

Để phương trình có nghiệm thì $3^{2} + 4^{2} \geq {(y - 5)}^{2}$

$\Leftrightarrow 25 \geq y^{2} - 10 y + 25$
$\Leftrightarrow y^{2} - 10 y \leq 0$
$\Leftrightarrow 0 \leq y \leq 10$

Vậy giá trị nhỏ nhất của hàm số là 0.

Câu 11:

Giá trị nhỏ nhất và lớn nhất của hàm số $y = \frac{2 \sin x + \cos x + 3}{- \sin x + 2 \cos + 4}$ lần lượt là:

A. 1/2 và 1

B. 1/2 và 2

C. 2/11 và 1

D. 2/11 và 2

Xem đáp án

Xét $- \sin x + 2 \cos x + 4 = 0$ $\Leftrightarrow - \sin x + 2 \cos x = - 4$

Ta thấy ${(- 1)}^{2} + 2^{2} < 4^{2}$ nên phương trình vô nghiệm.

Do đó $- \sin x + 2 \cos x + 4 \neq 0$ .

Như vậy, $y = \frac{2 \sin x + \cos x + 3}{- \sin x + 2 \cos x + 4}$

$\Leftrightarrow y (- \sin x + 2 \cos x + 4) = 2 \sin x + \cos x + 3$

$\Leftrightarrow \sin x (2 + y) + \cos x (1 - 2 y) = 4 y - 3$

Để phương trình có nghiệm thì ${(2 + y)}^{2} + {(1 - 2 y)}^{2} \geq {(4 y - 3)}^{2}$

$\Leftrightarrow 5 y^{2} + 5 \geq 16 y^{2} - 24 y + 9$

$\Leftrightarrow 11 y^{2} - 24 y + 4 \leq 0$

$\Leftrightarrow \frac{2}{11} \leq y \leq 2$

Chọn đáp án D.

Câu 12:

Tập nghiệm của phương trình sin3x +1 = 0 là:

A. {-π/2+kπ,k∈Z}

B. {-π/2+k2π,k∈Z}

C. {-π/6+k2π,k∈Z}

D. {-π/6+k 2π/3,k∈Z}

Xem đáp án

Đáp án đúng: D

Giải thích:

$\sin 3 x + 1 = 0 \Leftrightarrow \sin 3 x = - 1$

$\Leftrightarrow 3 x = \frac{- π}{2} + k 2 π$

$\Leftrightarrow x = \frac{- π}{6} + k \frac{2 π}{3}$

Câu 13:

Tập nghiệm của phương trình tanx + cotx -2 = 0 là:

A. {-π/4+kπ,k∈Z}

B. {π/4+kπ,k∈Z}

C. {±π/4+k2π,k∈Z}

D. ∅

Xem đáp án

Đáp án đúng: B

Giải thích

ĐKXĐ: $\{\begin{cases} \sin x \neq 0 \\ \cos x \neq 0 \end{cases} \Leftrightarrow x \neq k \frac{π}{2}$

$\tan x + \cot x - 2 = 0$

$\Leftrightarrow \tan x + \frac{1}{\tan x} - 2 = 0$
$\Leftrightarrow \tan^{2} x - 2 \tan x + 1 = 0$

$\Leftrightarrow \tan x = 1$

$\Leftrightarrow x = \frac{π}{4} + k π$ (thỏa mãn ĐKXĐ)

Câu 14:

Hàm số $y = \frac{\tan 2 x}{1 - \tan x}$ có tập xác định là:

A. ℝ

B. $ℝ \ {π / 4 + k π / 2, k \in Z}$

C. $ℝ \ {π / 2 + k π, k \in Z}$

D. $\emptyset$

Xem đáp án

ĐKXĐ: $\{\begin{cases} \cos 2 x \neq 0 \\ \tan x \neq 1 \end{cases}$

$\Leftrightarrow \{\begin{cases} 2 x \neq \frac{π}{2} + k π \\ x \neq \frac{π}{4} + k π \end{cases} \Leftrightarrow \{\begin{cases} x \neq \frac{π}{4} + k \frac{π}{2} \\ x \neq \frac{π}{4} + k π \end{cases} \Leftrightarrow x \neq \frac{π}{4} + k \frac{π}{2}$

Chọn đáp án B.

Câu 15:

Tập nghiệm của phương trình $2 \sin^{2} x - \sin 2 x = 0$ là:

A. {π/4+kπ,kπ,k∈Z}

B. {kπ,k∈Z}

C. {π/4+k2π,k∈Z}

D. {k2π,k∈Z}

Xem đáp án

Đáp án đúng: A

Giải thích

$2 \sin^{2} x - \sin 2 x = 0$
$\Leftrightarrow 1 - \cos 2 x - \sin 2 x = 0$
$\Leftrightarrow \cos 2 x + \sin 2 x = 1$
$\Leftrightarrow \frac{1}{\sqrt{2}} \cos 2 x + \frac{1}{\sqrt{2}} \sin 2 x = \frac{1}{\sqrt{2}}$
$\Leftrightarrow \cos (\frac{π}{4} - 2 x) = \cos (\frac{π}{4})$
$\Leftrightarrow [\begin{array}{l} \frac{π}{4} - 2 x = \frac{π}{4} + k 2 π \\ \frac{π}{4} - 2 x = \frac{- π}{4} + k 2 π \end{array}$

$\Leftrightarrow [\begin{array}{l} x = - k π \\ x = \frac{π}{4} - k π \end{array} \Leftrightarrow [\begin{array}{l} x = l π \\ x = \frac{π}{4} + l π \end{array}$

Câu 16:

Tập nghiệm của phương trình $2 \cos^{2} 5 x + 3 \cos 5 x - 5 = 0$ thuộc khoảng (0;π) là:

A. {0,π/5}

B. {2π/5,4π/5}

C. {π/5,2π/5}

D. {2π/5,3π/5,4π/5}

Xem đáp án

Chọn B

Đặt $\cos 5 x = t$ , phương trình trở thành:

$2 t^{2} + 3 t - 5 = 0$
$\Leftrightarrow [\begin{array}{l} t = 1 \\ t = \frac{- 5}{2} \end{array}$

Với t=1 thì $\cos 5 x = 1 \Leftrightarrow 5 x = k 2 π \Leftrightarrow x = \frac{k 2 π}{5}$

Với $t = \frac{- 5}{2}$ thì $\cos x = \frac{- 5}{2}$ (vô lí vì $- 1 \leq \cos x \leq 1$ )

Mà $x \in (0; π)$ nên các giá trị thỏa mãn là $\frac{2 π}{5}; \frac{4 π}{5}$ .

Câu 17:

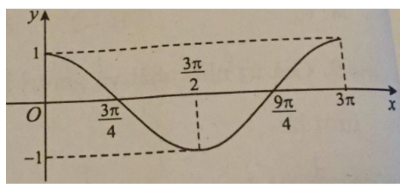
Hình bên là một phần của đồ thị hàm số nào sau đây?

A. $y = \cos \frac{2 x}{3}$

B. $y = \sin \frac{2 x}{3}$

C. $y = c o s \frac{3 x}{2}$

D. $y = \sin \frac{3 x}{2}$

Xem đáp án

Theo đồ thị, chu kì của hàm số là $3 π$ nên loại đáp án C, D

Thử giá trị với $x = \frac{3 π}{2}$ thì y=-1 thấy hàm số $\cos \frac{2 x}{3}$ thỏa mãn.

Chọn đáp án A.

Câu 18:

Tập nghiệm của phương trình sin(πx) = cos(π/3+πx) là

A. {π/12+kπ,k∈Z}

B. {1/12+k,k∈Z}

C. {π/2+kπ,k∈Z}

D. {1/2+kπ,k∈Z}

Xem đáp án

Chọn B

$\sin (π x) = \cos (\frac{π}{3} + π x)$
$\Leftrightarrow \cos (\frac{π}{2} - π x) = \cos (\frac{π}{3} + π x)$ hay $\cos (\frac{π}{3} + π x) = \cos (\frac{π}{2} - π x)$
$\Leftrightarrow [\begin{array}{l} \frac{π}{3} + π x = \frac{π}{2} - π x + k 2 π \\ \frac{π}{3} + π x = - \frac{π}{2} + π x + k 2 π (l) \end{array}$
$\Leftrightarrow 2 π x = \frac{π}{6} + k 2 π$

$\Leftrightarrow x = \frac{1}{12} + k$

Câu 19:

Nghiệm của phương trình $\sin^{2} x + \sin x \cos x = 1$ là:

A. $x = - \frac{π}{4} + k π hoặc x = \frac{π}{2} + kπ, k \in ℤ$

B. $x = \frac{π}{4} + k π hoặc x = \frac{π}{2} + kπ, k \in ℤ$

C. $x = - \frac{π}{4} + k 2 π hoặc x = \frac{π}{2} + k 2 π, k \in ℤ$

D. $x = \frac{π}{4} + k 2 π hoặc x = \frac{π}{2} + k 2 π, k \in ℤ$

Xem đáp án

Đáp án đúng là B.

Giải thích

$\sin^{2} x + \sin x \cos x = 1$
$\Leftrightarrow 1 - \sin^{2} x - \sin x \cos x = 0$
$\Leftrightarrow \cos^{2} x - \sin x \cos x = 0$
$\Leftrightarrow \cos x (\cos x - \sin x) = 0$
$\Leftrightarrow [\begin{array}{l} \cos x = 0 \Rightarrow x = \frac{π}{2} + k π \\ \cos x = \sin x, (*) \end{array}$

Giải (*)

$(*) \Leftrightarrow \cos x = \cos (\frac{π}{2} - x)$
$\Leftrightarrow [\begin{array}{l} x = \frac{π}{2} - x + k 2 π \\ x = \frac{- π}{2} + x + k 2 π \end{array}$

$\Leftrightarrow x = \frac{π}{4} + k π$

Câu 20:

Tập nghiệm của phương trình $\cos^{3} x + \sin^{3} x = \sin x + \cos x$ là:

A. $\{- \frac{π}{4} + k π, k \frac{π}{2}; k \in ℤ\}$

B. $\{- \frac{π}{4} + k 2 π, kπ; k \in ℤ\}$

C. $\{- \frac{π}{4} + k π; k \in ℤ\}$

D. $\{k \frac{π}{2}; k \in ℤ\}$

Xem đáp án

Chọn A

$\cos^{3} x + \sin^{3} x = \sin x + \cos x$
$\Leftrightarrow (\cos x + \sin x) (\cos^{2} x - \cos x . \sin x + \sin^{2} x) - (\sin x + \cos x) = 0$
$\Leftrightarrow (\cos x + \sin x) (1 - \cos x . \sin x) - (\sin x + \cos x) = 0$
$\Leftrightarrow (\sin x + \cos x) (1 - \cos x . \sin x - 1) = 0$
$\Leftrightarrow (\sin x + \cos x) (- \cos x . \sin x) = 0$
$\Leftrightarrow [\begin{array}{l} \sin x + \cos x = 0 \\ - \cos x . \sin x = 0 \end{array}$
$\Leftrightarrow [\begin{array}{l} \sin x . \frac{1}{\sqrt{2}} + \cos x . \frac{1}{\sqrt{2}} = 0 \\ \sin 2 x = 0 \end{array}$
$\Leftrightarrow [\begin{array}{l} \sin (\frac{π}{4} + x) = 0 \\ \sin 2 x = 0 \end{array}$
$\Leftrightarrow [\begin{array}{l} \frac{π}{4} + x = k π \\ 2 x = k π \end{array}$
$\Leftrightarrow [\begin{array}{l} x = - \frac{π}{4} + k π \\ x = \frac{k π}{2} \end{array}$

Câu 21:

Trong các phương trình sau phương trình nào vô nghiệm?

A. 3sinx + 1 = 0

B. $2 \cos^{2} x - \cos x - 1 = 0$

C. 5tanx + 3 = 0

D. 3cosx – 5 = 0

Xem đáp án

Chọn D

$3 \cos x - 5 = 0$

$\Leftrightarrow \cos x = \frac{5}{3} > 1$ (vô lí vì $- 1 \leq \cos x \leq 1$ )

Vậy phương trình vô nghiệm

Câu 22:

Tập xác định của hàm số $y = \sin \sqrt{x}$ là:

A. R

B. R\{0}

C. [0;+∞)

D. (0;- ∞)

Xem đáp án

ĐKXĐ.: $x \geq 0$

TXĐ: $D = [0; + \infty)$

Chọn đáp án C.

Câu 23:

Tập nghiệm của phương trình $3 \sin 3 x - \sqrt{3} \cos 9 x = 1 + 4 \sin^{3} 3 x$ là:

A. $\{\frac{π}{18} + k \frac{2 π}{9}, \frac{7 π}{54} + k \frac{2 π}{9}, k \in ℤ\}$

B. $\{\frac{π}{18}; \frac{7 π}{54}\}$

C. $\{\frac{π}{18} + k \frac{2 π}{9}, \frac{- π}{54} + k \frac{2 π}{9}, k \in ℤ\}$

D. $\emptyset$

Xem đáp án

Chọn A

Câu 24:

Tập nghiệm của phương trình $c o t 2 x + 2 \sin 2 x = 1 / \sin 2 x$ là:

A. $\{\pm \frac{π}{6} + k π, kπ; k \in ℤ\}$

B. $\{\pm \frac{π}{3} + k π; k \in ℤ\}$

C. $\{\pm \frac{π}{3} + k π, kπ; k \in ℤ\}$

D. $\{\pm \frac{π}{6} + k π; k \in ℤ\}$

Xem đáp án

Chọn B

* Với cos 2x = 1 thì sin2x =0 ( không thỏa mãn điều kiện)

Câu 25:

Phương trình $2 \sin^{2} x - 5 \sin x \cos x - \cos^{2} x + 2 = 0$ có cùng tập nghiệm với phương trình nào trong số bốn phương trình sau:

A. $4 \sin^{2} x - 5 \sin x \cos x - \cos^{2} x = 0$

B. $4 \sin^{2} x + 5 \sin x \cos x + \cos^{2} x = 0$

C. $4 \tan^{2} x - 5 \tan x + 1 = 0$

D. $5 \sin 2 x + 3 \cos 2 x = 2$

Xem đáp án

Chọn C

Ta có:

$\begin{array}{l} 2 \sin^{2} x - 5 \sin x . c {osx -cos}^{2} x + 2 = 0 \\ \Leftrightarrow 2 \sin^{2} x - 5 \sin x . c {osx -cos}^{2} x + 2 (\sin^{2} x + c {os}^{2} x) = 0 \\ \Leftrightarrow 4 \sin^{2} x - 5 \sin x . c {osx + cos}^{2} x = 0 (*) \end{array}$