Trắc nghiệm Toán 11 Bài 5: Xác suất của biến cố (phần 1) (có đáp án)
-
1385 lượt thi
-
28 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Lấy ngẫu nhiên 1 thẻ từ 1 hộp 30 thẻ được đánh số từ 1 đến 30.
Tính xác suất để thẻ được lấy ghi số 6
 Xem đáp án
Xem đáp án
Không gian mẫu Ω={1,2,..30}. kí hiệu A là biến cố “ thẻ lấy ra ghi số 6”,
A={6}, n(A) =1,n(Ω) = 30
⇒P(A) =1/30
Chọn đáp án A
Câu 2:
Lấy ngẫu nhiên 1 thẻ từ 1 hộp 30 thẻ được đánh số từ 1 đến 30.
Tính xác suất để thẻ được lấy ghi số chia hết cho 5
 Xem đáp án
Xem đáp án
Gọi B là biến cố "lấy được thẻ chia hết cho 5".
B = {5,10,15,20,25,30}, n(B) = 6
⇒P(B) =6/30 =1/5
Chọn đáp án là B
Nhận xét: học sinh có thể nhầm với số thẻ và số ghi trên thẻ, hoặc vận dụng nhầm công thức P(A) =(n(Ω))/(n(A)) dẫn đến các phương án khác còn lại.
Câu 3:
Một lớp học có 40 học sinh trong đó có 15 học sinh giỏi Toán, 10 học sinh giỏi Văn và 5 học sinh giỏi cả Văn và Toán. Chọn ngẫu nhiên một học sinh.
Xác suất của biến cố A:”học sinh được chọn giỏi Toán” là:
 Xem đáp án
Xem đáp án
Ta có n(Ω) = 40
Vì có 15 học sinh giỏi toán nên: n(A) = 15
Suy ra: P(A) = 15/40 = 3/8
Chọn đáp án là C
Câu 4:
Một lớp học có 40 học sinh trong đó có 15 học sinh giỏi Toán, 10 học sinh giỏi Văn và 5 học sinh giỏi cả Văn và Toán. Chọn ngẫu nhiên một học sinh.
Xác suất của biến cố B:”học sinh được chọn giỏi Văn” là:
 Xem đáp án
Xem đáp án
Ta có n(Ω) = 40
Vì có 10 học sinh giỏi văn nên n(B) = 10
Suy ra, P(B) = 10/40 =1/4
Chọn đáp án B
Câu 5:
Một lớp học có 40 học sinh trong đó coa 15 học sinh giỏi Toán, 10 học sinh giỏi Văn và 5 học sinh giỏi cả Văn và Toán. Chọn ngẫu nhiên một học sinh.
Xác suất của biến cố C:”học sinh được chọn không giỏi Văn và Toán” là:
 Xem đáp án
Xem đáp án
Chọn đáp án C
Ta có n(Ω) = 40
Số học sinh giỏi Văn hoặc Toán gồm: học sinh chỉ giỏi Văn, học sinh chỉ giỏi Toán, học sinh giỏi cả Văn và Toán nên bằng
(15 +10) -5 = 20 em.
Do đó, số học sinh không giỏi cả Toán và Văn là 40 – 20 = 20 em, nên n(C) = 20
Vì vậy P(C) =(n(C))/(n(Ω))=1/2
Câu 6:
Lớp 11B có 25 đoàn viên trong đó có 10 nam và 15 nữ. Cho ngẫu nhiên 3 đoàn viên trong lớp để tham dự hội trại ngày 26 tháng 3. Tính xác suất để 3 đoàn viên được chọn có 2 nam và 1 nữ.
 Xem đáp án
Xem đáp án
Chọn 3 đoàn viên trong 25 đoàn viên thì có C253 cách chọn, do đó ta có: n(Ω) = C253 = 2300 phần tử
Có 10 đoàn viên nam chọn 2 đoàn viên thì có C102 cách chọn; có 15 đoàn viên nữ chọn 1 nữ thì có C151 cách chọn.
Gọi A là biến cố:”3 đoàn viên được chọn có 2 nam và 1 nữ” thì số phần tử của tập A là n(A) =C102.C151=675
Vậy P(A) =(n(A))/(n(Ω))=675/2300=27/92. Chọn đáp án B
Nhận xét: học sinh thường mắc một số sai lầm khi tính:
n(A) =C102+C151=60 ⇒P(A)=3/115
n(A) = A102.A151=1350;n(Ω)=A253=13800 ⇒ P(A)=9/92
n(A) = A102+A151=105;n(Ω)=A253=13800 ⇒P(A)=7/920
Chọn D
Câu 7:
Hai xạ thủ cùng bắn mỗi người một viên đạn vào bia một cách độc lập với nhau. Xác suất bắn trúng bia của hai xạ thủ lần lượt là 1/2 và 1/3
Tính xác suất của biến cố X:”cả hai xạ thủ đều bắn trúng bia”
 Xem đáp án
Xem đáp án
Gọi A là biến cố “Xạ thủ thứ i bắn trúng bia” i = 1,2.
Khi đó, P(A1) =1/2; P(A2) = 1/3;
Hai biến cố A1 và A2 độc lập với nhau
X =A1∩ A2 nên P(X) = P(A1∩ A2) = P(A1.A2) = P(A1).P(A2) = 1/6
Chọn đáp án là B
Câu 8:
Hai xạ thủ cùng bắn mỗi người một viên đạn vào bia một cách độc lập với nhau. Xác suất bắn trúng bia của hai xạ thủ lần lượt là 1/2 và 1/3
Tính xác suất của biến cố Y:”có ít nhất một xạ thủ không bắn trúng bia”
 Xem đáp án
Xem đáp án
Gọi A là biến cố “Xạ thủ thứ i bắn trúng bia”, i=1,2
TH1. Xạ thủ thứ nhất bắn trúng, xạ thủ 2 bắn trượt thì xác suất là:
TH2. Xạ thủ thứ nhất bắn trượt, xạ thủ thứ 2 bắn trúng thì xác suất là:
TH3. Cả 2 xạ thủ đều bắn trượt
Xác suất của biến cố Y là:
Đáp án. D
Câu 9:
Một cái túi chứa 3 viên bi đỏ và 5 bi xanh, 6 viên bi vàng. Chọn ngẫu nhiên 3 viên bi.
Số kết quả có thể xảy ra là:
 Xem đáp án
Xem đáp án
Số các kết quả có thể xảy ra là = 364
Chọn D
Câu 10:
Một cái túi chứa 3 viên bi đỏ và 5 bi xanh, 6 viên bi vàng. Chọn ngẫu nhiên 3 viên bi.
Xác suất để 3 viên bi có cả ba màu đỏ, xanh, vàng là
 Xem đáp án
Xem đáp án
Số phần tử của không gian mẫu là:
Gọi A là biến cố:” lấy được 3 bi có đủ 3 màu đỏ, xanh, vàng” thì
![]()
Chọn B
Câu 11:
Gieo 3 con súc sắc cân đối, đồng chất. Khi đó, số kết quả có thể xảy ra là:
 Xem đáp án
Xem đáp án
Mỗi con xúc sắc có 6 khả năng xảy ra.
Vì vậy số kết quả có thể xảy ra là 6. 6.6= 216
Chọn C
Câu 12:
Gieo 3 con súc sắc cân đối, đồng chất và quan sát số chấm xuất hiện. Khi đó: Xác suất để tổng số chấm xuất hiện trên mặt ba con súc sắc bằng 12 là:
 Xem đáp án
Xem đáp án
Gọi B là biến cố: “Tổng số chấm xuất hiện trên bề mặt 3 con súc sắc bằng 12”
Ta thấy
Nếu số chấm trên bề mặt 3 con súc sắc khác nhau tức là các trường hợp (1;5;6), (2;4;6), (3;4;5) có cách
Nếu số chấm trên bề mặt 3 con súc sắc có 2 con giống nhau tức là các trường hợp (2;5;5) và (3;3;6) có cách
Nếu số chấm trên bề mặt 3 con súc sắc giống nhau ta có 1 cách gieo duy nhất
. Vậy .
Chọn A
Câu 13:
Chọn ngẫu nhiên 5 sản phẩm trong 10 sản phẩm. Biết rằng trong 10 sản phẩm đó có 2 phế phẩm.
Tính xác suất để trong 5 sản phẩm được chọn đó không có phế phẩm nào
 Xem đáp án
Xem đáp án
Số cách chọn 5 sản phẩm trong 10 sản phẩm là n(Ω) = =252
Trong 10 sản phẩm đó có 2 phế phẩm nên có 8 sản phẩm tốt.
Gọi A là biến cố:” trong 5 sản phẩm được chọn không có phế phẩm nào”.
n(A)= =56 → P(A)= 56/252=2/9
Chọn C
Câu 14:
Chọn ngẫu nhiên 5 sản phẩm trong 10 sản phẩm. Biết rằng trong 10 sản phẩm đó có 2 phế phẩm.
Tính xác suất để trong 5 sản phẩm được chọn có ít nhất 1 phế phẩm
 Xem đáp án
Xem đáp án
Số khả năng chọn 5 sản phẩm trong 10 sản phẩm là n(Ω) =C105=252
Vì trong 10 sản phẩm có 2 phế phẩm nên có 8 sản phẩm tốt
Gọi B là biến cố:” trong 5 sản phẩm được chọn có ít nhất 1 phế phẩm” thì :
Biến cố đối : Trong 5 sản phẩm lấy ra không có phế phẩm.
Số kết quả thuận lợi cho biến cố
Chọn C
Câu 15:
Chọn ngẫu nhiên 5 sản phẩm trong 10 sản phẩm. Biết rằng trong 10 sản phẩm đó có 2 phế phẩm.
Tính xác suất để trong 5 sản phẩm được chọn có đúng 1 phế phẩm
 Xem đáp án
Xem đáp án
Số khả năng chọn 5 sản phẩm trong 10 sản phẩm là n(Ω) =C105=252
Trong 10 sản phẩm, có 2 phế phẩm nên có 8 sản phẩm tốt.
Gọi C là biến cố:” trong 5 sản phẩm được chọn có đúng một phế phẩm”.
Khi đó, lấy được 4 sản phẩm tốt và 1 phế phẩm.
n(C)= → P( C) =140/252=5/9
Chọn B
Câu 16:
Trong một buổi liên hoan có 6 cặp nam nữ, trong đó có 3 cặp là vợ chồng. Chọn ngẫu nhiên 3 người trong số đó tham gia trò chơi.
Tính xác suất để trong 3 người được chọn có đúng 1 người là nam
 Xem đáp án
Xem đáp án
Số khả năng chọn ngẫu nhiên 3 người từ 6.2= 12 người là = 220
Gọi A là biến cố:” trong 3 người được chọn có đúng 1 nam”. Khi đó, 2 người còn lại là nữ.
n(A)= = 90. Do đó P(A) =90/220=9/22
Chọn B
Câu 17:
Trong một buổi liên hoan có 6 cặp nam nữ, trong đó có 3 cặp là vợ chồng. Chọn ngẫu nhiên 3 người trong số đó tham gia trò chơi. Tính xác suất để trong 3 người được chọn không có cặp vợ chồng nào
 Xem đáp án
Xem đáp án
Số khả năng chọn ngẫu nhiên 3 người từ 6.2= 12 người là = 220
Gọi B là biến cố :” trong 3 người được chọn không có cặp vợ chồng nào” thì là biến cố :” có đúng một cặp vợ chồng trong ba người được chọn”
![]()
( vì có 3 cách chọn cặp vợ chồng, và 10 cách chọn người thứ 3 trong số 10 người còn lại) nên
![]()
Chọn D
Câu 18:
Trong một bài thi trắc nghiệm khách quan có 20 câu, mỗi câu có 4 phương án trả lời trong đó chỉ có 1 phương án đúng. Một học sinh không học bài nên làm bài bài bằng cách chọn ngẫu nhiên mỗi câu một phương án. Tính xác suất để học sinh đó trả lời đúng 10 câu?
 Xem đáp án
Xem đáp án
Gọi Ai là biến cố:” học sinh chọn đúng ở câu i” i= 1,2,..,20
Ta có :
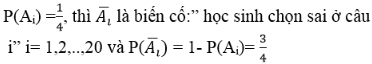
Gọi X là biến cố:” Học sinh trả lời đúng 10 câu trong 20 câu”
Số cách chọn 10 câu đúng trong 20 câu là
Chọn D
Câu 19:
Có hai hộp bút chì. Hộp 1 có 3 bút đỏ và 4 bút xanh. Hộp II có 8 bút đỏ và 4 bút xanh. Chọn ngẫu nhiên từ mỗi hộp ra 1 bút. Tính xác suất để có 1 bút đỏ và 1 bút xanh.
 Xem đáp án
Xem đáp án
Gọi A là biến cố: “chọn bút đỏ ở hộp thứ i"
Gọi B là biến cố: “chọn bút xanh ở hộp thứ i", với i=1,2
Ta có
Gọi X là biến cố: “chọn được 1 bút đỏ và 1 bút xanh” thì
.
Chọn C.
Câu 20:
Một chiếc máy có ba động cơ I,II,III hoạt động độc lập với nhau. Xác xuất để động cơ I,II,III chạy tốt tương ứng là 0,7; 0,8; 0,9.
Xác suất để cả 3 động cơ chạy tốt là
 Xem đáp án
Xem đáp án
Gọi Ai là biến cố:” động cơ i chạy tốt” i=1,2,3
P(A1)= 0,7 ; P(A2).= 0,8 ; P(A3)=0,9 và A1, A2, A3 độc lập với nhau
Khi đó, A1. A2. A3 là biến cố:” cả 3 biến cố đều chạy tốt ”
P(A1. A2. A3)= P(A1). P(A2). P(A3)= 0,504
Chọn C
Câu 21:
Một chiếc máy có ba động cơ I,II,III hoạt động độc lập với nhau. Xác xuất để động cơ I,II,III chạy tốt tương ứng là 0,7; 0,8; 0,9.
Xác suất để cả ba động cơ chạy không tốt
 Xem đáp án
Xem đáp án
Gọi Ai là biến cố:” động cơ i chạy tốt” i=1,2,3
P(A1)= 0,7 ; P(A2).= 0,8 ; P(A3)=0,9 và A1, A2, A3 độc lập với nhau
. Ba biến cố này độc lập với nhau
![]()
Chọn A
Câu 22:
Một chiếc máy có ba động cơ I,II,III hoạt động độc lập với nhau. Xác xuất để động cơ I,II,III chạy tốt tương ứng là 0,7;0,8;0,9.
Xác suất để có ít nhất 1 động cơ chạy tốt là
 Xem đáp án
Xem đáp án
Gọi Ai là biến cố:” động cơ i chạy tốt” i=1,2,3
P(A1)= 0,7 ; P(A2).= 0,8 ; P(A3)=0,9 và A1, A2, A3 độc lập với nhau
và ba biến cố này độc lập với nhau
Gọi X là biến cố :” có ít nhất một động cơ chạy tốt” thì X là biến cố đối của :
![]()
Chọn D
Câu 23:
Một bộ bài tú lơ khơ gồm 52 con, lấy ngẫu nhiên lần lượt có hoàn lại từng con cho đến khi lần đầu tiên lấy được con át thì dừng. Tính xác suất sao cho quá trình dừng lại ở ngay lần thứ nhất
 Xem đáp án
Xem đáp án
Một bộ bài có 52 cây, trong đó có 4 con át.
Kí hiệu Ak: “ lần thứ k lấy được con át” k≥1 thì P(A1)=4/52=1/13
Ta tính P(A1)= 1/13
Chọn B
Câu 24:
Một bộ bài tú lơ khơ gồm 52 con, lấy ngẫu nhiên lần lượt có hoàn lại từng con cho đến khi lần đầu tiên lấy được con át thì dừng. Tính xác suất sao cho quá trình dừng lại ở lần thứ 3
 Xem đáp án
Xem đáp án
Bộ bài có 52 cây tú, trong đó có 4 cây át.
Kí hiệu Ak: “ lần thứ k lấy được con át” k≥1 thì
Để quá trình dừng lại ở lần thứ 3 thì 2 lần đầu tiên lấy được cây khác át, lần thứ 3 lấy được cây át.
Ta cần tính :
Chọn C
Câu 25:
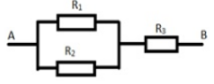
Một mạch điện gồm 3 link kiện như hình vẽ, trong đó xác suất hỏng của từng linh kiện 1,2,3 trong khoảng thời gian t nào đó tương ứng là 0,2; 0,1 và 0,05. Biết rằng các linh kiện làm việc độc lập với nhau và các dây luôn tốt. Tính xác suất để mạch hoạt động được trong thời gian t nào đó.
 Xem đáp án
Xem đáp án
Xác suất để linh kiện 1 hoạt động tốt là: 1-0,2=0,8
Xác suất để linh kiện 2 hoạt động tốt là: 1-0,1=0,9
Xác suất để linh kiện 3 hoạt động tốt là: 1-0,05=0,95
Lưu ý rằng khi mắc mạch song song, linh kiện 1 hỏng thì linh kiện 2 vẫn hoạt động tốt và ngược lại.
Xác suất để cả 3 linh kiện hoạt động tốt là:
Xác suất để linh kiện 1 hỏng, 2 linh kiện còn lại hoạt động tốt là:
Xác suất để linh kiện 2 hỏng, 2 linh kiện còn lại hoạt động tốt là:
Vậy xác suất để mạch hoạt động được là:
Chọn đáp án A.
Câu 26:
Số cách xếp 6 bạn A,B,C,D,E,F ngồi vào bàn học gồm 6 chỗ là:
 Xem đáp án
Xem đáp án
Chọn C
Số cách xếp 6 bạn vào 6 chỗ ngồi là hoán vị của 6. Nên có 6!=720 cách xếp
Câu 27:
Số cách xếp 5 bạn A,B,C,D,E ngồi vào bàn tròn 5 chỗ là:
 Xem đáp án
Xem đáp án
Chọn C
Vì xếp bàn tròn nên ta cố định chỗ ngồi cho 1 bạn. Còn 4 bạn nữa phải xếp chỗ là hoán vị của 4. Nên có 1.4!=24 cách xếp.
Câu 28:
Có bao nhiêu số tự nhiên có 4 chữ số khác nhau đôi một?
 Xem đáp án
Xem đáp án
Chọn C
Gọi số có 4 chữ số khác nhau là
Có 9 cách chọn a,với mỗi cách chọn a có :
![]()
Vậy có tất cả 9. A93= 4536 số
