299 câu trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết(P7)
-
2781 lượt thi
-
40 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Một tổ học sinh có 7 nam và 3 nữ. Chọn ngẫu nhiên 2 người. Tính xác suất sao cho 2 người được chọn đều là nữ
 Xem đáp án
Xem đáp án
Chọn A
Số phần tử của không gian mẫu ![]() .
.
Gọi A là biến cố 2 người được chọn đều là nữ, suy ra ![]() .
.
Xác suất để 2 người được chọn đều là nữ là: 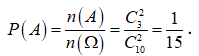
Câu 2:
Có hai hộp chứa các quả cầu. Hộp thứ nhất chứa 7 quả cầu đỏ và 5 quả cầu màu xanh, hộp thứ hai chứa 6 quả cầu đỏ và 4 quả cầu màu xanh. Lấy ngẫu nhiên từ một hộp 1 quả cầu. Xác suất sao cho hai quả lấy ra cùng màu đỏ.
 Xem đáp án
Xem đáp án
Chọn A
Gọi T là phép thử lấy mỗi hộp ra một quả. Số phần tử của không gian mẫu trong phép thử T là![]()
Gọi A là biến cố hai quả lấy ra từ mỗi hộp đều là màu đỏ. Số phần tử của biến cố A là: ![]() .
.
Vậy xác suất của biến cốA là 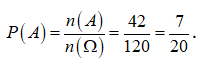 .
.
Câu 3:
Một tổ học sinh có 7 nữ và 4 nam. Chọn ngẫu nhiên 2 người đi trực cờ đỏ. Tính xác suất sao cho 2 người được chọn đều là nam.
 Xem đáp án
Xem đáp án
Chọn C
Số phần tử của không gian mẫu là: ![]() .
.
Gọi biến cố A: “ Hai người được chọn đều là nam”.
![]()
Vậy xác suất cần tìm là: 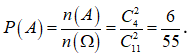 .
.
Câu 4:
Đội văn nghệ của một lớp có 5 bạn nam và 7 bạn nữ. Chọn ngẫu nhiên 5 bạn tham gia biểu diễn, xác suất để trong 5bạn được chọn có cả nam và nữ, đồng thời số nam nhiều hơn số nữ bằng
 Xem đáp án
Xem đáp án
Chọn B.
Không gian mẫu có số phần tử là ![]() .
.
Gọi A là biến cố: “Trong 5 bạn được chọn có cả nam và nữ, đồng thời số nam nhiều hơn số nữ”. Khi đó, số kết quả thuận lợi cho biến cố A là: ![]() .
.
Vậy xác suất cần tính là 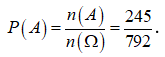 .
.
Câu 5:
Một người muốn gọi điện thoại nhưng nhớ được các chữ số đầu mà quên mất ba chữ số cuối của số cần gọi. Người đó chỉ nhớ rằng ba chữ số cuối đó phân biệt và có tổng bằng 5. Tính xác suất để người đó bấm máy một lần đúng số cần gọi.
 Xem đáp án
Xem đáp án
Chọn C
Có 2 bộ số {a;b;c} có tổng các chữ số bằng 5 là: {0;1;4}, {0;2;3}, mỗi bộ số có 3! hoán vị nên có tất cả 12 khả năng.
Do đó xác suất để người đó bấm máy một lần đúng số cần gọi là .
Câu 6:
Một người đang đứng tại gốc O của trục tọa độ Oxy. Do say rượu nên người này bước ngẫu nhiên sang trái hoặc sang phải trên trục tọa độ với độ dài mỗi bước bằng 1 đơn vị. Xác suất để sau 10 bước người này quay lại đúng gốc tọa độ O bằng
 Xem đáp án
Xem đáp án
Chọn C
Mỗi bước người này có 2 lựa chọn sang trái hoặc phải nên số phần tử không gian mẫu là .
Để sau đúng 10 bước người này quay lại đúng gốc tọa độ O thì người này phải sang trái 5 lần và sang phải 5 lần, do đó số cách bước trong 10 bước này là .
Xác suất cần tính bằng ![]() .
.
Câu 7:
Có 8 học sinh nam, 5 học sinh nữ và 1 thầy giáo được sắp xếp ngẫu nhiên đứng thành một vòng tròn. Tính xác suất để thầy giáo đứng giữa 2 học sinh nam.
 Xem đáp án
Xem đáp án
Chọn B
Số phần tử của không gian mẫu là: 13!
Gọi A là biến cố: “Thầy giáo đứng giữa 2 học sinh nam”
Bước 1: Xếp hai học sinh nam đứng cạnh thầy giáo có .
Coi hai học sinh nam đứng cạnh thầy giáo và thầy giáo là một người.
Bước 2: Xếp 12 người quanh một bàn tròn có 11! cách.
Số kết quả thuận lợi của biến cố A là: .11!
Vậy 
Câu 8:
Gieo đồng thời hai con súc sắc cân đối và đồng chất.Tính xác suất P để hiệu số chấm trên các mặt xuất hiện của hai con súc sắc bằng 2.
 Xem đáp án
Xem đáp án
Chọn B
Số phần tử của không gian mẫu: ![]()
Gọi A là biến cố thỏa mãn yêu cầu bài toán:
![]()
![]() nên n(A) = 8
nên n(A) = 8
Vậy ![]()
Câu 9:
Kết quả (b,c) của việc gieo một con súc sắc cần đối hai lần liên tiếp, trong đó b là số chấm xuất hiện trong lần gieo thứ nhất, c là số chấm xuất hiện trong lần gieo thứ hai được thay vào phương trình bậc hai + bx + c = 0 (x). Tính xác suất để phương trình bậc hai đó có nghiệm.
 Xem đáp án
Xem đáp án
Chọn C
Số phần tử của không gian mẫu của phép thử gieo một con súc sắc hai lần liên tiếp là 36.
Để phương trình bậc hai + bx + c = 0 có nghiệm là ![]() (*) với
(*) với ![]()
Gọi A là biến cố chọn cặp số (b;c) thỏa mãn ![]() trong đó
trong đó ![]()
Khi c = 1: Các giá trị của b thỏa mãn điều kiện (*) là: 2,3,4,5,6. Suy ra có: 5 cặp (b,c).
Khi c = 2: Các giá trị của b thỏa mãn điều kiện (*) là: 3,4,5,6. Suy ra có: 4 cặp (b,c).
Khi c = 3: Các giá trị của b thỏa mãn điều kiện (*) là: 4,5,6. Suy ra có: 3 cặp (b,c).
Khi c = 4: Các giá trị của b thỏa mãn điều kiện (*) là: 4,5,6. Suy ra có: 3 cặp (b,c).
Khi c = 5: Các giá trị của b thỏa mãn điều kiện (*) là: 5,6. Suy ra có: 2 cặp (b,c).
Khi c = 6: Các giá trị của b thỏa mãn điều kiện (*) là: 5,6. Suy ra có: 2 cặp (b,c).
Vậy, số cặp (b,c) thỏa mãn điều kiện (*) là 19
Câu 10:
Một đề kiểm tra Toán Đại số và Giải tích chương 2 của khối 11 có 20 câu trắc nghiệm. Mỗi câu có 4 phương án lựa chọn, trong đó chỉ có 1 đáp án đúng. Mỗi câu trả lời đúng được 0,5 điểm và mỗi câu trả lời sai không được điểm nào. Một học sinh không học bài nên tích ngẫu nhiên câu trả lời. Tính xác suất để học sinh nhận được 6 điểm (kết quả làm tròn đến 4 chữ số sau dấu phẩy thập phân).
 Xem đáp án
Xem đáp án
Chọn D
Gọi A là biến cố “Học sinh nhận được 6 điểm”.
Xác suất đánh đúng 1 câu là và đánh sai 1 câu là .
Để nhận được 6 điểm học sinh đó cần đánh đúng 12 câu và sai 8 câu.
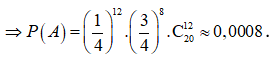
Câu 11:
Một hộp đựng 15 quả cầu trong đó có 6 quả màu đỏ, 5 quả màu xanh, 4 quả màu vàng. Lấy ngẫu nhiên 6 quả cầu trong 15 quả cầu đó. Tính xác suất để 6 quả lấy được có đủ ba màu.
 Xem đáp án
Xem đáp án
Chọn D
Gọi là không gian mẫu, ta có n() = = 5005.
Gọi A là biến cố: “6 quả lấy được có đủ ba màu”
: “6 quả lấy được không có đủ ba màu”.
TH1: 6 quả lấy được chỉ một màu đỏ có = 1cách.
TH2: 6 quả lấy được có hai màu
+ 6 quả lấy được có hai màu đỏ và xanh: có ![]() cách.
cách.
+ 6 quả lấy được có hai màu đỏ và vàng: có ![]() cách.
cách.
+ 6 quả lấy được có hai màu đỏ và xanh: có ![]() cách.
cách.
![]()

Vậy 
Câu 12:
Chọn ngẫu nhiên một số tự nhiên nhỏ hơn 300. Gọi A là biến cố “số được chọn không chia hết cho 3”. Tính xác suất P(A) của biến cố A.
 Xem đáp án
Xem đáp án
Chọn A
Có 300 số tự nhiên nhỏ hơn 300 nên n() = 300.
Số các số tự nhiên nhỏ hơn 300 mà chia hết cho 3 là: (297-0):3 + 1 = 100.
Số các số tự nhiên nhỏ hơn 300 mà không chia hết cho 3 là: 300 - 100 = 200 nên n(A) = 200.
Vậy 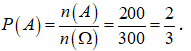
Câu 13:
Trong một hộp có 3 bi đỏ, 5 bi xanh và 7 bi vàng. Bốc ngẫu nhiên 4 viên. Xác suất để bốc được đủ 3 màu là
 Xem đáp án
Xem đáp án
Chọn B
Hộp có 3 + 5 + 7 = 15 viên bi.
Số phần tử của không gian mẫu là: ![]() .
.
TH1: Bốc được 4 viên trong đó có 2 viên bi đỏ, 1 viên bi trắng và 1 viên bi vàng.
![]()
TH2: Bốc được 4 viên trong đó có 1 viên bi đỏ, 2 viên bi trắng và 1 viên bi vàng.
![]()
TH3: Bốc được 4 viên trong đó có 1 viên bi đỏ, 1 viên bi trắng và 2 viên bi vàng.
![]()
Vậy số cách bốc 4 viên có đủ 3 màu là 105 + 310 + 315 = 630 cách.
Vậy xác suất cần tìm là: ![]()
Câu 14:
Gọi S là tập hợp tất cả các số tự nhiên có 4 chữ số được lập từ tập hợp X = {1;2;3;4;5;6;7;8;9}. Chọn ngẫu nhiên một số từ S. Tính xác suất chọn được số chia hết cho 6
 Xem đáp án
Xem đáp án
Chọn A
+ Ta có ![]()
![]()
Ta có d có 4 cách chọn {2;4;6;8}, a có 9 cách chọn, b có 9 cách chọn. Vì a + b + d khi chia cho 3 có 3 khả năng số dư
{0;1;2}, mà ![]() nên c có 3 cách chọn.
nên c có 3 cách chọn.
Ta có: ![]()
Xác suất cần tìm là: 
Câu 15:
Từ một hộp chứa 11 quả cầu màu đỏ và 4 quả cầu màu xanh, lấy ngẫu nhiên đồng thời 3 quả cầu. Xác suất để lấy được 3 quả cầu màu xanh bằng
 Xem đáp án
Xem đáp án
Chọn A
Ta có ![]()
Gọi A là biến cố “lấy được 3 quả cầu màu xanh”.![]()
Nên 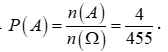
Câu 16:
Trên giá sách có 4 quyển sách toán, 5 quyển sách lý. Lấy ngẫu nhiên ra 3 quyển sách. Tính xác suất để 3 quyển được lấy ra có ít nhất một quyển toán.
 Xem đáp án
Xem đáp án
Chọn D.
Lấy ngẫu nhiên 3 quyển sách có: ![]() cách.
cách.
Gọi A là biến cố: 3 quyển được lấy ra có ít nhất một quyển toán.
Suy ra là biến cố: lấy 3 quyển sách và không có quyển nào là quyển toán.
Khi đó ![]()
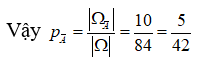
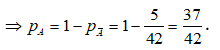
Câu 17:
Trong hệ trục tọa độ Oxy cho A(-2;0), B(-2;2), C(4;2), D(4;0). Chọn ngẫu nhiên một điểm có tọa độ (x;y) (với x, y ) nằm trong hình chữ nhật ABCD (kể cả các điểm trên cạnh). Gọi A là biến cố: “x, y đều chia hết cho 2”. Xác suất của biến cố A là .
 Xem đáp án
Xem đáp án
Chọn B
Ta có ![]()
Do đó ![]()
Ta cũng có ![]() => n(A) = 8
=> n(A) = 8
Vậy xác suất của biến cố A là P(A) =
Câu 18:
Một chiếc hộp chứa 6 quả cầu màu xanh và 4 quả cầu màu đỏ. Lấy ngẫu nhiên từ chiếc hộp ra 5 quả cầu. Tính xác suất để trong 5 quả cầu lấy được có đúng 2 quả cầu màu đỏ.
 Xem đáp án
Xem đáp án
Chọn B
Chiếc hộp chứa 6 quả cầu màu xanh và 4 quả cầu màu đỏ. Lấy ngẫu nhiên từ chiếc hộp ra 5 quả cầu nên số phần tử của không gian mẫu là ![]()
Gọi A là biến cố: ”5 quả cầu lấy được có đúng 2 quả cầu màu đỏ”.
Lấy 2 quả cầu màu đỏ và 3 quả cầu màu xanh nên số phần tử của biến cố A là:
![]()
Xác suất cần tìm là:
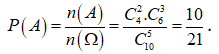
Câu 19:
Tổ toán của một trường THPT có 4 thầy giáo và 10 cô giáo. Tổ chọn ngẫu nhiên 2 giáo viên để đi tập huấn. Tính xác suất để 2 giáo viên được chọn gồm 1 thầy giáo và 1 cô giáo.
 Xem đáp án
Xem đáp án
Chọn C
Gọi biến cố A: “2 giáo viên tập huấn gồm 1 thầy giáo và 1 cô giáo”.
Suy ra ![]() .
.
Vậy 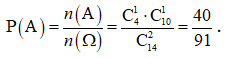 .
.
Câu 20:
Cho tập hợp S = {1,2,3...,17} gồm 17 số nguyên dương đầu tiên. Chọn ngẫu nhiên 3 phần tử của tập S. Tính xác suất để tập hợp con chọn được có tổng các phần tử chia hết cho 3.
 Xem đáp án
Xem đáp án
Chọn B
Không gian mẫu: ![]() .
.
Gọi A là biến cố chọn tập hợp con gồm 3 phần tử và có tổng chia hết cho ![]() .
.
Trường hợp 1: Có 5 số trong tập S chia hết cho 3 nên chọn 3 phần tử có cách chọn.
Trường hợp 2: Có 6 số trong tập S chia hết cho 3 dư 1 nên chọn 3 phần tử có cách chọn.
Trường hợp 3: Có 6 số trong tập S chia hết cho 3 dư 2 nên chọn 3 phần tử có cách chọn.
Trường hợp 4: Chọn một phần tử trong tập S chia hết cho 3, một phần tử trong tập S chia hết cho 3 dư 1, một phần tử trong tập S chia hết cho 3 dư . Suy ra có 5.6.6 cách chọn.
Vậy xác suất cần tìm là P(A) 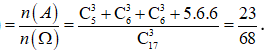 .
.
Câu 21:
Gọi S là tập tất cả các số tự nhiên gồm sáu chữ số được tạo thành từ các chữ số 1, 2, 3, 4, trong đó chữ số 1 có mặt đúng 3 lần, các chữ số còn lại mỗi chữ số có mặt đúng một lần. Chọn ngẫu nhiên một số từ tập S. Tính xác suất để số được chọn không có hai chữ số 1 nào đứng cạnh nhau.
 Xem đáp án
Xem đáp án
Chọn C
Ta có ![]() (vì chữ số 1 có mặt đúng 3 lần).
(vì chữ số 1 có mặt đúng 3 lần).
|
|
2 |
|
3 |
|
4 |
|
Xếp ngẫu nhiên 3 chữ số 2, 3, 4 có ![]() (cách). Vì 3 chữ số 2, 3, 4 sau khi xếp sẽ có 4 vách ngăn (gồm 2 vách ngăn giữa và 2 vách ngăn đầu) nên số cách xếp các chữ số 1 không kề nhau tương ứng số cách xếp các chữ số 1 vào các vách ngăn là: (cách).
(cách). Vì 3 chữ số 2, 3, 4 sau khi xếp sẽ có 4 vách ngăn (gồm 2 vách ngăn giữa và 2 vách ngăn đầu) nên số cách xếp các chữ số 1 không kề nhau tương ứng số cách xếp các chữ số 1 vào các vách ngăn là: (cách).
Vậy xác suất cần tính là:
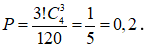
Câu 22:
Có hai dãy ghế đối diện nhau, mỗi dãy có 5 ghế. Xếp ngẫu nhiên 10 học sinh, gồm 5 nam và 5 nữ ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Tính xác suất để mỗi học sinh nam đều ngồi đối diện một học sinh nữ.
 Xem đáp án
Xem đáp án
Chọn C
Số phần tử của không gian mẫu: .
Gọi biến cố : “Xếp 10 học sinh vào 10 ghế sao cho mỗi học sinh nam đều ngồi đối diện một học sinh nữ”.
Giả sử đánh vị trí ngồi như bảng sau:
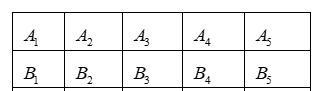
Cách 1: Xếp vị trí có 10 cách. Mỗi cách xếp vị trí sẽ có 5 cách xếp vị trí .
Mỗi cách xếp vị trí , có 8 cách xếp vị trí , tương ứng sẽ có 4 cách xếp vị trí .
Cứ làm như vậy thì số cách xếp thỏa mãn biến cố là:
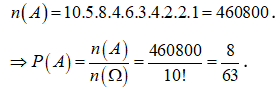
Cách 2: Đánh số cặp ghế đối diện nhau là C1, C2, C3, C4, C5
Xếp bạn nam vào 5 cặp ghế có 5! cách.
Ở mỗi cặp ghế, ta có 2 cách xếp một cặp nam, nữ ngồi đối diện.
Số phần tử của A là: ![]()
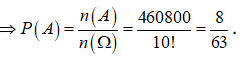
Câu 23:
Một hộp chứa 3 bi xanh, 4 bi đỏ và 5 bi vàng có kích thước khác nhau. Chọn ngẫu nhiên từ hộp đó 4 viên bi. Xác suất để 4 viên bi lấy ra có đủ ba màu là
 Xem đáp án
Xem đáp án
Chọn D
Chọn ngẫu nhiên 4 viên bi từ hộp có 12 viên bi thì có ![]()
Số cách lấy để được đủ ba màu là ![]()
Xác suất để 4 viên bi lấy ra có đủ ba màu bằng
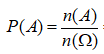
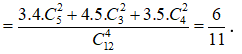
Câu 24:
Raashan, Sylvia và Ted cùng chơi một trò chơi. Mỗi người bắt đầu với 1$. Chuông reo sau mỗi 15 giây, tại thời điểm đó mỗi người chơi mà đang có tiền sẽ chọn ngẫu nhiên một trong hai người còn lại để đưa 1$ (Ví dụ sau khi chuông reo lần thứ nhất, Raashan và Ted có thể cùng đưa cho Sylvia và Sylvia có thể đưa tiền của cô ấy cho Ted, khi đó Raashan có 0$, Sylvia có 2$ và Ted có 1$. Đến vòng thứ hai, Raashan không có tiền để đưa nhưng Sylvia và Ted có thể chọn đưa cho nhau 1$…). Xác suất để sau 2019 lần chuông reo, mỗi người chơi có 1$ là bao nhiêu?
 Xem đáp án
Xem đáp án
Chọn D
Sau khi chia tiền lần đầu tiên sẽ có 8 trường hợp xảy ra như sau:
|
Raashan |
Sylvia |
Ted |
|
1 |
1 |
1 |
|
1 |
1 |
1 |
|
2 |
1 |
0 |
|
2 |
0 |
1 |
|
1 |
2 |
0 |
|
0 |
2 |
1 |
|
1 |
0 |
2 |
|
0 |
1 |
2 |
Các số lần lượt là số tiền của mỗi bạn. Có hai trường hợp cho kết quả (1;1;1) đó là RaashanSylviaTed Raashan hoặc Raashan Ted Sylvia Raashan.
Với mỗi trường hợp cho kết quả (1;1;1) thì lượt chơi tiếp theo sẽ có cơ hội để số tiền mỗi người bằng nhau.
Đối với trường hợp một người có 2$, một người có 1$ và người còn lại không có tiền thì lượt chơi thứ hai sẽ có 4 trường hợp xảy ra. Không mất tính tổng quát ta giả sử Raashan có 2$, Sylvia có 1$ và Ted không có tiền, ta có những cách chuyển tiền như sau:
- Raashan Sylvia và Ted không nhận được tiền.
Raashan Sylvia Ted.
- Raashan Ted Sylvia.
- Sylvia Raashan Ted.
Như vậy trong 4 khả năng trên chỉ có một khả năng cho kết quả (1;1;1) chiếm tỉ lệ
Cứ tiếp tục chơi như vậy đến lượt thứ 2019. Khi đó xác suất mỗi người chơi có 1$ là
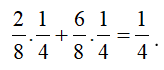
Câu 25:
Có 3 quyển sách toán, 4 quyển sách lý và 5 quyển sách hóa khác nhau được sắp xếp ngẫu nhiên lên một giá sách có 3 ngăn, các quyển sách được sắp dựng đứng thành một hàng dọc vào một trong 3 ngăn ( mỗi ngăn đủ rộng để chứa tất cả các quyển sách). Tính xác suất để không có bất kỳ hai quyển sách toán nào đứng cạnh nhau.
 Xem đáp án
Xem đáp án
Chọn D
Tổng có 3 + 4 + 5 = 12 quyển sách được sắp xếp lên một giá sách có 3 ngăn (có 2 vách ngăn). Vì vậy, ta coi 2 vách ngăn này như 2 quyển sách giống nhau. Vậy số phần tử không gian mẫu ![]()
Gọi A là biến cố : “ Sắp xếp các 12 quyển sách lên giá sao cho không có bất kỳ hai quyển sách toán nào đứng cạnh nhau”.
+) Xếp 9 quyển sách ( lý và hóa) cùng 2 vách ngăn có cách
+) Lúc này, có 12 “khoảng trống” ( do 9 quyển sách ( lý và hóa) cùng 2 vách ngăn tạo ra) để xếp 3 quyển sách toán vào sao cho mỗi quyển vào một “khoảng trống” có cách.
Vậy có tất cả . cách. Suy ra 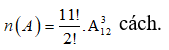
Vậy xác suất để không có bất kỳ hai quyển sách toán nào đứng cạnh nhau là:
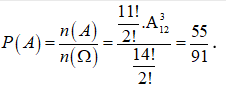
Câu 26:
Gọi S là tập tất cả các số tự nhiên có bốn chữ số khác nhau. Chọn ngẫu nhiên một số từ tập S, tính xác suất để số được chọn lớn hơn số 6700.
 Xem đáp án
Xem đáp án
Chọn A
Gọi số tự nhiên có bốn chữ số thỏa mãn yêu cầu bài toán là ![]()
Số phần tử của không gian mẫu là ![]()
Gọi biến cố A ‘‘Số được chọn lớn hơn số 6700’’.
Ta các TH sau:
TH1: có 1 cách chọn.
![]() có 3 cách chọn.
có 3 cách chọn.
+ Các chữ số c,d được chọn từ 8 chữ số còn lại có sắp thứ tự và số cách chọn là
Số cách để chọn ở trường hợp 1 là: 3.
TH2 : ![]() có 3 cách chọn. Khi đó: b,c,d có cách chọn.
có 3 cách chọn. Khi đó: b,c,d có cách chọn.
Số cách để chọn ở trường hợp 1 là: 3.
Như vậy, ta được n(A) = 3. + 3. = 1680
Suy ra 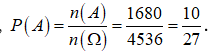
Câu 27:
Tại trạm xe buýt có 5 hành khách đang chờ xe đón, trong đó có A và B. Khi đó có 1 chiếc xe ghé trạm để đón khách, biết rằng lúc đó trên xe chỉ còn đúng 5 ghế trống mỗi ghế trống chỉ 1 người ngồi như hình vẽ bên, trong đó các ghế trống được ghi 1;2;3;4;5 như hình vẽ.
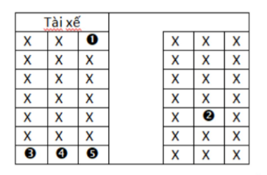
5 hành khách lên xe ngồi ngẫu nhiên vào 5 ghế còn trống, xác suất để A và B ngồi cạnh nhau bằng
 Xem đáp án
Xem đáp án
Chọn B
Số cách xếp ngẫu nhiên là 5! cách.
Ta tìm số cách xếp thoả mãn:
+ Chọn 2 vị trí cạnh nhau (3,4) và (4,5) có 2 cách.
+ Xếp A và B vào 2 vị trí cạnh nhau vừa chọn có 2! cách.
+ Xếp 3 người còn lại có 3! cách.
Số cách xếp là 2.2!3!. Xác suất cần tính bằng 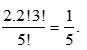
Câu 28:
Gọi S là tập hợp các số tự nhiên có ba chữ số (không nhất thiết khác nhau) được lập từ các chữ số 0;1;2;3;4;5;6;7;8;9. Chọn ngẫu nhiên một số từ S. Tính xác suất để số được chọn thỏa mãn abc
 Xem đáp án
Xem đáp án
Chọn B
Số phần tử của không gian mẫu ![]()
Gọi biến cố A” Chọn được một số thỏa mãn ![]() ”.
”.
Vì mà nên trong các chữ số sẽ không có số 0.
TH1: Số được chọn có chữ số giống nhau có 9 số.
TH2: Số được chọn tạo bới hai chữ số khác nhau.
Số cách chọn ra 2 chữ số khác nhau từ 9 chữ số trên là: .
Mỗi bộ 2 chữ số được chọn tạo ra 2 số thỏa mãn yêu cầu.
Vậy có 2. số thỏa mãn.
TH3: Số được chọn tạo bởi ba chữ số khác nhau.
Số cách chọn ra 3 chữ số khác nhau từ 9 chữ số trên là: .
Mỗi bộ 3 chữ số được chọn chỉ tạo ra một số thỏa mãn yêu cầu.
Vậy có số thỏa mãn.
Vậy ![]()
Xác suất của biến cố A là: .
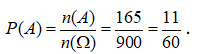
Câu 29:
Trong một lớp học có hai tổ. Tổ 1 gồm 8 học sinh nam và 7 học sinh nữ. Tổ 2 gồm 5 học sinh nam và 7 học sinh nữ. Chọn ngẫu nhiên mỗi tổ hai em học sinh. Xác suất để trong bốn em được chọn có 2 nam và 2 nữ bằng
 Xem đáp án
Xem đáp án
Chọn C
Chọn mỗi tổ hai học sinh nên số phần tử của không gian mẫu là ![]()
Gọi biến cố A: “Chọn 4 học sinh từ 2 tổ sao cho 4 em được chọn có 2 nam và 2 nữ”
Khi đó, xảy ra các trường hợp sau:
TH1: Chọn 2 nam ở Tổ 1, 2 nữ ở Tổ 2. Số cách chọn là ![]()
TH2: Chọn 2 nữ ở Tổ 1, 2 nam ở Tổ 2. Số cách chọn là ![]() .
.
TH3: Chọn ở mỗi tổ 1 nam và 1 nữ. Số cách chọn là ![]()
Suy ra, n(A) = ![]()
Xác suất để xảy ra biến cố A là: ![]()
Câu 30:
Có hai hộp đựng bi, mỗi viên bi chỉ mang một màu trắng hoặc đen. Lấy ngẫu nhiên từ mỗi hộp đúng một viên bi. Biết tổng số bi ở hai hộp là 20 và xác suất để lấy được hai viên bi đen là . Tính xác suất để lấy được hai viên bi trắng.
 Xem đáp án
Xem đáp án
Chọn D
Giả sử hộp 1 có viên bi, trong đó có a viên bi đen.
Hộp 2 có y viên bi, trong đó có b viên bi đen.
x, y, a, b là những số nguyên dương, ![]() )
)
Từ giả thiết x + y = 20, 
Từ đó ta có xy chia hết cho 84
Mặt khác ![]() suy ra xy = 84 ta được x = 14, y = 6
suy ra xy = 84 ta được x = 14, y = 6
Thay vào (1) ta được ab = 55 nên a là ước của 55. Do a14 nên a = 11 suy ra b = 5.
Vậy xác suất để lấy được 2 bi trắng 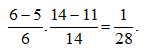
Câu 31:
Có 8 người khách bước ngẫu nhiên vào một cửa hàng có 3 quầy. Tính xác suất để 3 người cùng đến quầy thứ nhất.
 Xem đáp án
Xem đáp án
Chọn D
Số phần tử không gian mẫu: ![]()
Gọi A là biến cố: Có 3 người cùng đến quầy thứ nhất .
Số kết quả thuận lợi của biến cố A là: ![]()
Xác suất của biến cố A: 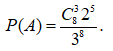
Câu 32:
Đoàn trường THPT Nguyễn Đình Liễn tổ chức giao lưu bóng chuyền học sinh giữa các lớp nhân dịp chào mừng ngày 26/3. Sau quá trình đăng kí có 10 đội tham gia thi đấu từ 10 lớp, trong đó có lớp 10A1 và 10A2. Các đội chia làm hai bảng, kí hiệu là bảng A và bảng B, mỗi bảng 5 đội. Việc chia bảng được thực hiện bằng cách bốc thăm ngẫu nhiên. Tính xác suất để 2 đội 10A1 và 10A2 thuộc hai bảng đấu khác nhau.
 Xem đáp án
Xem đáp án
Chọn A
+ Chia đều 10 đội vào 2 bảng A và B có ![]() cách.
cách.
Do đó số phần tử của không gian mẫu là : ![]()
+ Sắp xếp đội của lớp 10A1 và 10A2 vào 2 bảng khác nhau A và B có 2! cách.
Chọn 4 đội trong 8 đội còn lại để xếp vào bảng có đội lớp 10A1 có cách.
Bốn đội còn lại xếp vào bảng còn lại.
Suy ra số cách chia đều 10 đội vào 2 bảng sao cho 2 đội 10A1 và 10A2 nằm ở 2 bảng khác nhau là ![]()
Gọi A là biến cố “Chia đều 10 đội vào 2 bảng sao cho 2 đội 10A1 và 10A2 nằm ở 2 bảng khác nhau ” thì số các kết quả thuận lợi cho biến cố A là: ![]()
+ Xác suất cần tìm là: 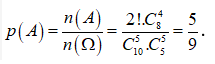
Câu 33:
Gieo ngẫu nhiên một con súc sắc 3 lần liên tiếp. Gọi a,b,c lần lượt là số chấm xuất hiện ở 3 lần gieo. Xác suất của biến cố “ số chia hết cho 45” là
 Xem đáp án
Xem đáp án
Chọn C
Không gian mẫu: “ gieo ngẫu nhiên một con súc sắc 3 lần liên tiếp”
![]()
Biến cố A: “ số chia hết cho 45”
chia hết cho 45 chia hết cho cả 5 và 9
Vì chia hết cho 5 nên ![]() là số chấm xuất hiện của súc sắc khi gieo).
là số chấm xuất hiện của súc sắc khi gieo).
Vì chia hết cho 9 mà c = 5 => a + b + 5 chia hết cho 9.
Các cặp số (a;b) sao cho ![]() mà a+b+5 chia hết cho 9 là: (1;3), (3;1), (2;2)
mà a+b+5 chia hết cho 9 là: (1;3), (3;1), (2;2)
Do đó: n(A) = 3.
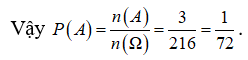
Câu 34:
Sắp ngẫu nhiên 5 học sinh nam và học sinh nữ thành một hàng ngang. Tính xác suất để không có học sinh nữ nào đứng cạnh nhau.
 Xem đáp án
Xem đáp án
Chọn B
Số phần tử của không gian mẫu là ![]()
Sắp 5 học sinh nam thành một hàng ngang, có 5! cách (tạo ra khoảng trống).
Chọn 3 khoảng trống trong 6 khoảng trống để xếp 3 nữ, có cách chọn. Khi đó, số cách xếp 3 bạn nữ là .3! cách.
Vậy xác suất cần tìm là 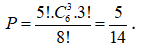
Câu 35:
Một đoàn tàu gồm ba toa đỗ sân ga. Có 5 hành khách lên tàu. Mỗi hành khách độc lập với nhau. Chọn ngẫu nhiên một toa. Tìm xác suất để mỗi toa có ít nhất 1 hành khách bước lên tàu.
 Xem đáp án
Xem đáp án
Chọn A
Số phần tử không gian mẫu: ![]()
Gọi A là biến cố: Mỗi toa có ít nhất một khách lên tàu .
Có hai trường hợp:
TH1: Một toa có 3 khách 2 toa còn lại mỗi toa có 1 khách.
Trường hợp này có: ![]() (cách).
(cách).
TH 2: Một toa có 1 khách 2 toa còn lại mỗi toa có 2 khách.
Trường hợp này có:![]() (cách).
(cách).
Số kết quả thuận lợi của biến cố A là: n(A) = 150(cách).
Xác suất của biến cố A : ![]()
Câu 36:
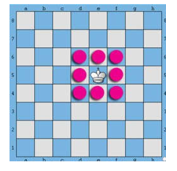
Một quân vua được đặt ở một ô giữa bàn cờ vua. Mỗi bước di chuyển, quân vua được chuyển sang một ô khác chung cạnh hoặc chung đỉnh với ô đang đứng ( xem hình minh họa). Bạn An di chuyển quân vua ngẫu nhiên bước. Xác suất để sau bước đi quân vua trở về ô ban đầu là
 Xem đáp án
Xem đáp án
Chọn A
Không gian mẫu là
Có hai trường hợp
+ Trường hợp 1: Bước 1 đi 4 ô góc thì bước 2 có 2 cách đi, bước 3 có 1 cách đi
+ Trường hợp 2: Bước 1 đi 4 ô còn lại thì bước 2 có 4 cách đi, bước 3 có 1 cách đi
Vậy tât cả có 4.2 + 4.4 = 24
Suy ra xác suất để sau 3 bước đi quân vua trở về ô ban đầu là: 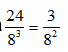
Câu 37:
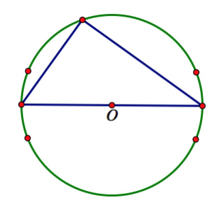
Cho đa giác đều 20 cạnh. Lấy ngẫu nhiên 3 đỉnh của đa giác đều. Xác suất để 3 đỉnh lấy được là 3 đỉnh của một tam giác vuông không có cạnh nào là cạnh của đa giác đều bằng
 Xem đáp án
Xem đáp án
Chọn C
Đa giác đều nội tiếp một đường tròn tâm O. Lấy ngẫu nhiên 3 đỉnh có cách.
Để 3 đỉnh là 3 đỉnh một tam giác vuông không có cạnh nào là cạnh của đa giác đều thực hiện theo các bước:
Lấy một đường kính qua tâm đường tròn có 10 cách ta được 2 đỉnh.
Chọn đỉnh còn lại trong 20 - 2 - 4 = 14 đỉnh (loại đi 2 đỉnh thuộc đường kính và 4 đỉnh gần ngay đường kính đó) cách.
Vậy có tất cả 10.14 = 140 tam giác thoả mãn.
Xác suất cần tính bằng 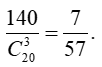
Câu 38:
Năm đoạn thẳng có độ dài 1 cm; 3 cm; 5 cm; 7 cm; 9 cm. Lấy ngẫu nhiên ba đoạn thẳng trong năm đoạn thẳng trên. Xác suất để ba đoạn thẳng lấy ra tạo thành ba cạnh của một tam giác bằng
 Xem đáp án
Xem đáp án
Chọn D
Lấy ba đoạn thẳng từ năm đoạn thẳng có = 10 cách. Suy ra số phần tử của không gian mẫu là ![]()
Gọi A là biến cố: " Ba đoạn thẳng lấy ra tạo thành ba cạnh của một tam giác ".
Khi đó 3 đoạn thẳng được chọn thỏa mãn tính chất: Tổng độ dài 2 đoạn thẳng luôn lớn hơn độ dài đoạn thẳng còn lại.
Có 3 bộ thỏa mãn là ![]()
Vậy xác suất để ba đoạn thẳng lấy ra tạo thành ba cạnh của một tam giác là
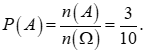
Câu 39:
Trong một phòng học, có 36 cái bàn rời nhau được đánh số từ 1 đến 36, mỗi bàn dành cho 1 học sinh. Các bàn được xếp thành một hình vuông có kích thước 6x6. Cô giáo xếp tuỳ ý 36 học sinh của lớp vào các bàn, trong đó có hai bạn A và B. Xác suất để A và B ngồi ở hai bàn xếp cạnh nhau bằng (theo chiều ngang hoặc chiều dọc).
 Xem đáp án
Xem đáp án
Chọn A
Gọi A là biến cố: Xếp hai học sinh A, B ngồi ở hai bàn xếp cạnh nhau.
Số cách xếp ngẫu nhiên học sinh vào 36 cái bàn là 36!, ![]()
Ta tìm số cách xếp thuận lợi cho biến cố :
- Chọn 1 hàng hoặc 1 cột có cách;
- Mỗi hàng hoặc cột đều có 6 bàn nên có 5 cặp bàn xếp kề nhau, chọn lấy 1 trong 5 cặp bàn cạnh nhau trong hàng hoặc cột vừa chọn ra có cách;
- Xếp A và B vào cặp bàn vừa chọn có 2! cách;
- Xếp 34 học sinh còn lại có 34! cách.
Vậy tổng số cách xếp thoả mãn là: ![]()
Vậy xác suất cần tính: 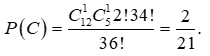
Câu 40:
Có hai dãy ghế đối diện nhau, mỗi dãy có năm ghế. Xếp ngẫu nhiên 10 học sinh, gồm 5 nam và 5 nữ ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ và bất kì hai học sinh ngồi liền kề nhau thì khác phái bằng
 Xem đáp án
Xem đáp án
Chọn D
Cách 1. Xếp ngẫu nhiên 10 học sinh vào hai dãy ghế có cách.
Đánh số ghế lần lượt từ 1 đến 10.
Xếp học sinh thỏa mãn bài toán xảy ra hai khả năng sau:
Khả năng 1: Nam ngồi vị trí lẻ, nữ ngồi vị trí chẵn có 5!.5! cách.
Khả năng 2: Nam ngồi vị trí chẵn, nữ ngồi vị trí lẻ có 5!.5! cách.
Vậy có tất cả 2. cách.
Xác suất cần tìm bằng 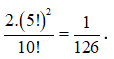
Cách 2: Xếp ngẫu nhiên 10 học sinh vào hai dãy ghế, có 10! cách xếp.
Ta chia hai dãy ghế thành 5 cặp ghế đối diện:
+ Chọn 1 nam và 1 nữ xếp vào cặp ghế 1 có ![]() cách;
cách;
+ Chọn 1 nam và 1 nữ xếp vào cặp ghế 2 có ![]() cách;
cách;
+ Chọn 1 nam và 1 nữ xếp vào cặp ghế 3 có ![]() cách;
cách;
+ Chọn 1 nam và 1 nữ xếp vào cặp ghế 4 có ![]() cách;
cách;
+ Chọn 1 nam và 1 nữ xếp vào cặp ghế 5 có 1 cách.
Vậy có tất cả ![]() cách xếp thỏa mãn.
cách xếp thỏa mãn.
Xác suất cần tìm bằng 
