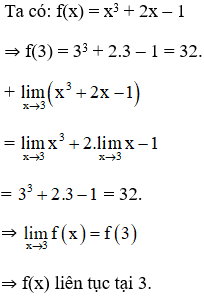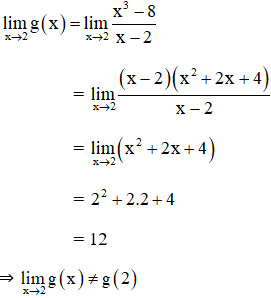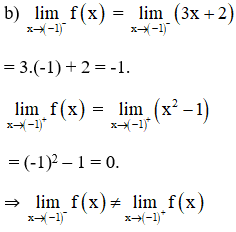Bài 3: Hàm số liên tục
-
1339 lượt thi
-
6 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 2:
a) Xét tính liên tục của hàm số y = g(x) tại x0 = 2, biết :
b) Trong biểu thức g(x) ở trên, cần thay số 5 bởi số nào đó để hàm số liên tục tại x0=2.
Xem đáp án
Lời giải:
a) Ta có: g(2) = 5.
⇒ g(x) không liên tục tại x = 2.
b) Để g(x) liên tục tại x = 2
Vậy để hàm số liên tục tại x = 2 thì cần thay 5 bằng 12.
Câu 3:
Cho hàm số
a. Vẽ đồ thị hàm số y= f(x). Từ đó nêu nhận xét về tính liên tục của hàm số trên tập xác định của nó.
b. Khẳng định nhận xét trên bằng 1 chứng minh.
Xem đáp án
Lời giải:
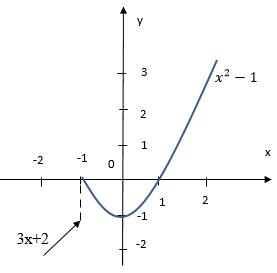
a) Đồ thị hàm số (hình bên).
Quan sát đồ thị nhận thấy :
+ f(x) liên tục trên các khoảng (-∞ ; -1) và (-1 ; ∞).
+ f(x) không liên tục tại x = -1.
⇒ không tồn tại giới hạn của f(x) tại x = -1.
⇒ Hàm số không liên tục tại x = -1.
Câu 4:
Cho các hàm số và
Với mỗi hàm số, hãy xác định các khoảng trên đó hàm liên tục.
Xem đáp án
Lời giải:
Câu 5:
Ý kiến sau đúng hay sai?
"Nếu hàm số y = f(x) liên tục tại điểm x0 và hàm số y = g(x) không liên tục tại x0, thì y = f(x) + g(x) là một hàm số không liên tục tại x0".
Xem đáp án
Lời giải:
Ý kiến trên đúng.
Vì giả sử ngược lại hàm số y = h(x) = f(x) + g(x) là hàm số liên tục tại x0. Khi đó, hàm số g(x) = h(x) – f(x) là hiệu của hai hàm số liên tục tại x0 nên hàm số g(x) là hàm số liên tục x0 ( định lí về hàm số liên tục).
=> Mâu thuẫn với giả thiết là hàm số g(x) không liên tục tại x0.
Câu 6:
a. 2x3 – 6x + 1 = 0 có ít nhất hai nghiệm.
b. cos(x) = x có nghiệm
Xem đáp án
Lời giải:
a. Đặt f(x) = 2x3 – 6x + 1
TXĐ: D = R
f(x) là hàm đa thức nên liên tục trên R.
Ta có: f(-2) = 2.(-2)3 – 6(-2) + 1 = - 3 < 0
f(0) = 1 > 0
f(1) = 2.13 – 6.1 + 1 = -3 < 0.
⇒ f(-2).f(0) < 0 và f(0).f(1) < 0
⇒ f(x) = 0 có ít nhất một nghiệm thuộc khoảng (-2; 0) và ít nhất một nghiệm thuộc (0 ; 1)
⇒ phương trình f(x) = 0 có ít nhất hai nghiệm.
b. Xét hàm số g(x) = x – cos x liên tục trên R.
do đó liên tục trên đoạn [-π; π] ta có:
g(-π) = -π – cos (-π) = -π + 1 < 0
g(π) = π – cos π = π – (-1) = π + 1 > 0
⇒ g(-π). g(π) < 0
⇒ Phương trình x – cos x = 0 có nghiệm trong (-π; π) tức là cos x = x có nghiệm.