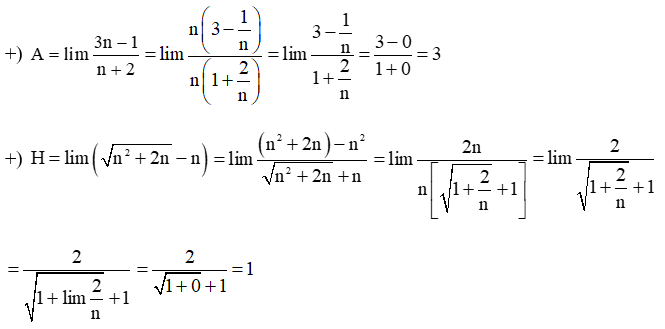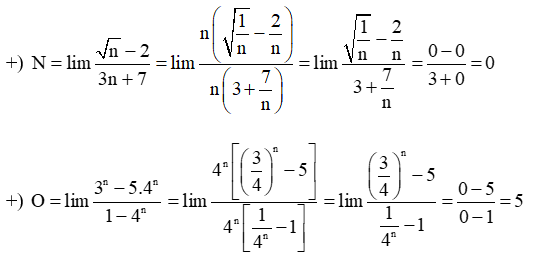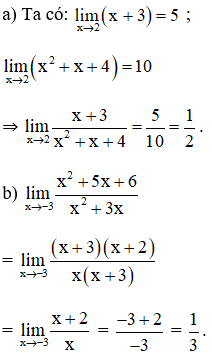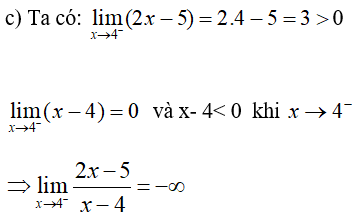Ôn tập chương 4
-
1436 lượt thi
-
8 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Hãy lập bảng liệt kê các giới hạn đặc biệt của dãy số và giới hạn đặc biệt của hàm số.
 Xem đáp án
Xem đáp án
Lời giải:
Câu 2:
Cho hai dãy số (un) và (vn). Biết |un – 2| ≤ vn với mọi n và lim vn = 0. Có kết luận gì về giới hạn của dãy số (un)?
 Xem đáp án
Xem đáp án
Lời giải:
Lấy số dương ε bé tùy ý bất kì:
⇒ có một số n0 thỏa mãn: |vn| < ε kể từ n = n0.
⇒ |un – 2| < vn < |vn| < ε kể từ n = n0 trở đi
⇒ lim (un – 2) = 0
⇒ lim un = 2.
Câu 3:
Tên một học sinh được mã hóa bởi số 1530. Biết rằng mỗi chữ số trong số này là giá trị một trong các biểu thức A, H, N, O với
Hãy cho biết tên của học sinh này, bằng cách thay các chữ số trên bởi các chữ kí hiệu biểu thức tương ứng.
 Xem đáp án
Xem đáp án
Lời giải:
Khi thay đổi chữ số 1530 bởi các biểu thức giới hạn tương ứng ta được chữ HOAN là tên các bạn học sinh đã cho.
Câu 4:
a. Có nhận xét gì về công bội của các cấp số nhân lùi vô hạn?
b. Cho ví dụ về một cấp số nhân lùi vô hạn và có công bội là số âm và một cấp số nhân lùi vô hạn có công bội là số dương và tính tổng của các cấp số nhân đó.
 Xem đáp án
Xem đáp án
Lời giải:
a) Cấp số nhân vô hạn với công bội q mà |q| < 1 là cấp số nhân lùi vô hạn
b) Ví dụ về cấp số nhân lùi vô hạn có công bội âm:
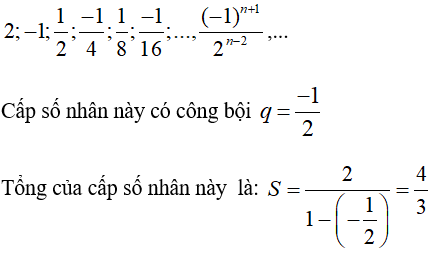
Câu 6:
Cho hai hàm số và
a. Tính , , ,
b. Hai đường cong dưới đây là đồ thị của hai hàm số đã cho. Từ kết quả câu a), hãy xác định xem con đường cong nào là đồ thị của mỗi hàm số đó.
 Xem đáp án
Xem đáp án
Lời giải:
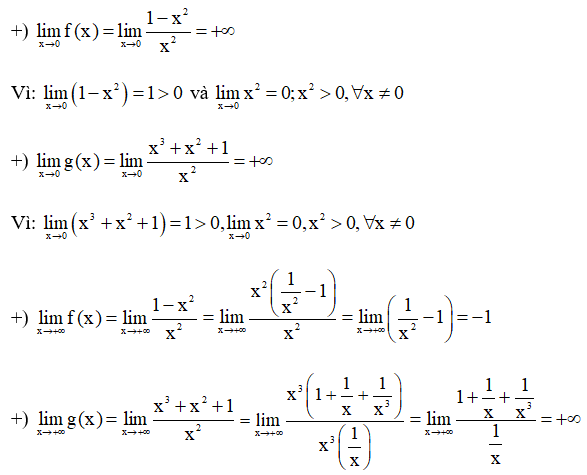

b) Nhận thấy hình a) khi x → +∞ thì y → +∞
⇒ Hình a) là đồ thị hàm số y = g(x).
Hình b) khi x → +∞ thì y → -1
⇒ Hình b) là đồ thị hàm số y = f(x).
Câu 7:
Xét tính liên tục trên R của hàm số:
 Xem đáp án
Xem đáp án
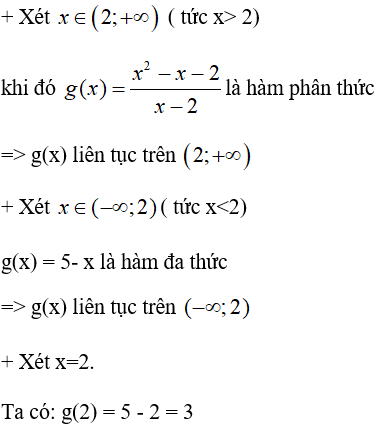
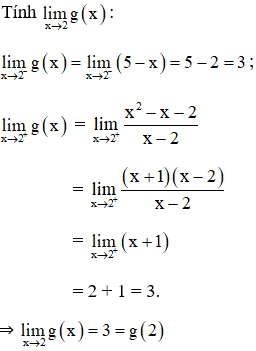
⇒ g(x) liên tục tại 2.
Vậy hàm số g(x) liên tục trên R.
Câu 8:
Chứng minh rằng phương trình x5 – 3x4 + 5x – 2 = 0 có ít nhất ba nghiệm nằm trong khoảng (-2; 5)
 Xem đáp án
Xem đáp án
Lời giải:
Đặt f(x) = x5 – 3x4 + 5x – 2
f(x) là hàm đa thức nên liên tục trên R.
Ta có: f(0) = –2 < 0
f(1) = 1 > 0
f(2) = -8 < 0
f(3) = 13 > 0
⇒ f(0).f(1) < 0; f(1).f(2) < 0; f(2).f(3) < 0
⇒ Phương trình f(x) = 0 có ít nhất 1 nghiệm thuộc khoảng (0; 1); 1 nghiệm thuộc khoảng (1; 2); 1 nghiệm thuộc khoảng (2; 3)
⇒ f(x) = 0 có ít nhất 3 nghiệm thuộc (0; 3) hay f(x) = 0 có ít nhất 3 nghiệm thuộc (-2; 5).