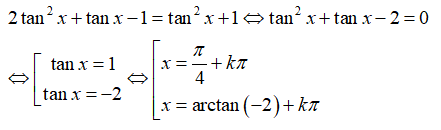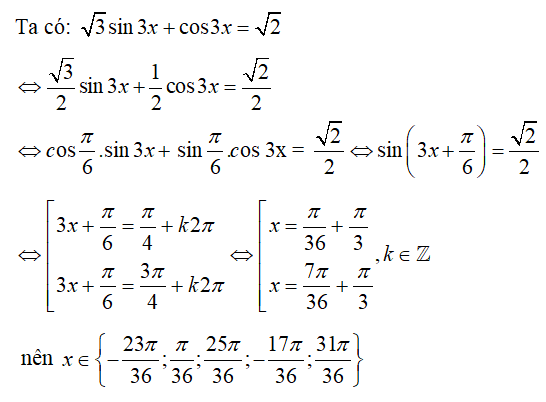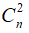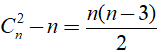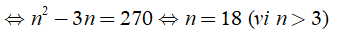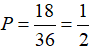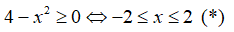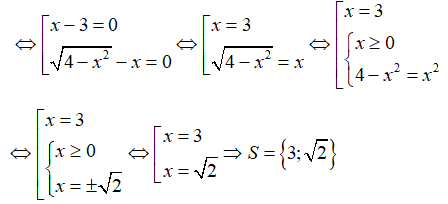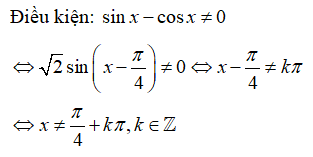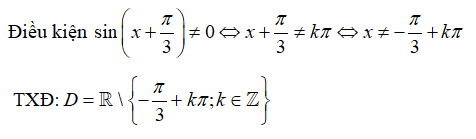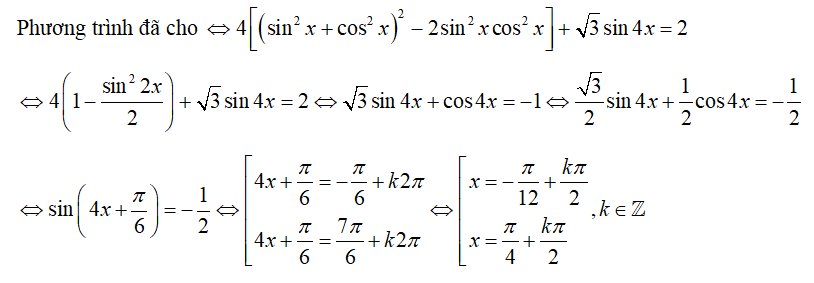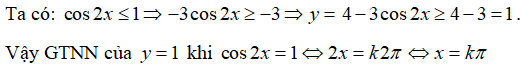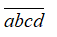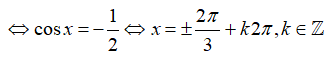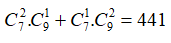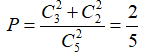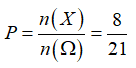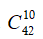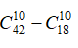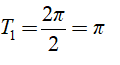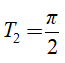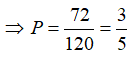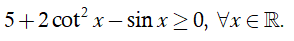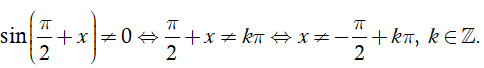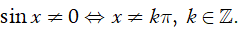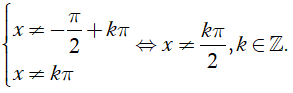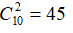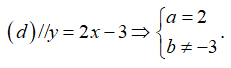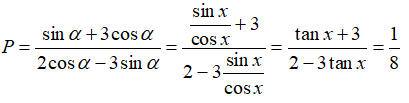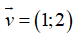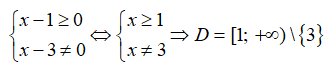Đề thi Toán lớp 11 Học kì 1 (có đáp án) (phần 7)
-
9415 lượt thi
-
50 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Phương trình: 2sin2x+sinx.cosx-cos2x=1 có các nghiệm là
 Xem đáp án
Xem đáp án
Chọn B
Ta thấy cosx = 0 không thỏa mãn phương trình đã cho
chia cả 2 vế của phương trình cho , ta được:
Câu 4:
Cho đa giác đều n đỉnh, . Tìm n biết rằng đa giác đã cho có 135 đường chéo.
 Xem đáp án
Xem đáp án
Chọn D
Đa giác lồi n đỉnh thì có n cạnh. Nếu vẽ tất cả các đoạn thẳng nối từng cặp trong n đỉnh này thì có một bộ gồm các cạnh và các đường chéo.
Vậy để tính số đường chéo thì lấy tổng số đoạn thẳng dựng được trừ đi số cạnh, với
• Tất cả đoạn thẳng dựng được là bằng cách lấy ra 2 điểm bất kỳ trong n điểm, tức là số đoạn thẳng chính là số tổ hợp chập 2 của n phần tử.
Như vậy, tổng số đoạn thẳng là
• Số cạnh của đa giác lồi là n
Suy ra số đường chéo của đa giác đều n đỉnh là
Theo bài ra, ta có 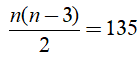
Câu 5:
Phương trình nào sau đây vô nghiệm
 Xem đáp án
Xem đáp án
Chọn B
Các phương trình ở các đáp án A, C và D có nghiệm.
Xét phương trình: 2sinx - 3cosx = 4
Vì nên phương trình vô nghiệm
Câu 6:
Cho đường tròn . Ảnh của đường tròn (C) qua phép là đường tròn có phương trình nào dưới đây?
 Xem đáp án
Xem đáp án
Chọn B
Đường tròn (C) có tâm I(-2;1) và bán kính R = 3
Gọi (C') là ảnh của (C) qua phép ⇒ (C') tâm I'(2'-1) và bán kính R’ = R = 3 .
Khi đó
Câu 7:
Gieo một con xúc sắc cân đối đồng chất hai lần. Tính xác suất sao cho tổng số chấm của hai lần gieo là số lẻ
 Xem đáp án
Xem đáp án
Chọn A
Số phần tử của không gian mẫu là: n(Ω)= 6.6 = 36 (phần tử)
Để tổng số chấm lẻ thì số cách chọn là: 6.3 = 18 (cách)
Xác suất để tổng số chấm của hai lần gieo là số lẻ là:
Câu 8:
Tập nghiệm của phương trình
 Xem đáp án
Xem đáp án
Chọn D
Điều kiện:
Với điều kiện (*) phương trình đã cho
Câu 13:
Lớp 11A7 có 18 nam và 24 nữ. Chọn ngẫu nhiên hai học sinh để hát song ca. Xác suất để trong đó có ít nhất một nam là?
 Xem đáp án
Xem đáp án
Chọn B
Số cách chọn ngẫu nhiên 2 học sinh là: 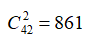
Số cách chọn 2 học sinh để có ít nhất 1 nam là: 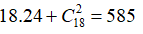
Xác suất để có ít nhất 1 nam là:
Câu 15:
Cho tập A = {0;1;2;3;4;5;6;7}. Từ tập A có thể lập được bao nhiêu số tự nhiên chẵn có bốn chữ số đôi một khác nhau?
 Xem đáp án
Xem đáp án
Chọn D
Gọi số tự nhiên có 4 chữ số thỏa mãn đề bài là
+) Nếu d = 0 thì số cách chọn abc là: 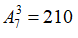
+) Nếu d ∈ {2;4;6} thì a có 6 cách chọn ⇒ số cách chọn là bc là
Trong trường hợp này có: 3.6.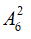
Số các số thỏa mã đề bài là: 210 + 540 = 750 (số)
Câu 16:
Cho đường thẳng . Điểm nào sau đây thuộc đường thẳng (d)
 Xem đáp án
Xem đáp án
Chọn A
Thay điểm x = -1 ⇒ t = 1 ⇒ y = 5 ⇒ điểm (1;-5) ∈ d
Câu 17:
Một tổ gồm 7 nam và 6 nữ. Hỏi có bao nhiêu cách chọn 4 em đi trực nhật sao cho có ít nhất 2 nữ?
 Xem đáp án
Xem đáp án
Chọn B
Có các cách chọn sau:
+) 2 nữ, 2 nam 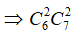
+) 3 nữ, 1 nam 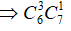
+) 4 nữ 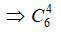
Theo quy tắc cộng, số cách chọn là: 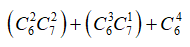
Câu 20:
Cho 2 đường thẳng song song. Trên đường thẳng thứ nhất lấy 7 điểm phân biệt, trên đường thẳng thứ hai lấy 9 điểm phân biệt. Hỏi có bao nhiêu tam giác có các đỉnh thuộc tập 16 điểm đã lấy trên hai đường thẳng trên?
 Xem đáp án
Xem đáp án
Chọn C
TH1. Lấy 2 điểm thuộc ; 1 điểm thuộc có 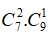
TH2. Lấy 1 điểm thuộc ; 2 điểm thuộc có 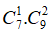
Vậy số tam giác cần tìm là
Câu 21:
Từ một hộp chứa ba quả cầu trắng và hai quả cầu đen, lấy ngẫu nhiên đồng thời hai quả. Tính xác suất để hai quả đó cùng màu
 Xem đáp án
Xem đáp án
Chọn D
Lấy ngẫu nhiên 2 quả cầu trong 5 quả cầu có 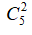
TH1. 2 quả cầu lấy ra cùng màu trắng ⇒ có 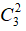
TH1. 2 quả cầu lấy ra cùng màu đen ⇒ có 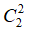
Vậy xác suất cần tính là
Câu 23:
Gieo một đồng xu cân đối và đồng chất liên tiếp ba lần. Gọi A là biến cố “Có ít nhất hai mặt sấp xuất hiện liên tiếp” và B là biến cố “Kết quả ba lần gieo là như nhau”. Xác định biến cố A ∪ B
 Xem đáp án
Xem đáp án
Chọn C
Phần tử của biến cố B là B = {SSS;NNN}
Phần tử của biến cố A là A = {SSN;SSS;NSS} .
Vậy A ∪ B = {SSS;SSN;NSS;NNN}
Câu 25:
Có hai chiếc hộp: Hộp thứ nhất chứa bốn bi xanh, ba bi vàng; Hộp thứ hai chứa hai bi xanh, một bi đỏ. Lấy ngẫu nhiên từ mỗi hộp một viên bi. Xác suất để được hai bi xanh là?
 Xem đáp án
Xem đáp án
Chọn C
Lấy 1 bi từ hộp thứ nhất có 7 cách, 1 bi từ hộp thứ hai có 3 cách ⇒ n(Ω) = 3.7 = 21
Lấy 1 bi xanh từ hộp thứ nhất có 4 cách, 1 bi xanh từ hộp thứ hai có 2 cách ⇒ n(X) = 4.2 = 8
Vậy xác suất cần tính là
Câu 27:
Trong mặt phẳng, với hệ tọa độ Oxy, cho điểm M(1;-3). Phép tịnh tiến theo véctơ biến M thành điểm
 Xem đáp án
Xem đáp án
Chọn C
Câu 28:
Trong mp Oxy cho đường thẳng d có phương trình 3x + y - 3 = 0. Ảnh của đường thẳng d qua phép biến đường thẳng d thành đường thẳng có phương trình là:
 Xem đáp án
Xem đáp án
Chọn B
Câu 29:
Lớp 11A7 có 18 học sinh nam và 24 học sinh nữ. Thầy chủ nhiệm cần chọn 10 học sinh để luyện tập vũ khúc sân trường. Hỏi thầy chủ nhiệm có bao nhiêu cách chọn 10 học sinh sao cho có ít nhất 1 học sinh nữ?
 Xem đáp án
Xem đáp án
Chọn B
Lớp học có tất cả 42 học sinh
Số cách chọn 10 học sinh từ 42 học sinh là
Giả sử trong 10 học sinh được chọn không có học sinh nữ có 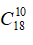
Vậy số cách chọn thỏa mãn yêu cầu bài toán là
Câu 30:
Hàm số y = sin2x - tan2x tuần hoàn với chu kỳ là bao nhiêu?
 Xem đáp án
Xem đáp án
Chọn D
Hàm số y = sin 2x tuần hoàn với chu kì
Hàm số y = tan2x tuần hoàn với chu kì
Do đó; hàm số đã cho tuần hoàn với chu kì T = π
Câu 32:
Sắp xếp 5 người trong đó có An và Linh ngồi vào 5 ghế thẳng hàng. Xác suất để An và Linh không ngồi cạnh nhau là:
 Xem đáp án
Xem đáp án
Chọn D
Sắp xếp 5 người vào 5 ghế có 5! = 120 cách
Giả sử An và Linh ngồi cạnh nhau, khi đó coi An và Linh là một phần tử + 3 người còn lại ngồi vào ghế.
Khi đó, có 2!.4! = 48 cách sắp xếp để An và Linh ngồi cạnh nhau
Vậy có 120 - 48 = 72 cách sắp xếp để An và Linh không ngồi cạnh nhau
Câu 33:
Từ thành phố A tới thành phố B có 4 con đường, từ thành phố B tới thành phố C có 5 con đường. Hỏi có bao nhiêu cách đi từ A tới C qua B chỉ một lần.
 Xem đáp án
Xem đáp án
Chọn B
Đi từ A → B có 4 cách, đi từ B → C có 5 cách.
Theo quy tắc nhân, đi từ A → C có 4 x 5 = 20 cách
Câu 35:
Trong mặt phẳng Oxy cho đường thẳng d có phương trình: . Ảnh của đường thẳng d qua phép tịnh tiến theo véctơ có phương trình:
 Xem đáp án
Xem đáp án
Chọn D
Câu 37:
Tìm tập xác định D của hàm số
 Xem đáp án
Xem đáp án
Chọn A
Hàm số xác định khi và chỉ khi các điều kiện sau thỏa mãn đồng thời
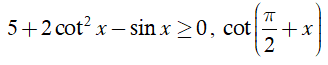
Ta có
⇒
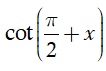
cot x xác định
Do đó hàm số xác định
Vậy tập xác định 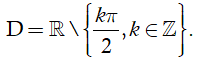
Câu 38:
Để chào mừng ngày 26/3 Đoàn trường THPT XXX tổ chức giải bóng đá có 10 đội tham dự theo thể thức thi đấu vòng tròn tính điểm (hai đội bất kỳ đều gặp nhau đúng 1 trận). Hỏi đoàn trường phải tổ chức bao nhiêu trận đấu?
 Xem đáp án
Xem đáp án
Chọn B
Cứ 2 đội ta sẽ có 1 trận bóng đá
Với 10 đội, đoàn trưởng phải tổ chức số trận là
Câu 39:
Đường thẳng đi qua điểm A(-2;1) và song song với đường thẳng y = 2x - 3 có phương trình là
 Xem đáp án
Xem đáp án
Chọn C
Gọi phương trình đường thẳng cần tìm là (d): y = ax + b
Vì
Mà (d) đi qua A(2;-1) ⇒ -2a + b = 1 ⇔ b = 5
Vậy phương trình đường thẳng d): y = 2x + 5
Câu 40:
Cho tập A = {0;1;2;3;4;5;6;7;8;9}. Số các số tự nhiên có năm chữ số đôi một khác nhau được lấy ra từ tập A là
 Xem đáp án
Xem đáp án
Chọn B
Gọi số cần tìm có dạng 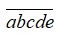
Suy ra a có 9 cách chọn, b có 9 cách chọn, c có 8 cách chọn, d có 7 cách chọn, e có 6 cách chọn.
Khi đó, có tất cả 9.9.8.7.6 = 27216 số cần tìm
Câu 41:
Trong mặt phẳng Oxy cho đường thẳng d có phương trình 2x - 3y + 1 = 0. Để phép tịnh tiến theo vector biến đường thẳng d thành chính nó thì phải là vecto nào trong số các vecto sau ?
 Xem đáp án
Xem đáp án
Chọn A
Giả sử vector 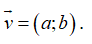
Gọi M(x;y) là điểm thuộc đường thẳng d và M'(x';y') là ảnh của đường thẳng d qua phép tịnh tiến vector 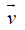
Câu 42:
Một thùng có 7 sản phẩm, trong đó có 4 sản phầm loại I và 3 sản phẩm loại II. Lấy ngẫu nhiên 2 sản phẩm. Xác suất để lấy được 2 sản phẩm cùng loại là
 Xem đáp án
Xem đáp án
Chọn B
Câu 43:
Số hạng không chứa x trong khai triển là
 Xem đáp án
Xem đáp án
Chọn C
Ta có :
Số hạng không chứa x khi 12 - 4k = 0 ⇔ k =3 ⇒ số hạng đó là
Câu 46:
Trong mặt phẳng tọa độ Oxy cho điểm M'(-3;2) là ảnh của điểm M qua phép quay tâm O góc thì điểm M có tọa độ là:
 Xem đáp án
Xem đáp án
Chọn B
Điểm M(-3;2) là ảnh của điểm M(2;3) qua phép quay tâm O góc
Câu 48:
Trong mặt phẳng Oxy cho đường thẳng d: x + 2y - 3 = 0. Hỏi phép dời hình có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k = 2 và phép tịnh tiến theo vector biến d thành đường thẳng d’ có phương trình:
 Xem đáp án
Xem đáp án
Chọn B
Gọi M(x;y) là điểm thuộc đường thẳng d, M'(x';y') là điểm thuộc đường thẳng là ảnh của d qua phép vị tự tâm O tỉ số k = 2, M''(x'';y'') là điểm thuộc đường thẳng d'' là ảnh của qua phép tịnh tiến theo vector