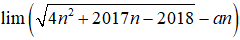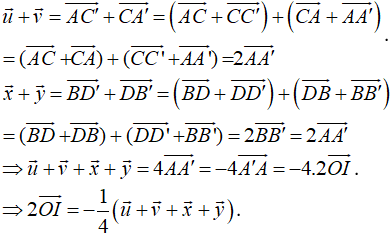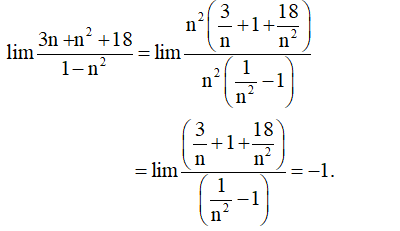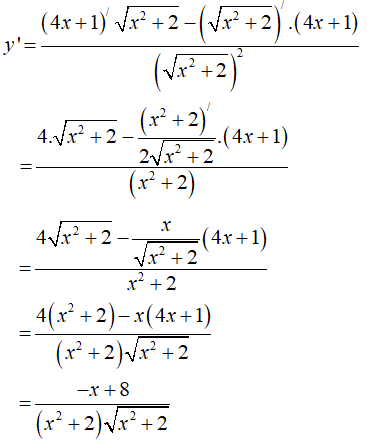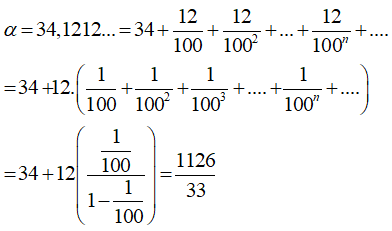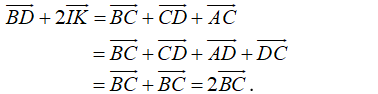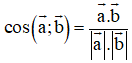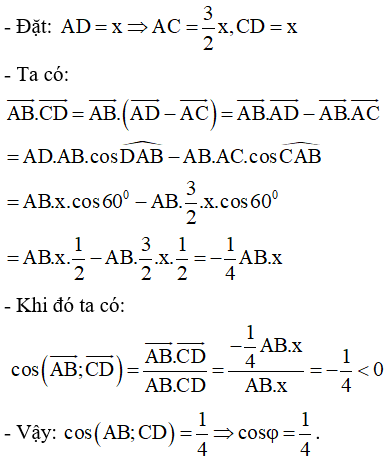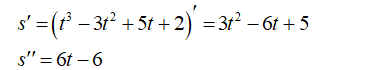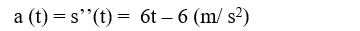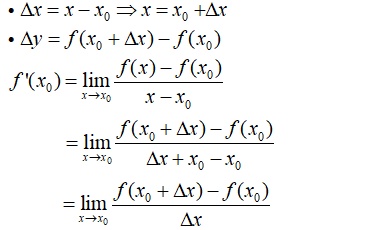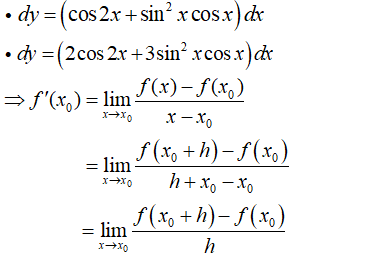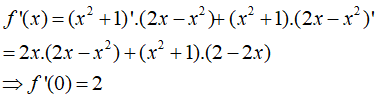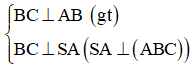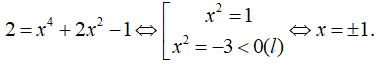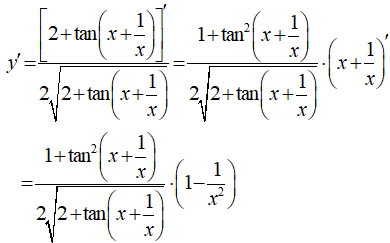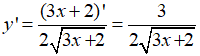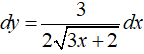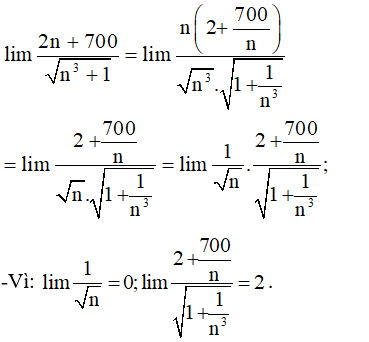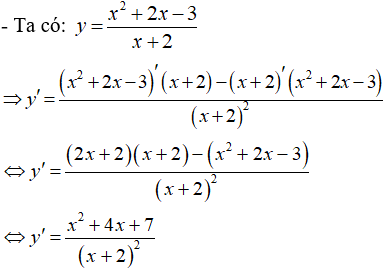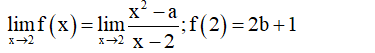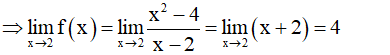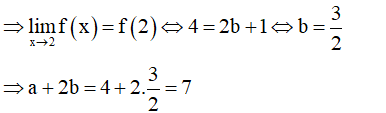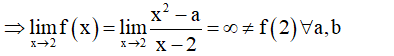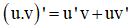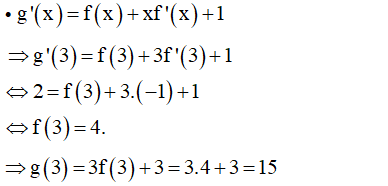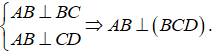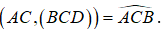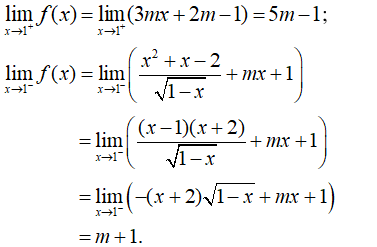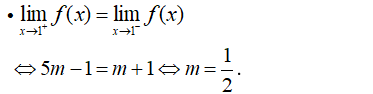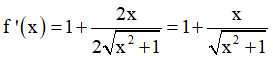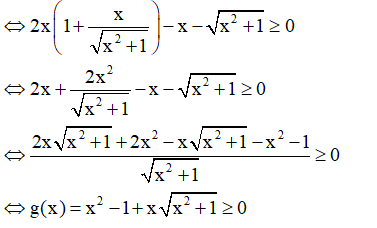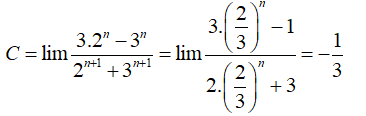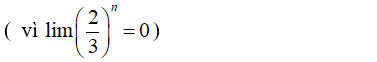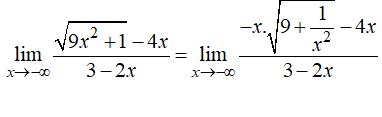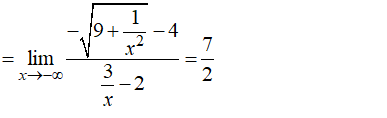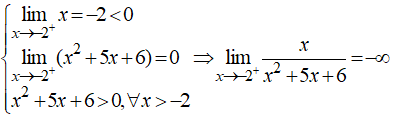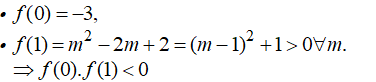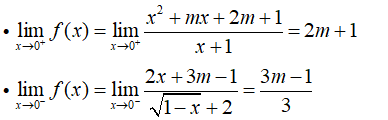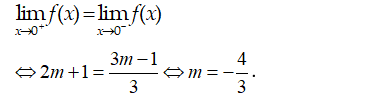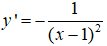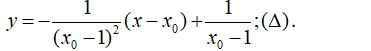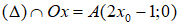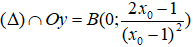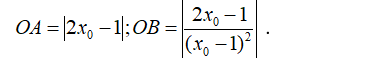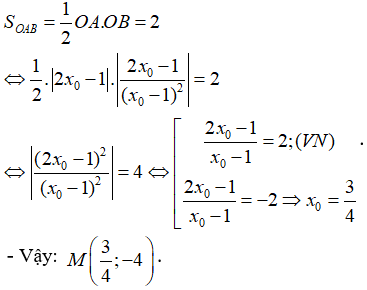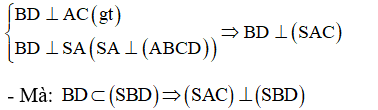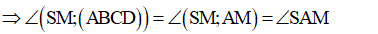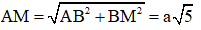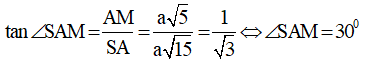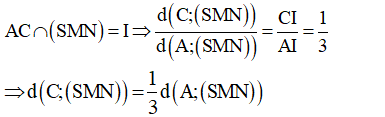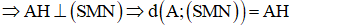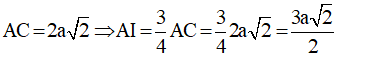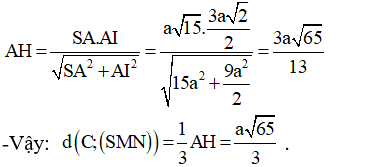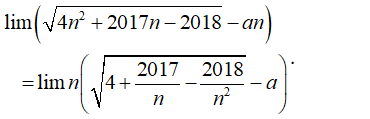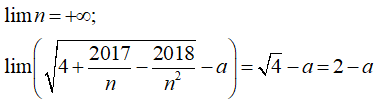35 câu hỏi trắc nghiệm thuộc Đề thi Toán lớp 11 Học kì 2 (có đáp án) (phần 4)

Câu 1:

Phần I: Trắc nghiệm

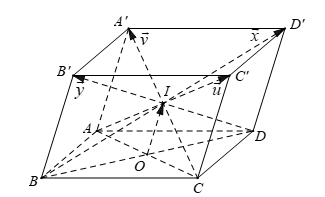
Cho hình hộp ABCD.A'B'C'D' có tâm O. Gọi I là tâm hình bình hành ABCD. Đặt $\vec{A C'} = \vec{u}, \vec{C A'} = \vec{v}, \vec{B D'} = \vec{x}, \vec{D B'} = \vec{y}$ . Khẳng định nào sau đây đúng?

A. $2 \vec{O I} = \frac{1}{2} (\vec{u} + \vec{v} + \vec{x} + \vec{y})$

B. $2 \vec{O I} = - \frac{1}{2} (\vec{u} + \vec{v} + \vec{x} + \vec{y})$

C. $2 \vec{O I} = \frac{1}{4} (\vec{u} + \vec{v} + \vec{x} + \vec{y})$

D. $2 \vec{O I} = - \frac{1}{4} (\vec{u} + \vec{v} + \vec{x} + \vec{y})$

Xem đáp án

Chọn D.

- Ta phân tích:

Câu 2:

$l i m \frac{3 n + n^{2} + 18}{1 - n^{2}}$ bằng

A. 3

B. 18

C. -1

D. 1

Xem đáp án

Đáp án C

Câu 3:

Tính đạo hàm của hàm số $y = \frac{4 x + 1}{\sqrt{x^{2} + 2}}$

A. $\frac{- x}{(x^{2} + 2) \sqrt{x^{2} + 2}}$

B. $\frac{x + 8}{(x^{2} + 2) \sqrt{x^{2} + 2}}$

C. $\frac{- x + 8}{(x^{2} + 3) \sqrt{x^{2} + 2}}$

D. $\frac{- x + 8}{(x^{2} + 2) \sqrt{x^{2} + 2}}$

Xem đáp án

Đáp án D

Câu 4:

Hãy viết số thập phân vô hạn tuần hoàn sau dưới dạng một phân số. α = 34,121212… (chu kỳ 12)

A. $\frac{1126}{33}$

B. $\frac{1263}{34}$

C. $\frac{1311}{35}$

D. $\frac{1411}{37}$

Xem đáp án

Đáp án A

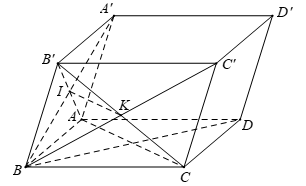
Câu 5:

Cho hình hộp ABCD.A'B'C'D'. Gọi I và K lần lượt là tâm của hình bình hành ABB’A’ và BCC’B’. Khẳng định nào sau đây sai?

A. $\vec{I K} = \frac{1}{2} \vec{A C} = \frac{1}{2} \vec{A' C'}$

B. Bốn điểm I,K,C,A đồng phẳng

C. $\vec{B D} + 2 \vec{I K} = 2 \vec{B C}$

D. Ba vecto $\vec{B D}, \vec{I K}, \vec{B' C'}$ không đồng phẳng

Xem đáp án

Đáp án D

+) A đúng do tính chất đường trung bình trong ΔB'AC và tính chất của hình bình hành ACC'A'.

+) B đúng do IK // AC nên bốn điểm I, K, C, A đồng phẳng.

+) C đúng do việc ta phân tích:

+) D sai do giá của ba vectơ 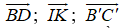đều song song hoặc trùng với mặt phẳng (ABCD). Do đó, theo định nghĩa sự đồng phẳng của các vectơ, ba vectơ trên đồng phẳng.

Câu 6:

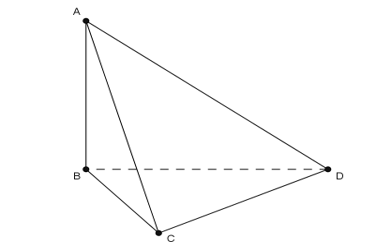
Cho tứ diện ABCD với $A C = \frac{2}{3} A D, ∠ C A B = ∠ D A B = 60 °$ , CD=AD .Gọi là góc giữa AB và CD. Chọn khẳng định đúng?

A. $\cos φ = \frac{1}{4}$

B. $φ = 60 °$

C. $φ = 30 °$

D. $\cos φ = \frac{3}{4}$

Xem đáp án

Đáp án A

- Phương pháp: Sử dụng công thức

- Cách giải:

Câu 7:

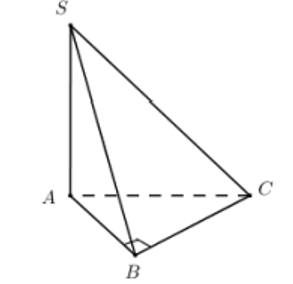
Cho hình chóp S.ABCD có SA ⊥ (ABCD) và ΔABC vuông ở B, AH là đường cao của ΔSAB. Khẳng định nào sau đây sai ?

A. SA ⊥ BC

B. AH ⊥ BC

C. AH ⊥ AC

D. AH ⊥ SC

Xem đáp án

Đáp án C

- Do SA ⊥ (ABC) nên câu A đúng.

- Do BC ⊥ (SAB) nên câu B và D đúng.

- Vậy câu C sai.

Câu 8:

Một chuyển động thẳng xác định bởi phương trình $s = t^{3} - 3 t^{2} + 5 t + 2$ , trong đó t tính bằng giây và s tính bằng mét. Gia tốc của chuyển động khi t= 3 là:

A. 24 $m / s^{2}$

B. 17 $m / s^{2}$

C. 14 $m / s^{2}$

D. 12 $m / s^{2}$

Xem đáp án

Đáp án D

- Ta có gia tốc tức thời của chuyển động tại thời điểm t bằng đạo hàm cấp hai của phương trình chuyển động tại thời điểm t.

- Ta có:

- Suy ra, phương trình gia tốc của chuyển động là:

- Do đó, gia tốc của chuyển động khi t = 3 là: a(3) = 12 $m / s^{2}$

Câu 9:

Cho hàm số y = f(x) có đạo hàm tại $x_{0}$ là $f' (x_{0})$ . Khẳng định nào sau đây sai?

A. $f' (x_{0}) = \lim_{x \to x_{0}} \frac{f (x) - f (x_{0})}{x - x_{0}}$

B. $f' (x_{0}) = \lim_{∆ x \to 0} \frac{f (x_{0} + ∆ x) - f (x_{0})}{∆ x}$

C. $f' (x_{0}) = \lim_{h \to 0} \frac{f (x_{0} + h) - f (x_{0})}{h}$

D. $f' (x_{0}) = \lim_{x \to x_{0}} \frac{f (x + x_{0}) - f (x_{0})}{x - x_{0}}$

Xem đáp án

Đáp án D

- A. Đúng (theo định nghĩa đạo hàm tại một điểm).

- B. Đúng vì:

- C. Đúng vì:

+ Đặt:

Câu 10:

Đạo hàm của hàm số $f (x) = (x^{2} + 1) . (2 x - x^{2})$ tại x = 0 là:

A. -4

B. 4

C. 2

D. 1

Xem đáp án

Đáp án C

- Ta có:

Câu 11:

Cho hình chóp S.ABC có SA ⊥ (ABC) và AB ⊥ BC. Số các mặt của tứ diện S.ABC là tam giác vuông là:

A. 1

B. 3

C. 4

D. 2

Xem đáp án

Đáp án C

- Ta có:

là các tam giác vuông.

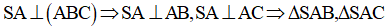
- Ta có:

vuông tại B.

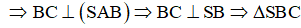
- Vậy hình chóp đã cho có cả 4 mặt đều là tam giác vuông.

Câu 12:

Đạo hàm nào sau đây đúng?

A. $(c o t x)' = - \frac{1}{s i n^{2} x}$

B. (sinx)' = -cosx

C. (cosx)' = sinx

D. $(t a m x)' = - \frac{1}{c o s^{2} x}$

Xem đáp án

Đáp án A

- Phương pháp: Sử dụng các công thức tính đạo hàm của hàm lượng giác.

- Cách giải: Dễ thấy chỉ có đáp án A đúng.

Câu 13:

Phương trình tiếp tuyến của đồ thị hàm số $y = x^{4} + 2 x^{2} - 1$ tại điểm có tung độ tiếp điểm bằng 2 là:

A. y = 8x-6; y = -8x-6

B. y = 8x-6; y = -8x+6

C. y = 8x-8; y = -8x+8

D. y = 40x-57

Xem đáp án

Đáp án A

- Tập xác định: D = R.

- Đạo hàm: $y ’ = 4 x^{3} + 4 x .$

- Tung độ tiếp điểm bằng 2 nên hoành độ tiếp điểm là nghiệm phương trình:

+) Tại M(1; 2) thì y’(1) = 8. Phương trình tiếp tuyến là:

y = 8(x-1) +2 hay y = 8x – 6

+) Tại N(-1; 2) thì y’ (-1) = - 8. Phương trình tiếp tuyến là:

y = - 8(x + 1) + 2 hay y = -8x - 6.

- Vậy có 2 tiếp tuyến thỏa mãn đề bài là: y = 8x – 6 và y = -8x – 6.

Câu 14:

Đạo hàm của hàm số $y = \sqrt{2 + \tan (x + \frac{1}{x})}$ là

A. $y' = \frac{1}{2 \sqrt{2 + \tan (x + \frac{1}{x})}}$

B. $y' = \frac{1 + \tan^{2} (x + \frac{1}{x})}{2 \sqrt{2 + \tan (x + \frac{1}{x})}}$

C. $y' = \frac{1 + \tan^{2} (x + \frac{1}{x})}{2 \sqrt{2 + \tan (x + \frac{1}{x})}} (1 - \frac{1}{x^{2}})$

D. $y' = \frac{1 + \tan^{2} (x + \frac{1}{x})}{2 \sqrt{2 + \tan (x + \frac{1}{x})}} (1 + \frac{1}{x^{2}})$

Xem đáp án

Đáp án C

Câu 15:

Tìm vi phân của các hàm số $y = \sqrt{3 x + 2}$

A. $d y = \frac{3}{\sqrt{3 x + 2}} d x$

B. $d y = \frac{1}{2 \sqrt{3 x + 2}} d x$

C. $d y = \frac{1}{\sqrt{3 x + 2}} d x$

D. $d y = \frac{3}{2 \sqrt{3 x + 2}} d x$

Xem đáp án

Đáp án D

- Ta có :

- Do đó, vi phân của hàm số đã cho là:

Câu 16:

Giới hạn nào sau đây có kết quả bằng 0.

A. $l i m \frac{n^{2} + n}{\sqrt{n^{2} + 10 n}}$

B. $l i m \frac{2 n + 700}{\sqrt{n^{3} + 1}}$

C. $l i m (10 - 3 n)$

D. $l i m \frac{1 - n}{\sqrt{n^{2} + 10 n}}$

Xem đáp án

Đáp án B

Câu 17:

Cho hàm số $y = \frac{x^{2} + 2 x - 3}{x + 2}$ . Đạo hàm của hàm số là:

A. $y' = \frac{x^{2} + 6 x + 7}{{(x + 2)}^{2}}$

B. $y' = \frac{x^{2} + 8 x + 7}{{(x + 2)}^{2}}$

C. $y' = \frac{x^{2} + 4 x + 7}{{(x + 2)}^{2}}$

D. $y' = \frac{x^{2} + 6 x + 5}{{(x + 2)}^{2}}$

Xem đáp án

Chọn C.

Câu 18:

Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết SA = SC và SB = SD. Khẳng định nào sau đây sai?

A. $S O ⊥ (A B C D)$

B. $C D ⊥ (S B D)$

C. $A B ⊥ (S A C)$

D. $C D ⊥ A C$

Xem đáp án

Đáp án B

+) Tam giác SAC cân tại S có SO là trung tuyến

⇒ SO cũng là đường cao ⇒ SO ⊥ AC.

+) Tam giác SBD cân tại S có SO là trung tuyến

⇒ SO cũng là đường cao ⇒ SO ⊥ BD.

- Từ đó suy ra SO ⊥ (ABCD).

→ Do ABCD là hình thoi nên CD không vuông góc với BD. Do đó CD không vuông góc với (SBD).

Câu 19:

Cho hàm số $f (x) = \{\begin{cases} \frac{x^{2} - a}{x - 2} & k h i x \neq 2 \\ 2 b + 1 & k h i x = 2 \end{cases}$ Biết a, b là các giá trị thực để hàm số liên tục tại x = 2. Khi đó a + 2b nhận giá trị bằng:

A. 7

B. 8

C. 11

D. 4

Xem đáp án

Đáp án A

- Phương pháp:

+ Hàm số y = f(x) liên tục tại điểm $x = x_{0}$

- Cách giải:

Ta có:

TH1: a = 4.

- Để hàm số liên tục tại x = 2

TH2: a ≠ 4.

Câu 20:

Cho hàm số g(x) = x.f(x) + x với f(x) là hàm số có đạo hàm trên R. Biết g'(3) = 2, f'(3) = -1 Giá trị của g(3) bằng:

A. -3

B. 3

C. 20

D. 15

Xem đáp án

Đáp án D

- Phương pháp: Sử dụng công thức tính đạo hàm của tích

- Cách giải:

+ Ta có:

Câu 21:

Cho tứ diện ABCD có cạnh AB, BC, BD bằng nhau và vuông góc với nhau từng đôi một. Khẳng định nào sau đây đúng?

A. Góc giữa AC và (BCD) là góc ACB.

B. Góc giữa AD và (ABC) là góc ADB.

C. Góc giữa AC và (ABD) là góc CAB.

D. Góc giữa CD và (ABD) là góc CBD.

Xem đáp án

Đáp án A

- Từ giả thiết ta có

- Do đó

Câu 22:

Tìm giới hạn $C = \lim_{x \to 3} \frac{2 x + 3 - x}{x^{2} - 4 x + 3}$

A. $+ \infty$

B. $- \infty$

C. $- \frac{1}{3}$

D. 1

Xem đáp án

Đáp án C

- Ta có:

Câu 23:

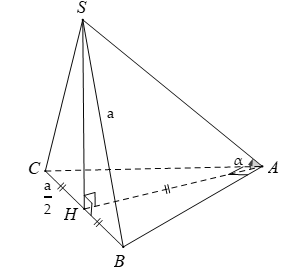
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cạnh huyền BC = a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm BC. Biết SB = a. Tính số đo của góc giữa SA và(ABC).

A. 30°

B. 45°

C. 60°

D. 75°

Xem đáp án

Đáp án C

- Gọi H là trung điểm của BC suy ra:

- Ta có:

Câu 24:

Tìm m để hàm số sau có giới hạn khi x → 1.

$f (x) = \{\begin{cases} \frac{x^{2} + x - 2}{\sqrt{1 - x}} + m x + 1 & k h i x < 1 \\ 3 m x + 2 m - 1 & k h i x \geq 1 \end{cases}$

A. $\frac{2}{3}$

B. $\frac{2}{5}$

C. $\frac{3}{2}$

D. $\frac{1}{2}$

Xem đáp án

Đáp án D

→ Hàm số có giới hạn khi x → 1 khi và chỉ khi:

Câu 25:

Cho hàm số $f (x) = x + \sqrt{x^{2} + 1}$ . Tập các giá trị của x để $2 x . f' (x) - f (x) \geq 0$ là:

A. $(\frac{1}{\sqrt{3}}; + \infty)$

B. $(- \infty; \frac{1}{\sqrt{3}})$

C. $[\frac{2}{\sqrt{3}}; + \infty)$

D. $[\frac{1}{\sqrt{3}}; + \infty)$

Xem đáp án

Đáp án D

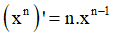
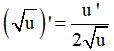
- Phương pháp: Sử dụng công thức và tính f'(x). Từ đó giải bất phương trình.

- Cách giải:

+ Ta có:

+ Theo đề bài ta có: 2x.f'(x) - f(x) ≥ 0.

+ Thử các đáp án:

+ Với 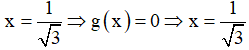thuộc tập nghiệm của BPT.

⇒ Loại đáp án A, B và C.

Câu 26:

Phần II: Tự luận

Tính các giới hạn sau: $C = l i m \frac{3 . 2^{n} - 3^{n}}{2^{n + 1} + 3^{n + 1}}$

Xem đáp án

Ta có:

Câu 27:

Tính các giới hạn sau: $\lim_{x \to - \infty} \frac{\sqrt{9 x^{2} + 1} - 4 x}{3 - 2 x}$

Xem đáp án

Ta có:

Câu 28:

Tính các giới hạn sau: $\lim_{x \to - 2^{+}} \frac{x}{x^{2} + 5 x + 6}$

Xem đáp án

Ta có:

Câu 29:

Chứng minh phương trình sau luôn luôn có nghiệm: $f (x) = (m^{2} - 2 m + 2) x^{3} + 3 x - 3$

Xem đáp án

Xét hàm số $f (x) = (m^{2} - 2 m + 2) x^{3} + 3 x - 3$ . Đây là hàm đa thức nên f(x) liên tục trên R.

- Suy ra: phương trình f(x) = 0 có ít nhất một nghiệm c ∈ (0;1)

Câu 30:

Tìm m để các hàm số $f (x) = \{\begin{cases} \frac{x^{2} + m x + 2 m + 1}{x + 1} & k h i x \geq 0 \\ \frac{2 x + 3 m - 1}{\sqrt{1 - x} + 2} & k h i x < 0 \end{cases}$ có giới hạn khi x → 1

Xem đáp án

Ta có:

- Hàm số có giới hạn khi x → 1 khi và chỉ khi:

Câu 31:

Trên đồ thị của hàm số $y = \frac{1}{x - 1}$ có điểm M sao cho tiếp tuyến tại đó cùng với các trục tọa độ tạo thành một tam giác có diện tích bằng 2. Tìm tọa độ M?

Xem đáp án

Ta có:

- Lấy điểm M(x0;y0) ∈ (C).

- Phương trình tiếp tuyến tại điểm M là:

+ Giao với trục hoành:

+ Giao với trục tung:

- Ta có:

- Theo giả thiết tam giác OAB có diện tích bằng 2 nên:

Câu 32:

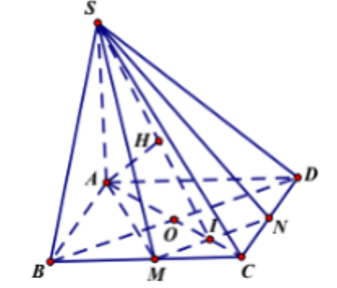
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, SA ⊥ (ABCD) và $S A = a \sqrt{15}$ Gọi M, N lần lượt là trung điểm của BC và CD: Chứng minh (SAC) ⊥ (SBD).

Xem đáp án

Ta có:

Câu 33:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, SA ⊥ (ABCD) và $S A = a \sqrt{15}$ Gọi M, N lần lượt là trung điểm của BC và CD: Tính góc giữa SM và (ABCD).

Xem đáp án

AM là hình chiếu của SM trên (ABCD).

- Xét tam giác vuông ABM ta có:

- Xét tam giác vuông SAM ta có:

Câu 34:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, SA ⊥ (ABCD) và $S A = a \sqrt{15}$ Gọi M, N lần lượt là trung điểm của BC và CD: Tính khoảng cách từ điểm C đến mặt phẳng (SMN)?

Xem đáp án

Gọi I = AC ∩ MN ⇒ I là trung điểm của OC, ta có: