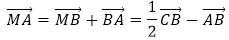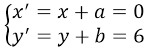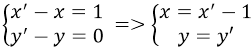15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 11 Bài 1 - 2: Phép biến hình - Phép tịnh tiến (phần 1) (có đáp án)

Câu 1:

Phép biến hình biến điểm M thành điểm M’ thì với mỗi điểm M có:

A. Ít nhất một điểm M’ tương ứng

B. Không quá một điểm M’ tương ứng

C. Vô số điểm M’ tương ứng

D. Duy nhất một điểm M’ tương ứng

quy tắc đặt tương ứng mỗi điểm M của mặt phẳng với một điểm xác định duy nhất M’ của mặt phẳng đó gọi là phép biến hình trong mặt phẳng.

chọn đáp án: D

Câu 2:

Cho tam giác ABC nội tiếp đường trong (O). Qua O kẻ đường thẳng d. Quy tắc nào sau đây là một phép biến hình.

A. Quy tắc biến O thành giao điểm của d với các cạnh tam giác ABC

B. Quy tắc biến O thành giao điểm của d với đường tròn O

C. Quy tắc biến O thành hình chiếu của O trên các cạnh của tam giác ABC

D. Quy tắc biến O thành trực tâm H, biến H thành O và các điểm khác H và O thành chính nó.

Xem đáp án

Các quy tắc A, B, C đều biến O thành nhiều hơn một điểm nên đó không phải là phép biến hình. Quy tắc D biến O thành điểm H duy nhất nên đó là phép biến hình.

Chọn đáp án D

Câu 3:

Cho hình vuông ABCD có M là trung điểm của BC. Phép tịnh tiến theo vecto $\vec{v}$ biến M thành A thì $\vec{v}$ bằng:

A. $\frac{1}{2} \vec{A D} + \vec{D C}$

B. $\vec{A D} + \vec{A C}$

C. $\frac{1}{2} \vec{C B} - \vec{A B}$

D. $\frac{1}{2} \vec{C B} + \vec{A B}$

Xem đáp án

Phép tịnh tiến theo vecto $\vec{v}$ biến M thành A nên $\vec{v} = \vec{M A}$

Chọn đáp án C.

Câu 4:

Cho tam giác ABC có trực tâm H, nội tiếp đường tròn (O), BC cố định, I là trung điểm của BC. Khi A di động trên (O) thì quỹ tích H là đường tròn (O’) là ảnh của O qua phép tịnh tiến theo vecto $\vec{v}$ bằng:

A. $\vec{I H}$

B. $\vec{A O}$

C. $2 \vec{O I}$

D. $1 / 2 \vec{B C}$

Xem đáp án

Gọi A’ là điểm đối xứng với A qua O.

Ta có: BH // A’C suy ra BHCA’ là hình bình hành

Do đó HA’ cắt BC tại trung điểm I của BC.

Mà O là trung điểm của AA’ suy ra OI là đường trung bình của tam giác AHA’

Suy ra $\vec{A H}$ = $2 \vec{O I}$

Do đó vecto $\vec{v} = 2 \vec{O I}$

Chọn đáp án C

Câu 5:

Mặt phẳng tọa độ, phép tịnh tiến theo vecto $\vec{v} (2; - 3)$ biến đường thẳng d: 2x + 3y - 1 = 0 thành đường thẳng d’ có phương trình

A. 3x + 2y - 1 = 0

B. 2x + 3y + 4 = 0

C. 3x + 2y + 1 = 0

D. 2x + 3y + 1 = 0

Xem đáp án

Câu 6:

Tìm mệnh đề đúng trong các mệnh đề sau:

A. Phép tịnh tiến theo vecto $\vec{v}$ biến M thành M’ thì $\vec{v} = \vec{M' M}$

B. Phép tịnh tiến là phép đồng nhất khi vecto tịnh tiến là $\vec{O}$

C. Phép tịnh tiến theo vecto $\vec{v}$ biến M thành M’ và N thành N’ thì tứ giác MNM’N’ là hình bình hành

D. Phép tịnh tiến theo vecto $\vec{v}$ biến đường tròn (O;R) thành đường tròn (O;R)

Xem đáp án

Phương án A. v→ = MM'→ mới đúng nghĩa.

Phương án C. Tứ giác MNN’M’ mới là hình bình hành.

Phương án D. phép tịnh tiến theo vecto v→ chỉ biến đường tròn (O; R) thành đường tròn (O; R) khi vecto tịnh tiến bằng vecto không.

Đáp án B

Câu 7:

Cho tam giác ABC có trọng tâm G, Gọi D, E, F lần lượt là trung điểm của các cạnh BC, CA, AB. Mệnh đề nào sau đây là sai.

A. $T_{1 / 2 \vec{B C}} (F) = E$

B . $T_{\vec{D E}} (B) = F$

C. $T_{2 \vec{D G}} (A) = G$

D. $T_{1 / 2 \vec{G A}} (D) = G$

Xem đáp án

Đáp án C

Ta có: D, E, F lần lượt là trung điểm của các cạnh BC, CA, AB

Do đó: DE, EF, FD là các đường trung bình của tam giác ABC

Suy ra $\{\begin{cases} F E //= \frac{1}{2} B C \\ D E //= \frac{1}{2} A B \\ D F //= \frac{1}{2} A C \end{cases}$

Do đó ta có các phép tịnh tiến như sau: $T_{\frac{1}{2} \vec{B C}} (F) = E$ ; $T_{\vec{D E}} (B) = F$

Lại có G là trọng tâm tam giác ABC nên ta có DG = 1/2GA

$T_{\frac{1}{2} \vec{G A}} (D) = G$ ; $T_{2 \vec{D G}} (G) = A$

Vậy đáp án A, B, D đúng và C sai.

Chọn đáp án C.

Câu 8:

Trong mặt phẳng tọa độ, phép tịnh tiến theo $\vec{v} (1; 2)$ biến điểm M (-1; 4) thành điểm M’ có tọa độ là:

A. M'(0;6)

B. M’(6;0)

C. M’(0;0)

D. M’(6; 6)

Xem đáp án

Thay vào công thức:

Đáp án A

Câu 9:

Trong mặt phẳng tọa độ cho điểm M(-10;1) và điểm M’(3;8). Phép tịnh tiến theo vecto $\vec{v}$ biến M thành M’, thì tọa độ vecto $\vec{v}$ là:

A. $\vec{v} = (- 13; 7)$

B. $\vec{v} (24; - 7)$

C. $\vec{v} (13, 7)$

D. $\vec{v} (- 3; - 7)$

Xem đáp án

Tịnh tiến theo $\vec{v}$ biến điểm M thành điểm M' nên :

$\vec{v} = \vec{M M'} = (13; 7)$

Đáp án C

Câu 10:

Trong mặt phẳng tọa độ, phép tịnh tiến theo vecto $\vec{v} (0; 0)$ biến điểm A(0;2) thành điểm A’ có tọa độ:

A. A’(1;1)

B. A’(1;2)

C. A’(1;3)

D. A’(0;2)

Xem đáp án

Phép tịnh tiến theo vecto không biến mỗi điểm thành chính nó.

Đáp án D

Câu 11:

Trong mặt phẳng tọa độ, phép tịnh tiến theo vecto $\vec{v} (1; 1)$ biến điểm A(0;2) thành A’ và biến điểm B(-2;1) thành B’, khi đó:

A. A’B’ = √5

B. A’B’ = √10

C. A’B’ = √11

D. A’B’ = √12

Xem đáp án

Phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kì .

Phép tịnh tiến theo vecto $\vec{v} (1; 1)$ biến A(0; 2) thành A’(1; 3) và biến B(-2; 1) thành B’(-1; 2)

Do đó; $A' B' = A B = \sqrt{{(- 2 - 0)}^{2} + {(1 - 2)}^{2}} = \sqrt{5}$

Đáp án A

Câu 12:

Trong mặt phẳng tọa độ, phép tịnh tiến theo vecto $\vec{v} (1; 0)$ biến đường thẳng d: x - 1 = 0 thành đường thẳng d’ có phương trình:

A. x - 1 = 0

B. x - 2 = 0

C. x - y - 2 = 0

D. y - 2 = 0

Xem đáp án

Lấy M(x; y) thuộc d; gọi M’(x’; y’) là ảnh của M qua phép tịnh tiến theo vecto $\vec{v} (1; 0)$ thì

Thay vào phương trình d ta được x’ – 2 = 0, hay phương trình d’ là x – 2 = 0.

Đáp án B

Câu 13:

Trong mặt phẳng tọa độ, phép tịnh tiến theo vecto $\vec{v} (3; 1)$ biến đường thẳng d: 12x – 36y + 101 = 0 thành đường thẳng d’ có phương trình:

A. 12x – 36y – 101 = 0

B. 12x + 36y + 101 = 0

C.12x + 36y – 101 = 0

D. 12x – 36 y + 101 = 0.

Xem đáp án

Đường thẳng d có vecto pháp tuyến là: $\vec{n} (12; - 36) = 12 (1; - 3)$

Suy ra, 1 vecto chỉ phương của đường thẳng d là (3; 1)

Vì vecto chỉ phương của d cùng phương với vecto v→ nên phép tịnh tiến theo vecto v→(3;1) biến đường thẳng d thành chính nó.

Đáp án D

Câu 14:

Trong mặt phẳng tọa độ, phép tịnh tiến theo vecto $\vec{v} (- 2; - 1)$ biến parabol (P): y = $x^{2}$ thành parabol (P’) có phương trình:

A. $y = x^{2} + 4 x - 5$

B. $y = x^{2} + 4 x + 4$

C. $y = x^{2} + 4 x + 3$

D. $y = x^{2} - 4 x + 5$

Xem đáp án

Qua phép tịnh tiến theo $\vec{v}$ , biến (P) thành (P')

Lấy M(x; y) thuộc (P); gọi M’(x’; y’) là ảnh của M qua phép tịnh tiến theo vecto $\vec{v} (- 2; - 1)$ thì điểm M' thuộc (P').

Áp dụng biểu thức tọa độ của phép tịnh tiến ta có:

Đáp án C

Câu 15:

Trong mặt phẳng tọa độ, phép tịnh tiến theo vecto $\vec{v} (- 3; - 2)$ biến đường tròn có phương trình (C): $x^{2} + {(y - 1)}^{2} = 1$ thành đường tròn (C’) có phương trình:

A. ${(x - 3)}^{2} + {(y + 1)}^{2} = 1$

B. ${(x + 3)}^{2} + {(y + 1)}^{2} = 1$

C. ${(x + 3)}^{2} + {(y + 1)}^{2} = 4$

D. ${(x - 3)}^{2} + {(y - 1)}^{2} = 4$

Xem đáp án

Đáp án B

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Toán 11 Bài 1 - 2: Phép biến hình - Phép tịnh tiến (có đáp án)

Trắc nghiệm Toán 11 Bài 1 - 2: Phép biến hình - Phép tịnh tiến (phần 1) (có đáp án)

Danh sách câu hỏi

Có thể bạn quan tâm

Các bài thi hot trong chương