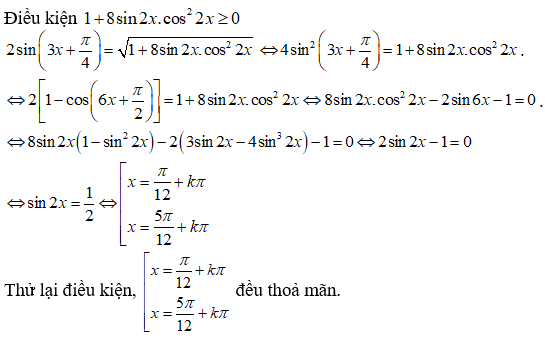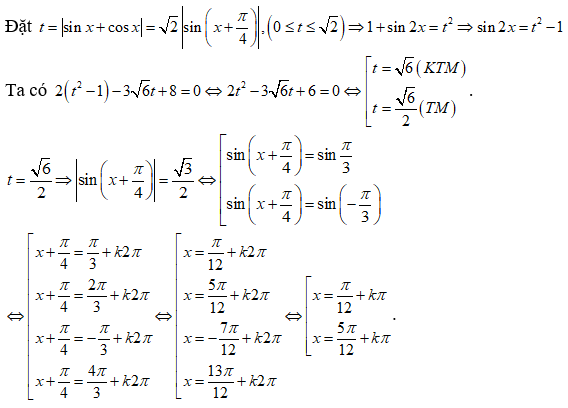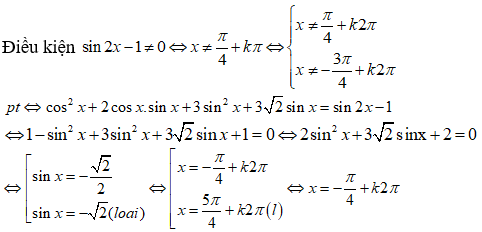20 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 11 Ôn tập chương 1: Hàm số lượng giác nâng cao (phần 3) (có đáp án)

Câu 1:

Số nghiệm thuộc [ $\frac{π}{14}$ ; $\frac{69 π}{10}$ ) của phương trình 2sin3x.(1 – 4sin²x) = 1 là:

A. 40

B. 32

C. 38

D. 46

Xem đáp án

Đáp án C

2sin3x(1 – 4.sin²x) = 1

$\Leftrightarrow 2 \sin 3 x (- 3 + 4 \cos^{2} x) = 1$ (1)

+) TH1: Nếu cosx = 0 thì sin²x = 1

$(1) \Leftrightarrow 2 \sin 3 x (- 3 + 4.0) = 1$

$\Leftrightarrow \sin 3 x = - \frac{1}{6}$

$\Leftrightarrow 3 \sin x - 4 \sin^{3} x = - \frac{1}{6}$

$\Leftrightarrow 3 \sin x - 4 s inx . \sin^{2} x = - \frac{1}{6}$

$\Leftrightarrow 3 \sin x - 4 \sin x = - \frac{1}{6}$

$\Leftrightarrow \sin x = \frac{1}{6}$ (vô lý)

+) TH2: Nếu cosx $\neq 0$ :

$(1) \Leftrightarrow 2 \sin 3 x (- 3 c os x + 4 \cos^{3} x) = c os x$

$\Leftrightarrow 2 \sin 3 x \cos 3 x = c osx$

$\Leftrightarrow \sin 6 x = c os x$

$\Leftrightarrow \sin 6 x = sin (\frac{π}{2} - x)$

$\Leftrightarrow [\begin{array}{l} 6 x = \frac{π}{2} - x + k 2 π \\ 6 x = π - \frac{π}{2} + x + k 2 π \end{array}, k \in ℤ$

$\Leftrightarrow [\begin{array}{l} x = \frac{π}{14} + k \frac{2 π}{7} \\ x = \frac{π}{10} + k \frac{2 π}{5} \end{array}, k \in ℤ$

Vì $x \in [\frac{π}{4}; \frac{69 π}{10})$

$\Rightarrow [\begin{array}{l} \frac{π}{4} \leq \frac{π}{14} + k \frac{2 π}{7} < \frac{69 π}{10} \\ \frac{π}{4} \leq \frac{π}{10} + h \frac{2 π}{5} < \frac{69 π}{10} \end{array}, k, h \in ℤ$

có 21 giá trị k và 17 giá trị h.

Vậy phương trình đã cho có tổng cộng có 21 + 17 = 38 nghiệm.

Câu 2:

Các nghiệm thuộc khoảng (0; $\frac{π}{2}$ ) của phương trình sin³x.cos3x + cos³x.sin3x = $\frac{3}{8}$

A.

B.

C.

D.

Xem đáp án

Đáp án D

Câu 3:

Phương trình $2 \sin (3 x + \frac{π}{4}) = \sqrt{1 + 8 \sin 2 x . \cos^{2} 2 x}$ có nghiệm là:

A.

B.

C.

D.

Xem đáp án

Đáp án B

Câu 4:

Tìm số nghiệm x ∈ (0; π) của phương trình 5cosx + sinx - 3 = $\sqrt{2}$ sin(2x + $\frac{π}{4}$ ) (*)

A: 1

B: 2

C: 3

D: 4

Xem đáp án

Đáp án A

Câu 5:

Tìm m để phương trình 2sin²x – (2m + 1)sinx + m = 0 có nghiệm x ∈ ( $\frac{- π}{2}$ ; 0).

A. -1 < m

B. 1 < m

C. -1 < m < 0

D. 0 < m < 1

Xem đáp án

Đáp án C

Câu 6:

Phương trình $\sin^{3} x + \cos^{3} x + \sin^{3} x . cotx + \cos^{3} x . tanx = \sqrt{2 \sin 2 x}$ có nghiệm là:

A. x = $\frac{π}{8}$ + kπ

B. x = $\frac{π}{4}$ + kπ

C. x = $\frac{π}{4}$ + k2π

D. x = $\frac{3 π}{4}$ + k2π

Xem đáp án

Đáp án B

Kết hợp điều kiện, vậy nghiệm của phương trình đã cho là $x = \frac{π}{4} + k π$

Câu 7:

Phương trình $\frac{\sin^{4} x + \cos^{4} x}{\sin 2 x} = \frac{1}{2} (tanx + cotx)$ có nghiệm là:

A. x = $\frac{π}{2}$ + kπ.

B. x = $\frac{π}{3}$ + k2π

C. x = $\frac{π}{4}$ + k $\frac{π}{2}$

D.Vô nghiệm

Xem đáp án

Đáp án D

Câu 8:

Cho phương trình cos2x.cosx + sinx.cos3x = sin2x.sinx - sin3x.cosx và các họ số thực:

I. x = $\frac{π}{4}$ + kπ, k ∈ Z.

II. x = $\frac{- π}{2}$ + k2π, k ∈ Z.

III. x = $\frac{- π}{14}$ + $\frac{k 2 π}{7}$ , k ∈ Z.

IV. x = $\frac{π}{7}$ + $\frac{k 4 π}{7}$ , k ∈ Z.

Chọn trả lời đúng: Nghiệm của phương trình là:

A. I, II

B. I, III

C. II, III

D. II, IV.

Xem đáp án

Đáp án C

Câu 9:

Tổng các nghiệm thuộc khoảng (0;2018) của phương trình $\sin^{4} \frac{x}{2} + \cos^{4} \frac{x}{2} = 1 - 2 \sin x$ là

A. 207046π

B. 206403π

C. 205761π

D. 204603π

Xem đáp án

Đáp án B

Câu 10:

Tổng 2 nghiệm âm liên tiếp lớn nhất của phương trình 4sin³x – sinx – cosx = 0 bằng:

A.

B.

C.

D. -π

Xem đáp án

Đáp án B

+ Trường hợp 2. $\cos x \neq 0$ . chia cả hai vế cho $\cos^{3} x$ ta được:

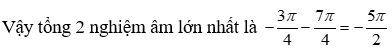
Câu 11:

Cho phương trình sinx.cosx - sinx - cosx + m = 0, trong đó m là tham số thực. Để phương trình có nghiệm, các giá trị thích hợp của m là

A. $- 2 \leq m \leq - \frac{1}{2} - \sqrt{2}$

B. $- \frac{1}{2} - \sqrt{2} \leq m \leq 1$

C. $1 \leq m \leq \frac{1}{2} + \sqrt{2}$

D. $\frac{1}{2} + \sqrt{2} \leq m \leq 2$

Xem đáp án

Đáp án B

Câu 12:

Phương trình 2sin2x - 3 $\sqrt{6}$ |sinx + cosx| + 8 = 0 có nghiệm là

A.

B.

C.

D.

Xem đáp án

Đáp án D

Câu 13:

Tổng các nghiệm của phương trình sinx.cosx + |cosx + sinx| = 1 trên (0; 2π) là:

A. π

B. 2π

C. 3π

D. 4π

Xem đáp án

Đáp án C

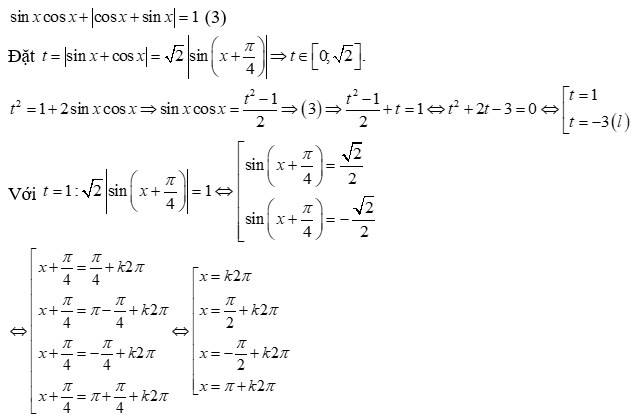
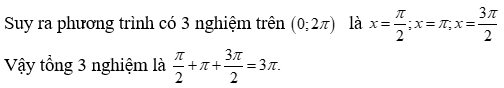
Câu 14:

Có bao nhiêu giá trị nguyên của m để phương trình: sin2x + $\sqrt{2}$ sin(x - $\frac{π}{4}$ ) - m = 0 có nghiệm.

A.3

B.4

C.5

D.6

Xem đáp án

Đáp án B

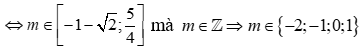
Câu 15:

Giải phương trình $5 (sinx + \frac{\sin 3 x + \cos 3 x}{1 + 2 \sin 2 x}) = \cos 2 x + 3$

A. $x = \pm \frac{π}{3} + k 2 π, k \in ℤ$

B. x = ± $\frac{π}{6}$ + k2π, k ∈ $ℤ$

C. $x = \pm \frac{π}{3} + k π, k \in ℤ$

D. x = ± $\frac{π}{6}$ + kπ, k ∈ $ℤ$

Xem đáp án

Đáp án A

Điều kiện: $\sin 2 x \neq - \frac{1}{2} \Leftrightarrow \{\begin{cases} x \neq - \frac{π}{12} + k π \\ x = \frac{7 π}{12} + k π \end{cases}, k \in ℤ$

$5 (s inx + \frac{3 (s inx - c os x) - 4 (s inx - c os x) (1 + s inx . c os x)}{1 + 2 \sin 2 x}) = \cos 2 x + 3$

$\Leftrightarrow 5 (s inx + \frac{(s inx - c os x) (3 - 4 - 4 s inx . c os x)}{1 + 2 \sin 2 x}) = \cos 2 x + 3$

$\Leftrightarrow 5 (s inx + \frac{(s inx - c os x) (- 1 - 2 s in2x)}{1 + 2 \sin 2 x}) = \cos 2 x + 3$

$\Leftrightarrow 5 (s inx - s inx + c os x) = \cos 2 x + 3$

$\Leftrightarrow 5 c os x = 2 \cos^{2} x - 1 + 3$

$\Leftrightarrow 2 \cos^{2} x - 5 c os x + 2 = 0$

$\Leftrightarrow [\begin{array}{l} cos x = 2 (V L) \\ cosx= \frac{1}{2} \end{array} \Leftrightarrow cosx= \frac{1}{2} \Leftrightarrow x = \pm \frac{π}{3} + k 2 π, k \in ℤ$ (thỏa mãn điều kiện)

Vậy nghiệm của phương trình đã cho là: $x = \pm \frac{π}{3} + k 2 π, k \in ℤ$ .

Câu 16:

Cho phương trình $\frac{1}{2} \cos 4 x + \frac{4 tanx}{1 + \tan^{2} x} = m$ . Để phương trình vô nghiệm, các giá trị của tham số m phải thỏa mãn điều kiện: