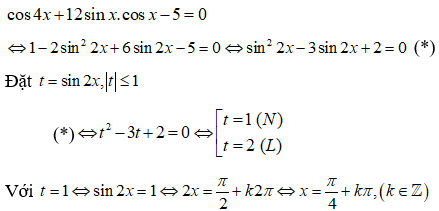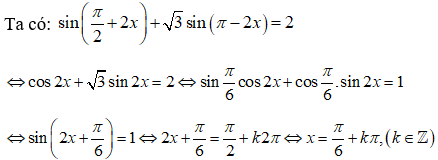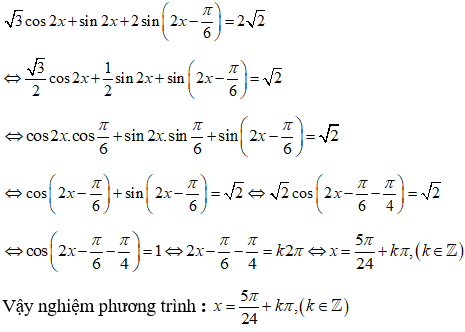20 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 11 Ôn tập chương 1: Hàm số lượng giác nâng cao (phần 4) (có đáp án)

Câu 1:

Giải phương trình: cos⁵x + x² = 0

A.

B.

C.

D.Vô nghiệm

Xem đáp án

Đáp án D

Câu 2:

Tìm nghiệm x ∈ (0; π) của phương trình: 5cosx + sinx - 3 = $\sqrt{2}$ sin(2x + $\frac{π}{4}$ )

A. $x = \frac{π}{3}$

B.

C.

D. Vô nghiệm

Xem đáp án

Đáp án A

Câu 3:

Tìm x ∈ (0; π) thỏa mãn phương trình $4 \sin^{2} \frac{x}{2} - \sqrt{3} \cos 2 x = 1 + 2 \cos^{2} (x - \frac{3 π}{4}) (1)$

A.

B.

C.

D.Tất cả sai

Xem đáp án

Đáp án D

+ Ta có: $k_{1} \in Z; x \in (0; π)$ nên

+ Ta có: $k_{2} \in Z; x \in (0; π)$ nên $k_{2} = 1 \Rightarrow x = \frac{5 π}{6}$

Vậy có tất cả 3 nghiệm thỏa mãn đầu bài

Câu 4:

Giải các phương trình sau: 2cos3x.cosx - 4sin²2x + 1 = 0

A. x = ± $\frac{π}{3}$ + k2π, k ∈ Z

B. x = $\frac{π}{4}$ + kπ, k ∈ Z

C. x = $- \frac{π}{4}$ + k2π, x = $- \frac{π}{6}$ + k2π,k ∈ Z

D. x = ± $\frac{π}{6}$ + kπ

Xem đáp án

Đáp án D

Câu 5:

Giải các phương trình sau:

A. x = ± $\frac{π}{6}$ + k2π, k ∈ Z

B. x = ± $\frac{5 π}{6}$ + k2π, k ∈ Z

C. x = $- \frac{π}{4}$ + k2π, x = $- \frac{π}{6}$ + k2π, k ∈ Z

D. Đáp án khác

Xem đáp án

Đáp án D

Khi đó, phương trình đã cho trở thành: $1 - t^{2} + 4 t = 4$

Câu 6:

Giải phương trình: cos²( $\frac{π}{3}$ + x) + 4cos( $\frac{π}{6}$ – x) = 4

A. x = ± $\frac{π}{6}$ + k2π, k ∈ Z

B. x = ± $\frac{5 π}{6}$ + k2π, k ∈ Z

C. x = $\frac{π}{6}$ + k2π, k ∈ Z

D. Đáp án khác

Xem đáp án

Đáp án C

Câu 7:

Giải phương trình: cos4x + 12sinx.cosx - 5 = 0

A. x = ± $\frac{π}{6}$ + k2π, k ∈ Z

B. x = ± $\frac{5 π}{6}$ + k2π, k ∈ Z

C. x = $\frac{π}{4}$ + k2π, k ∈ Z

D. Đáp án khác

Xem đáp án

Đáp án D

Câu 8:

Giải phương trình: 4cos²(6x – 2) + 16cos²(1 – 3x) = 13

A. x = ± $\frac{π}{6}$ + k2π, k ∈ Z

B. x = ± $\frac{π}{6}$ + k $\frac{2 π}{3}$ , k ∈ Z

C. x = ± $\frac{π}{18}$ + k $\frac{2 π}{3}$ , k ∈ Z

D. Đáp án khác

Xem đáp án

Đáp án D

Câu 9:

Họ nghiệm của phương trình 16(sin⁸x + cos⁸x) = 17cos²2x là:

A. x = $\frac{π}{8}$ + k $\frac{5 π}{4}$

B. x = $\frac{π}{8}$ + k $\frac{7 π}{4}$

C. x = $\frac{π}{8}$ + k $\frac{9 π}{4}$

D. x = $\frac{π}{8}$ + k $\frac{π}{4}$

Xem đáp án

Đáp án D

Nếu ta đặt $t = \sin^{2} 2 x; 0 \leq t \leq 1 \Rightarrow \cos^{2} 2 x = 1 - \sin^{2} 2 x = 1 - t$

Câu 10:

Giải các phương trình sau: sin( $\frac{π}{2}$ + 2x) + $\sqrt{3}$ sin(π - 2x) = 2

A. $x = \pm \frac{π}{6} + k 2 π, k \in ℤ$

B. $x = \pm \frac{5 π}{6} + k 2 π, k \in ℤ$

C. $x = \frac{π}{4} + k 2 π, k \in ℤ$

D. $x = \frac{π}{6} + k π, k \in ℤ$

Xem đáp án

Đáp án D

Câu 11:

Giải phương trình sau: $\sqrt{3} \cos 2 x + \sin 2 x + 2 \sin (2 x - \frac{π}{6}) = 2 \sqrt{2}$

A. x = ± $\frac{5 π}{24}$ + k2π

B. x = $\frac{5 π}{24}$ + k2π

C. x = $\frac{5 π}{24}$ + kπ

D. x = $\frac{π}{6}$ + kπ

Xem đáp án

Đáp án C

Câu 12:

Một họ nghiệm của phương trình: $\sqrt{3} sinx + cosx = \frac{1}{cosx}$ là

A. x = k2π

B. x = $\frac{π}{3}$ + k2π

C. x = $\frac{π}{3}$ + kπ

D. x = $\frac{π}{6}$ + kπ

Xem đáp án

Đáp án C

Câu 13:

Giải phương trình sau: $\frac{1}{cosx} + \frac{1}{\sin x} = \sqrt{2} \sin (x + \frac{π}{4})$

A. x = $\frac{π}{4}$ + kπ

B. x = $- \frac{π}{4}$ + kπ

C. x = $- \frac{π}{4}$ + kπ, kπ

D. x = $\frac{π}{6}$ + kπ

Xem đáp án

Đáp án B

Điều kiện: cosx ≠ 0, sinx ≠ 0

Với điều kiện trên, (*)

⇔ 2(sinx + cosx) = sin2x (cosx + sinx)

⇔ (sinx + cosx)(2 - sin2x) = 0

⇔ sinx + cosx = 0 ⇔ tan x = -1

⇔ x = -π/4 + kπ, k ∈ Z

So với điều kiện, nghiệm của phương trình là: x = -π/4 + kπ, k ∈ Z

Câu 14:

Giải phương trình sau: tanx.sin²x – 2sin²x = 3(cos2x + sinx.cosx)

A. x = ± $\frac{π}{3}$ + kπ

B. x = $- \frac{π}{4}$ + kπ

C. x = $- \frac{π}{4}$ + kπ, kπ

D. Cả A và B đúng

Xem đáp án

Đáp án D

Câu 15:

Giải phương trình sau: 5sinx – 2 = 3(1 – sinx)tan²x

A. x = $\frac{π}{6}$ + k2π, $k \in ℤ$

B. x = $\frac{5 π}{6}$ + kπ, $k \in ℤ$

C. x = $- \frac{5 π}{6}$ + kπ, $k \in ℤ$

D. Đáp án khác.

Xem đáp án

Đáp án D

Điều kiện: cosx $\neq$ 0 (*)

Phương trình $\Leftrightarrow 5 \sin x - 2 = 3. (1 - s inx) \frac{\sin^{2} x}{{cos}^{2} x}$

$\Leftrightarrow 5 \sin x - 2 = 3. (1 - s inx) \frac{\sin^{2} x}{1 - \sin^{2} x}$

$\Leftrightarrow 5 \sin x - 2 = \frac{3 \sin^{2} x}{1 + \sin x}$

$\Leftrightarrow 2 \sin^{2} x + 3 \sin x - 2 = 0$

$\Leftrightarrow [\begin{array}{l} s inx = \frac{1}{2} (T M) \\ s inx = - 2 (L) \end{array}$

Xét $s inx = \frac{1}{2} \Leftrightarrow [\begin{array}{l} x = \frac{π}{6} + k 2 π \\ x = \frac{5 π}{6} + k 2 π \end{array}, k \in ℤ$ (thỏa mãn điều kiện (*))

Vậy nghiệm của phương trình là: $x = \frac{π}{6} + k 2 π$ và $x = \frac{5 π}{6} + k 2 π$ .

Chọn D

Câu 16:

Giải phương trình sau: $\frac{\cos 2 x + 3 \cot 2 x + \sin 4 x}{\cot 2 x - \cos 2 x} = 2$

A. x = $- \frac{π}{12}$ + k2π

B. x = $\frac{5 π}{12}$ + kπ

C. x = $- \frac{π}{12}$ + kπ; x = $- \frac{5 π}{12}$ + kπ

D. Cả A và B đúng

Xem đáp án

Đáp án C

Chú ý: Hai họ nghiệm $x = \frac{- 5 π}{12} + k π$ và $x = \frac{7 π}{12} + k π$ là trùng nhau .

Câu 17:

Giải phương trình sau: $\frac{4 \sin^{2} 2 x + 6 \sin^{2} x - 3 \cos 2 x - 9}{cosx} = 0$

A. x = $- \frac{π}{3}$ + kπ

B. x = $\frac{π}{3}$ + kπ

C. x = $- \frac{π}{12}$ + kπ, $- \frac{5 π}{12}$ kπ

D. Cả A và B đúng

Xem đáp án

Đáp án D

Điều kiện : cosx $\neq 0$

Câu 18:

Giải phương trình sau: $\frac{cosx (cosx + 2 sinx) + 3 sinx (sinx + \sqrt{2})}{\sin 2 x - 1} = 1$

A. x = $- \frac{π}{4}$ + k2π

B. x = $- \frac{3 π}{4}$ + k2π

C. x = ± $\frac{π}{4}$ + kπ

D. Cả A và B đúng

Xem đáp án

Đáp án A

Câu 19:

Giải phương trình sau: $\frac{\sin^{2} 2 x - 2}{\sin^{2} 2 x - 4 \cos^{2} x} = \tan^{2} x$

A. x = $- \frac{π}{4}$ + k2π

B. x = $- \frac{π}{4}$ + k $\frac{π}{2}$

C. x = $- \frac{π}{4}$ + kπ; $\frac{π}{4}$ + kπ

D. Đáp án khác

Xem đáp án

Đáp án D

Câu 20:

Giải phương trình sau: $\frac{1 + \sin 2 x + \cos 2 x}{1 + \cot^{2} x} = \sqrt{2} sinx . \sin 2 x$

A. $x = - \frac{π}{4} + k 2 π, k \in ℤ$

B. $x = - \frac{π}{4} + k \frac{π}{2}, k \in ℤ$

C. $x = \frac{π}{2} + k π, x = \frac{π}{4} + k 2 π, k \in ℤ$

D. $x = \frac{π}{2} + k π, k \in ℤ$

Xem đáp án

Đáp án C

$s inx \neq 0 \Leftrightarrow x \neq k π, k \in ℤ$

Xét phương trình: $\frac{1 + \sin 2 x + \cos 2 x}{1 + \cot^{2} x} = \sqrt{2} s inx . \sin 2 x$

$\Leftrightarrow \sin^{2} x (1 + \sin 2 x + \cos 2 x) = 2 \sqrt{2} s {in}^{2} x . c os x$

$\Leftrightarrow 1 + \sin 2 x + \cos 2 x = 2 \sqrt{2} c os x$

$\Leftrightarrow 1 + \sin 2 x + \cos 2 x = 2 \sqrt{2} c os x$ (do $sinx \neq 0$ )

$\Leftrightarrow 1 + 2 \sin x . c o s x + 2 \cos^{2} x - 1 - 2 \sqrt{2} c os x = 0$

$\Leftrightarrow 2 \sin x . c o s x + 2 \cos^{2} x - 2 \sqrt{2} c os x = 0$

$\Leftrightarrow c os x (2 \sin x + 2 \cos x - 2 \sqrt{2}) = 0$

$\Leftrightarrow [\begin{array}{l} c os x = 0 \\ 2 \sin x + 2 \cos x - 2 \sqrt{2} = 0 \end{array}$

$\Leftrightarrow [\begin{array}{l} c os x = 0 \\ \sin x + \cos x = \sqrt{2} \end{array}$

$\Leftrightarrow [\begin{array}{l} c os x = 0 \\ \sin (x + \frac{π}{4}) = 1 \end{array}$

$\Leftrightarrow [\begin{array}{l} x = \frac{π}{2} + k π \\ x + \frac{π}{4} = \frac{π}{2} + k 2 π \end{array}, k \in ℤ$

$\Leftrightarrow [\begin{array}{l} x = \frac{π}{2} + k π \\ x = \frac{π}{4} + k 2 π \end{array}, k \in ℤ$

Vậy nghiệm của phương trình là: $x = \frac{π}{2} + k π, x = \frac{π}{4} + k 2 π, k \in ℤ$ .

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Toán 11 Ôn tập chương 1: Hàm số lượng giác và phương trình lượng giác (có đáp án)

Trắc nghiệm Toán 11 Ôn tập chương 1: Hàm số lượng giác nâng cao (phần 4) (có đáp án)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương