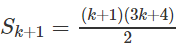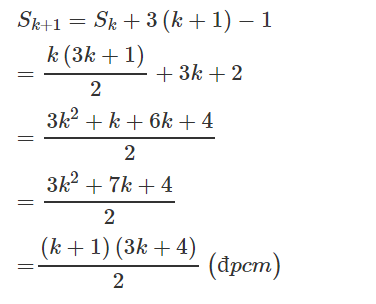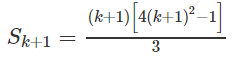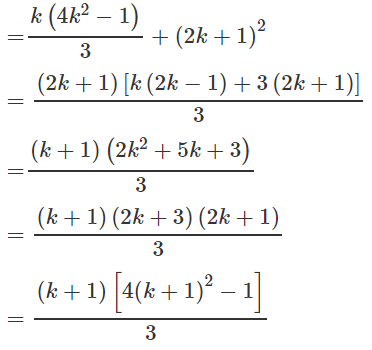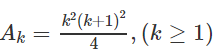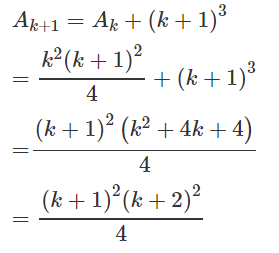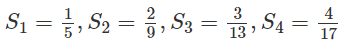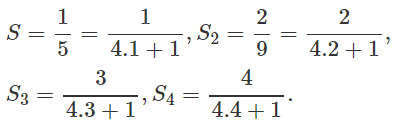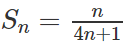6 câu hỏi trắc nghiệm thuộc Giải SBT Bài 1: Phương pháp quy nạp toán học

Giải SBT Toán 11 Chương 3: Dãy số - Cấp số cộng và cấp số nhân

Giải SBT Bài 1: Phương pháp quy nạp toán học

1186 lượt thi
6 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Chứng minh các đẳng thức sau (với n ∈ N∗ )

a) $2 + 5 + 8 + . . . + (3 n - 1) = \frac{n (3 n + 1)}{2};$

b) $3 + 9 + 27 + . . . + 3^{n} = \frac{1}{2} (3^{n + 1} - 3) .$

Xem đáp án

a) Đặt vế trái bằng $S_{n}$ . Kiểm tra với n = 1 hệ thức đúng.

Giả sử đã có 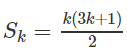với $k \geq 1$ .

Ta phải chứng minh

Thật vậy

b) Đặt vế trái bằng làm tương tự như câu a).

Câu 2:

Chứng minh các đẳng thức sau (với n ∈ N∗ )

a) $1^{2} + 3^{2} + 5^{2} + . . . + {(2 n - 1)}^{2} = \frac{n (4 n^{2} - 1)}{3}$

b) $1^{3} + 2^{3} + 3^{3} + . . . + n^{3} = \frac{n^{2} {(n + 1)}^{2}}{4}$

Xem đáp án

a) Đặt vế trái bằng $S_{n}$

Với n = 1 vế trái chỉ có một số hạng bằng 1, vế phải bằng 1

Giả sử đã có 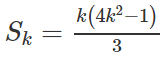với k ≥ 1. Ta phải chứng minh

Thật vậy, ta có

$S_{k + 1} = S_{k} + {[2 (k + 1) - 1]}^{2} = S_{k} + {(2 k + 1)}^{2}$

b) Đặt vế trái bằng An

Dễ thấy với n = 1 hệ thức đúng.

Giả sử đã có

Ta có:

Câu 3:

Chứng minh rằng với mọi n ∈ N∗ ta có

a) $2 n^{3} - 3 n^{2} + n$ chia hết cho 6.

b) $11^{n + 1} + 12^{2 n - 1}$ chia hết cho 133.

Xem đáp án

a) Đặt $B_{n} = 2 n^{3} - 3 n^{2} + n$ tính $B_{1}$

Giả sử đã có $B_{k} = 2 k^{3} - 3 k^{2}$ chia hết cho 6.

Ta phải chứng minh $B_{k + 1} = 2 {(k + 1)}^{3} - 3 {(k + 1)}^{2} + k$ chia hết cho 6.

b) Đặt $A_{n} = 11^{n + 1} + 12^{2 n - 1}$ Dễ thấy $A_{1} = 133$ chia hết cho 133.

Giả sử $A_{k} = 11^{k + 1} + 12^{2 k - 1}$ đã có chia hết cho 133.

Ta có

$A_{k + 1} = 11^{k + 2} + 12^{2 k + 1}$

$= 11 . 11^{k + 1} + 12^{2 k - 1} . 12^{2}$

$= 11 . 11^{k + 1} + 12^{2 k - 1} (11 + 133)$

$= 11 . A_{k} + 133 . 12^{2 k - 1}$

Vì $A_{k}$ chia hết 133 nên $A_{k + 1}$ chia hết 133

Câu 4:

Chứng minh các bất đẳng thức sau (n ∈ N∗)

a) $2^{n + 2} > 2 n + 5$

b) $\sin^{2 n} α + \cos^{2 n} α \leq 1$

Xem đáp án

a) Với $n = 1$ thì $2^{1 + 2} - 8 > 7 = 2.1 + 5$

Giả sử bất đẳng thức đúng với $n = k \geq 1$ tức là $2 k + 2 > 2 k + 5$ (1)

Ta phải chứng minh nó cũng đúng với $n = k + 1$ ,

tức là $2 k + 3 > 2 (k + 1) + 5$ hay $2 k + 3 > 2 k + 7$ (2)

Thật vậy, nhân hai vế của (1) với 2, ta được

$2 k + 3 > 4 k + 10 = 2 k + 7 + 2 k + 3$

Vì $2 k + 3 > 0 nên 2 k + 3 > 2 k + 7$ (đpcm)

b) Với $n = 1$ thì $\sin^{2} α + \cos^{2} α = 1$ bất đẳng thức đúng.

Giả sử đã có $\sin^{2 k} α + \cos^{2 k} α \leq 1$ với $k \geq 1$ , ta phải chứng minh

$\sin^{2 k + 2} α + \cos^{2 k + 2} α \leq 1$

Thật vậy, ta có:

$\sin^{2 k + 2} α + \cos^{2 k + 2} α = \sin^{2 k} α . \sin^{2} α + \cos^{2 k} α . \cos^{2} α \leq \sin^{2 k} α + \cos^{2 k} α \leq 1$

Câu 5:

Với giá trị nào của số tự nhiên n ta có

a) $2^{n} > 2 n + 1;$

b) $2^{n} > n^{2} + 4 n + 5;$

c) $3^{n} > 2^{n} + 7 n$ ?

Xem đáp án

Đây thực chất là bài toán giải bất phương trình trên N*.

Phương pháp : Có thể dùng phép thử, sau đó dự đoán kết quả và chứng minh.

a) Dùng phép thử với n = 1, 2, 3, 4 ta dự đoán: Với thì n ≥ 3 bất đẳng thức đúng. Ta sẽ chứng minh điều đó bằng quy nạp.

Với n = 3 hiển nhiên đã có kết quả đúng, vì $2^{3} = 8 > 2.3 + 1 = 7$

Giả sử bất đẳng thức đúng với n = k tức là $2^{k} > 2 k + 1$ (1)

ta sẽ chứng minh bất đẳng thức đúng với n = k + 1, tức là

$2^{k + 1} > 2 k + 3$ (2)

Thật vậy, nhân hai vế của (1) với 2, ta được

$2^{k + 1} > 4 k + 2 = 2 k + 3 + 2 k - 1 > 2 k + 3$ .

b) Dùng phép thử.

Với n từ 1 đến 6, bất đẳng thức đều không đúng. Tuy nhiên không thể vội vàng kết luận bất phương trình vô nghiệm.

Nếu thử tiếp ta thấy rằng bất phương trình đúng khi n = 7. Ta có thể làm tiếp để đi tới dự đoán: Với thì bất phương trình được nghiệm đúng. Sau đó chứng minh tương tự như câu a).

c) Làm tương tự như câu a) và câu b).

Câu 6:

Cho tổng:

$S_{n} = \frac{1}{1.5} + \frac{1}{5.9} + \frac{1}{9.13} + . . . + \frac{1}{(4 n - 3) (4 n + 1)}$

a) Tính $S_{1}, S_{2}, S_{3}, S_{4}$ ;

b) Dự đoán công thức tính $S_{n}$ và chứng minh bằng phương pháp quy nạp.

Xem đáp án

a) Tính

b) Viết lại

Ta có thể dự đoán

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải SBT Toán 11 Chương 3: Dãy số - Cấp số cộng và cấp số nhân

Giải SBT Bài 1: Phương pháp quy nạp toán học

Danh sách câu hỏi

Bài thi liên quan