50 câu hỏi trắc nghiệm thuộc Tổng hợp đề thi THPTQG môn Toán cực hay, có lời giải chi tiết - đề 4

Câu 1:

Cho hàm số $f (x) = x^{3} - 3 x^{2} + 4$ . Tính $f' (1)$ .

A. -3

B. 0

C. 9

D. 3

Xem đáp án

Đáp án A

Ta có: $f' (x) = 3 x^{2} - 6 x \Rightarrow f' (1) = - 3 .$

Câu 2:

Số mặt phẳng đối xứng của khối lăng trụ tam giác đều là

A. 3

B. 4

C. 6

D. 9

Xem đáp án

Đáp án B

Số mặt phẳng đối xứng cần tìm là 4.

Câu 3:

Trong các dãy số sau, dãy số nào không là cấp số cộng?

A. $\frac{1}{2}; \frac{1}{4}; \frac{1}{6}; \frac{1}{8}; \frac{1}{10}$

B. $\frac{1}{2}; \frac{3}{2}; \frac{5}{2}; \frac{7}{2}; \frac{9}{2}$

C. -8;-6;-4;-2;0

D. 2;2;2;2;2

Xem đáp án

Đáp án A

Dãy số ở phương án B là 1 CSC với công sai d = 1 dãy số ở phương án C là 1 CSC với công sai d = 2 dãy số ở phương án D là 1 CSC với công sai d = 0 dãy số ở phương án A không là 1 CSC, vì $\frac{1}{4} - \frac{1}{2} = - \frac{1}{4} \neq \frac{1}{6} - \frac{1}{4} = - \frac{1}{12} .$

Câu 4:

Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC) và đáy ABC là tam giác cân tại C. Gọi H và K lần lượt là trung điểm của AB và SB. Trong các khẳng định sau, khẳng định nào sai?

A. $C H ⊥ S B$

B. $A K ⊥ B C$

C. $C H ⊥ S A$

D. $C H ⊥ A K$

Xem đáp án

Đáp án B

Vì $∆ A B C$ cân tại C và H là trung điểm của AB nên $C H ⊥ A B .$

Mà $S A ⊥ (A B C) \Rightarrow S A ⊥ C H \Rightarrow C H ⊥ (S A B) \Rightarrow \{\begin{cases} C H ⊥ S A \\ C H ⊥ S B \\ C H ⊥ A K \end{cases} \Rightarrow$

Các khẳng định A,C và D đúng. Khẳng định B sai.

Câu 5:

Hỏi khối đa diện đều loại {4;3} có bao nhiêu mặt?

A. 4

B. 20

C. 6

D. 12

Xem đáp án

Đáp án C

Khối đa diện đều loại {4;3} là hình lập phương => có 6 mặt .

Câu 6:

Khẳng định nào sau đây là khẳng định sai?

A. $\cos x = 0 \Leftrightarrow x = \frac{π}{2} + k 2 π$

B. $\cos x = 1 \Leftrightarrow x = k 2 π$

C. $\cos x = - 1 \Leftrightarrow x = π + k 2 π$

D. $\cos x = 0 \Leftrightarrow x = \frac{π}{2} + k π$

Xem đáp án

Đáp án A

Ta có $\cos x = 0 \Leftrightarrow x = \frac{π}{2} + k π (k \in ℤ)$

Câu 7:

Giải phương trình $\cos 2 x + 5 \sin x - 4 = 0 .$

A. $x = \frac{π}{2} + k π$

B. $x = - \frac{π}{2} + k π$

C. $x = k 2 π$

D. $x = \frac{π}{2} + k 2 π$

Xem đáp án

Đáp án D

Phương trình

$\cos 2 x + 5 \sin x - 4 = 0 \Leftrightarrow 1 - 2 \sin^{2} x + 5 \sin x - 4 = 0 \Leftrightarrow 2 \sin^{2} x - 5 \sin x + 3 = 0 \Leftrightarrow (2 \sin x - 3) (\sin x - 1) = 0 \Leftrightarrow \sin x = 1 \Leftrightarrow x = \frac{π}{2} + k 2 π (k \in ℤ)$

Câu 8:

Cho hàm số $\frac{3 x - 1}{- 2 + x}$ . Khẳng định nào sau đây là đúng?

A. Hàm số luôn nghịch biến trên $ℝ$

B. Hàm số luôn nghịch biến trên từng khoảng xác định

C. Hàm số đồng biến trên các khoảng $(- \infty; 2) v à (2; + \infty)$

D. Hàm số luôn nghịch biến các khoảng $(- \infty; - 2) v à (- 2; + \infty)$

Xem đáp án

Đáp án B

Ta có: $y = \frac{3 x - 1}{x - 2} \Rightarrow y' = \frac{- 5}{{(x - 2)}^{2}} < 0 (\forall x \neq 2)$

Do đó hàm số luôn nghịch biến trên từng khoảng xác định.

Câu 9:

Hàm số $y = \ln (x + 2) + \frac{3}{x + 2}$ đồng biến trên khoảng nào sau đây?

A. $(- \infty; 1)$

B. $(1; + \infty)$

C. $(\frac{1}{2}; 1)$

D. $(- \frac{1}{2}; + \infty)$

Xem đáp án

Đáp án B

Ta có: $D = (- 2; + \infty)$ và $y' = \frac{1}{x + 2} - \frac{3}{{(x + 2)}^{2}} = \frac{x - 1}{{(x + 2)}^{2}} > 0 \Leftrightarrow x > 1$

Do đó hàm số đã cho đồng biến trên khoảng $(1; + \infty)$ .

Câu 10:

Tìm số đường tiệm cận của đồ thị hàm số $y = \frac{2 x - \sqrt{x^{2} - x - 6}}{x^{2} - 1}$

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Đáp án A

Ta có: $D = (- \infty; - 2] \cup [3; + \infty)$ . Khi đó đồ thị hàm số không có tiệm cận đứng vì $x = \pm 1 \notin D .$ Lại có: $\lim_{x \to \infty} y = 0 \Rightarrow$ đồ thị hàm số có 1 tiệm cận ngang là y = 0.

Câu 11:

Phương trình tiếp tuyến của đồ thị hàm số $y = x^{3} - 3 x^{2} + 1$ tại điểm A(3;1)?

A. -9x - 26

B. 9x - 26

C. -9x - 3

D. 9x - 2

Xem đáp án

Đáp án B

Ta có: $y' = 3 x^{2} - 6 x \Rightarrow y' (3) = 9$ Do đó PTTT là: $y = 9 (x - 3) + 1 = 9 x - 26$

Câu 12:

Cho hàm số $y = - 2017 e^{- x} - 3 e^{- 2 x} .$ Mệnh đề nào dưới đây đúng?

A. $y'' + 3 y' + 2 y = - 2017$

B. $y'' + 3 y' + 2 y = - 3$

C. $y'' + 3 y' + 2 y = 0$

D. $y'' + 3 y' + 2 y = 2$

Xem đáp án

Đáp án C

Ta có: $y' = 2017 e^{- x} + 6 e^{- 2 x}; y'' = - 2017 e^{- x} - 12 e^{- 2 x}$

Do đó: $y'' + 3 y' + 2 y = 0 .$

Câu 13:

Tìm số giao điểm của đồ thị (C): $y = x^{3} - 3 x^{2} + 2 x + 2017$ và đường thẳng y = 2017.

A. 3

B. 0

C. 1

D. 2

Xem đáp án

Đáp án A

Phương trình hoành độ giao điểm là: $x^{3} - 3 x^{2} + 2017 = 2017$

$\Leftrightarrow x^{3} - 3 x^{2} + 2 x = 0 \Leftrightarrow x (x - 1) (x - 2) = 0 \Leftrightarrow [\begin{array}{l} x = 0 \\ x = 1 \\ x = 2 \end{array} .$ Vậy có 3 giao điểm.

Câu 14:

Tiếp tuyến với đồ thị hàm số $y = \frac{2 x + 1}{x + 1}$ tại điểm có hoành độ bằng 0 cắt hai trục tọa độ lần lượt tại A và B. Diện tích tam giác OAB bằng

A. 2

B. 3

C. $\frac{1}{2}$

D. $\frac{1}{4}$

Xem đáp án

Đáp án C

Ta có $y' = \frac{1}{{(x + 1)}^{2}} \to y' (0) = 1$ suy ra phương trình tiếp tuyến của (C) là (d): y = x + 1. Đường thẳng cắt Ox tại A(0;1) tại $B (- 1; 0) \Rightarrow S_{∆ O A B} = \frac{1}{2} . O A . O B = \frac{1}{2} .$

Câu 15:

Cho hàm số y = ln x. Khẳng định nào sau đây là khẳng định sai?

A. Hàm số đồng biến trên khoảng $(0; + \infty)$

B. Hàm số có tập giá trị là $(- \infty; + \infty)$

C. Đồ thị hàm số nhận trục Oy làm tiệm cận đứng

D. Hàm số có tập giá trị là $(0; + \infty)$

Xem đáp án

Đáp án D

Hàm số y = ln x có tập giá trị là $ℝ$ .

Câu 16:

Tính đạo hàm của hàm số $y = \log_{2} (2 x + 1)$ .

A. $y' = \frac{2}{2 x + 1}$

B. $y' = \frac{2}{(2 x + 1) \ln 2}$

C. $y' = \frac{1}{(2 x + 1) \ln 2}$

D. $y' = \frac{1}{2 x + 1}$

Xem đáp án

Đáp án B

Ta có $y = \log_{2} (2 x + 1) \to y' = \frac{(2 x + 1)'}{(2 x + 1) . \ln 2} = \frac{2}{(2 x +) . \ln 2} .$

Câu 17:

Tìm tập xác định D của hàm số $y = {(2 - x)}^{1 - \sqrt{3}}$ .

A. $D = (- \infty; + \infty)$

B. $D = (- \infty; 2]$

C. $D = (- \infty; 2)$

D. $D = (2; + \infty)$

Xem đáp án

Đáp án C

Hàm số đã cho xác định khi và chỉ khi $2 - x > 0 \Leftrightarrow x < 2 .$ Vậy $D = (- \infty; 2)$

Câu 18:

Cho a > 0, a $\neq$ 1,x,y là hai số thực khác 0. Khẳng định nào sau đây là khẳng định đúng?

A. $\log_{a} x^{2} = 2 \log_{a} x$

B. $\log_{a} (x y) = \log_{a} x + \log_{a} y$

C. $\log_{a} (x + y) = \log_{a} x + \log_{a} y$

D. $\log_{a} (x y) = \log_{a} |x| + \log_{a} |y|$

Xem đáp án

Đáp án D

Ta có $\log_{a} (x y) = \log_{a} |x| + \log_{a} |y|$

Câu 19:

Có bao nhiêu số tự nhiên có 3 chữ số đôi một khác nhau?

A. 648

B. 1000

C. 729

D. 720

Xem đáp án

Đáp án A

Chữ số hàng trăm, chục, đơn vị lần lượt có 9,9,8 cách chọn.

Do đó có 9.9.8 = 648 số thỏa mãn.

Câu 20:

Một hộp có 5 bi đen, 4 bi trắng. Chọn ngẫu nhiên 2 bi. Xác suất 2 bi được chọn có cùng màu là

A. $\frac{1}{4}$

B. $\frac{1}{9}$

C. $\frac{4}{9}$

D. $\frac{5}{9}$

Xem đáp án

Đáp án D

Xác suất 2 bi được chọn có cùng màu là $\frac{C_{5}^{1} . C_{4}^{1}}{C_{9}^{2}} = \frac{5}{9} .$

Câu 21:

Trong khai triển đa thức $P (x) = {(x + \frac{2}{\sqrt{x}})}^{6} (x > 0) .$ Hệ số của $x^{3}$ là

A. 60

B. 80

C. 160

D. 240

Xem đáp án

Đáp án A

Ta có $P (x) = {(x + 2 x^{- \frac{1}{2}})}^{6} = \sum_{k = 0}^{6} C_{6}^{k} x^{6 - k} . {(2 x^{- \frac{1}{2}})}^{k} = \sum_{k = 0}^{6} C_{6}^{k} . 2^{k} x^{6 - k - \frac{k}{2}}$

Ép cho $6 - k - \frac{k}{2} = 3 \Rightarrow k = 2 \Rightarrow$ hệ số cần tìm là $C_{6}^{2} . 2^{2} = 60 .$

Câu 22:

Tập xác định của hàm số $y = \ln (\frac{x}{\log_{2} x - 2})$ là

A. $D = (3; + \infty)$

B. $D = (- \infty; 0) \cup (3; + \infty)$

C. $D = (4; + \infty)$

D. $D = (- \infty; 0) \cup (4; + \infty)$

Xem đáp án

Đáp án C

Hàm số đã cho xác định khi $\{\begin{cases} x > 0 \\ \frac{x}{\log_{2} x - 2} > 0 \end{cases} \Leftrightarrow x > 4$

Câu 23:

Đường thẳng d: y = x - 5 cắt đồ thị (C): y = $\frac{x + 1}{x - 3}$ tại hai điểm A, B phân biệt. Gọi $d_{1}, d_{2}$ lần lượt là khoảng cách từ A và B đến đường thẳng $∆ : x = 0 .$ Tính $d = d_{1} + d_{2}$

A. d = 9

B. d = -1

C. d = 5

D. d = $5 \sqrt{2}$

Xem đáp án

Đáp án C

Phương trình hoành độ giao điểm : $\frac{x + 1}{x - 3} = x - 5 \Leftrightarrow \{\begin{array}{l} x \neq 3 \\ x^{2} - 9 x + 14 = 0 \end{array} \Leftrightarrow \{\begin{cases} x = 7 \Rightarrow y = 2 \\ x = 2 y \Rightarrow = - 3 \end{cases}$

Do đó $A (7; 2); B (2; - 3) \Rightarrow d = d_{1} + d_{2} = 2 + 3 = 5 .$

Câu 24:

Một hộp chứa 12 viên bi kích thước khác nhau gồm 3 bi màu đỏ, 4 bi màu xanh và 5 bi màu vàng. Chọn ngẫu nhiên cùng một lúc 3 viên bi. Xác suất để 3 bi được chọn có đủ 3 màu là:

A. $\frac{3}{11}$

B. $\frac{3}{55}$

C. $\frac{3}{220}$

D. $\frac{1}{22}$

Xem đáp án

Đáp án A

Lấy ngẫu nhiên 3 viên bi trong 12 viên bi có $C_{12}^{3} = 220$ cách $\Rightarrow n (Ω) = 220$ .

Gọi X là biến cố “3 bi được chọn có đủ 3 màu”

Lấy 1 viên bi màu đỏ trong 3 bi đỏ có 3 cách.

Lấy 1 viên bi màu xanh trong 4 bi xanh có 4 cách.

Lấy 1 viên bi màu vàng trong 5 bi vàng có 5 cách.

Suy ra số kết quả thuận lợi cho biến cố X là $n (X) = 3.4.5 = 60 .$ Vậy $P = \frac{n (X)}{n (Ω)} = \frac{3}{11} .$

Câu 25:

Trong các khẳng định sau, khẳng định nào sai?

A. Một mặt phẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại.

B. Một đường thẳng vuông góc với một mặt phẳng khi nó vuông góc với hai đường thẳng cắt nhau trong mặt phẳng đó.

C. Một đường thẳng a vuông góc với một đường thẳng song song với mặt phẳng thì đường thẳng a sẽ vuông góc với mặt phẳng.

D. Một đường thẳng vuông góc với một trong hai mặt phẳng song song với nhau thì vuông góc với mặt phẳng còn lại.

Xem đáp án

Đáp án C

Các khẳng định A,B,D sai; khẳng định C đúng.

Câu 26:

Tìm giá trị của x,y sao cho dãy số -2 ,x ,6,y theo thứ tự lập thành một cấp số cộng?

A. x = -6, y = -2

B. x = 1, y = 7

C. x = 2, y = 8

D. x = 2, y = 10

Xem đáp án

Đáp án D

Ta có: $\{\begin{cases} 2 x = - 2 + 6 \\ 2.6 = x + y \end{cases} \Leftrightarrow \{\begin{array}{l} x = 2 \\ y = 10 \end{array} .$

Câu 27:

Trong các dãy số $(u_{n})$ được cho bởi các phương án dưới đây, dãy số nào là một cấp số cộng?

A. $u_{n} = \frac{2}{n}$

B. $u_{n} = n^{2}$

C. $u_{n} = n + 2$

D. $u_{n} = 2^{n}$

Xem đáp án

Đáp án C

Xét dãy số $u_{n} = n + 2 .$ Ta có: $u_{n + 1} = n + 1 + 2 - (n + 2) = 1$ không đổi $\Rightarrow u_{n} = n + 2$ là 1 CSC với công sai d = 1.

Câu 28:

Tính giới hạn $I = l i m (\sqrt{n^{2} - 2 n + 3} - n) ?$

A. I = -1

B. I = 0

C. I = $+ \infty$

D. I = 1

Xem đáp án

Đáp án A

Ta có: $I = l i m \frac{\sqrt{n^{2} - 2 n + 3} + n}{- 2 n + 3} = l i m \frac{\sqrt{1 - \frac{2}{n} + \frac{3}{n^{2}} + 1}}{- 2 + \frac{3}{n}} = - 1$

Câu 29:

Cho tứ diện ABCD. Khẳng định nào sau đây là đúng?

A. $\vec{A C} - \vec{C D} = \vec{A D}$

B. $\vec{A B} - \vec{A C} = \vec{D C} - \vec{D B}$

C. $\vec{A B} + \vec{C D} = \vec{A D} + \vec{C B}$

D. $\vec{A B} + \vec{A D} = \vec{B D}$

Xem đáp án

Đáp án C

Xét khẳng định C. Ta có: $\vec{A B} + \vec{C D} = \vec{A D} + \vec{D B} + \vec{C B} + \vec{B D} = \vec{A D} + \vec{C B} \Rightarrow$ đúng.

Câu 30:

Cho hàm số $y = x^{3} - 6 x^{2} + 9 x - 2 (C)$ . Đường thẳng đi qua điểm A(-1;1) và vuông góc với đường thẳng đi qua hai điểm cực trị của (C) là:

A. $y = - \frac{1}{2} x + \frac{3}{2}$

B. $y = \frac{1}{2} x + \frac{3}{2}$

C. y = x + 3

D. x - 2y - 3 = 0

Xem đáp án

Đáp án B

Ta có $y' = 3 x^{2} - 12 x + 9 = 0 \Leftrightarrow [\begin{array}{l} x = 3 \Rightarrow y = - 2 \\ x = 1 \Rightarrow y = 2 \end{array} \Rightarrow \{\begin{array}{l} M (3; - 2) \\ N (1; 2) \end{array} \Rightarrow (M N) : 2 x + y - 4 = 0 .$

Phương trình đường thẳng đi qua điểm A(-1;1) và vuông góc với (MN) là (d): $y = \frac{1}{2} x + \frac{3}{2} .$

Câu 31:

Cho hàm số $f (x) = {(\frac{1}{2})}^{x} . 5^{x^{2}} .$ Khẳng định nào sau đây là đúng:

A. $f (x) > 1 \Leftrightarrow - x \ln 2 + x^{2} \ln 5 > 0$

B. $f (x) > 1 \Leftrightarrow x^{2} + x \log_{2} 5 > 0$

C. $f (x) > 1 \Leftrightarrow x - x^{2} \log_{2} 5 > 0$

D. $f (x) > 1 \Leftrightarrow x^{2} - x \log_{2} 5 > 0$

Xem đáp án

Đáp án A

$f (x) = {(\frac{1}{2})}^{x} . 5^{x^{2}} > 1 \Leftrightarrow \ln [{(\frac{1}{2})}^{x}] + \ln (5^{x^{2}}) = - x \ln 2 + x^{2} \ln 5 > 0 .$

Câu 32:

Cho hai đường thẳng $d_{1}, d_{2}$ song song nhau. Trên $d_{1}$ có 6 điểm tô màu đỏ, trên $d_{2}$ có 4 điểm tô màu xanh. Chọn ngẫu nhiên 3 điểm bất kì trong các điểm trên. Tính xác suất để 3 điểm được chọn lập thành tam giác có 2 đỉnh tô màu đỏ.

A. $\frac{5}{8}$

B. $\frac{5}{32}$

C. $\frac{5}{9}$

D. $\frac{1}{2}$

Xem đáp án

Đáp án D

Lấy 2 đinh tô màu đỏ trong 6 điểm có $C_{6}^{2}$ cách.

Lấy 1 đỉnh tô màu xanh trong 4 điểm có cách.

Suy ra số tam giác tạo thành có 2 đỉnh tô màu đỏ là $C_{6}^{2} . C_{4}^{1} = 60 .$

Vậy xác suất cần tính là $P = \frac{C_{6}^{2} . C_{4}^{1}}{C_{10}^{3}} = \frac{1}{2} .$

Câu 33:

Trên đoạn $[- π; π]$ phương trình $4 \sin x - 3 = 0$ có tất cả bao nhiêu nghiệm?

A. 1

B. 0

C. 2

D. 4

Xem đáp án

Đáp án C

Phương trình đã cho $\Leftrightarrow \sin x = \frac{3}{4} (1)$ Quan sát đường tròn

lượng giác ta thấy có 2 giá trị của $x \in [- π; π]$ thỏa mãn phương trình (1).

Câu 34:

Cho hàm số $y = (x + 1) . e^{3 x}$ . Hệ thức nào sau đây đúng?

A. $y'' + 6 y' + 9 y = 0$

B. $y'' - 6 y' + 9 y = 0$

C. $y'' + 6 y' + 9 y = 10 x e^{x}$

D. $y'' - 6 y' + 9 y = e^{x}$

Xem đáp án

Đáp án B

Ta có $y' = e^{2 x} + 3 (x + 1) e^{3 x} = e^{3 x} (3 x + 4) \Rightarrow y'' = 3 e^{3 x} (3 x + 4) + 3 e^{3 x} = 3 e^{3 x} (3 x + 5) .$

Vậy $y'' - 6 y' + 9 y = 0 .$

Câu 35:

Gọi n là số nguyên dương sao cho $\frac{1}{\log_{3} x} + \frac{1}{\log_{3^{2}} x} + \frac{1}{\log_{3^{3}} x} + . . . + \frac{1}{\log_{3^{n}} x} = \frac{210}{\log_{3} x}$ đúng với mọi x dương. Tìm giá trị của biểu thức P = 2n + 3.

A. P = 32

B. P = 40

C. P = 43

D. P = 23

Xem đáp án

Đáp án C

Ta có: $\frac{1}{\log_{3} x} + \frac{2}{\log_{3} x} + \frac{3}{\log_{3} x} + . . . + \frac{n}{\log_{3} x} = \frac{210}{\log_{3} x}$

$\Leftrightarrow \frac{n (n + 1)}{2 \log_{3} x} = \frac{210}{\log_{3} x} \Leftrightarrow n (n + 1) = 420 \Leftrightarrow n = 20 \Rightarrow P = 2.20 + 3 = 43 .$

Câu 36:

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác đều, SC = SD = $a \sqrt{3}$ . Tính thể tích V của khối chóp S.ABCD theo a

A. $V = \frac{a^{3} \sqrt{2}}{6}$

B. $V = \frac{a^{3}}{6}$

C. $V = a^{3} \sqrt{2}$

D. $V = \frac{a^{3} \sqrt{3}}{3}$

Xem đáp án

Đáp án A

Gọi M, N là trung điểm của $A B, C D \Rightarrow (S M N) ⊥ (A B C D) .$

Tam giác SAB đều $\Rightarrow S M = \frac{a \sqrt{3}}{2};$ tam giác SCD cân $\Rightarrow S N = \frac{a \sqrt{11}}{2}$ .

Kẻ $S H ⊥ M N (H \in M N) \Rightarrow S H ⊥ (A B C D)$

Mặt khác $S_{∆ S M N} = \frac{a^{2} \sqrt{2}}{4} \Rightarrow S H = \frac{2 . S_{∆ S M N}}{M N} = \frac{a \sqrt{2}}{2} .$

Vậy thể tích khối chóp S.ABCD là $V = \frac{1}{3} S H . S_{A B C D} = \frac{1}{3} . \frac{a \sqrt{2}}{2} . a^{2} = \frac{a^{3} \sqrt{2}}{6} .$

Câu 37:

Cho lăng trụ tam giácABC.A'B'C'. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AC, AA', A' C', BC. Khẳng định nào dưới đây là khẳng định đúng?

A. $(M N P) / / (B B' C' C)$

B. $(N Q P) / / (A C' B')$

C. $(M N Q) / / (A' B' C')$

D. $(M P Q) / / (A A' B' B)$

Xem đáp án

Đáp án D

Vì M,Q lần lượt là trung điểm của AC,BC.

Suy ra MQ là đường trung bình của $∆ A B C \Rightarrow M Q / / A B .$

Tương tự, ta cũng có MP // AA'. Vậy $(M P Q) / / (A B B' A') .$

Câu 38:

Cho hàm số $y = m x^{3} - x^{2} - 2 x + 8 m$ có đồ thị $(C_{m})$ . Tìm tất cả các giá trị của tham số m để đồ thị cắt trục hoành tại ba điểm phân biệt.

A. $m \in (- \frac{1}{6}; \frac{1}{2})$

B. $m \in [- \frac{1}{6}; \frac{1}{2}]$

C. $m \in (- \frac{1}{6}; \frac{1}{2}) \ \{0\}$

D. $m \in (- \infty; \frac{1}{2}) \ \{0\}$

Xem đáp án

Đáp án C

Phương trình hoành độ giao điểm là: $m x^{3} - x^{2} 2 x + 8 m = 0$

$\Leftrightarrow m (x + 2) (x^{2} - 2 x + 4) - x (x + 2) = 0 \Leftrightarrow (x + 2) (m x^{2} - 2 m x + 4 m - x) = 0 \Leftrightarrow [\begin{array}{l} x = - 2 \\ g (x) = m x^{2} - (1 + 2 m) x + 4 m = 0 \end{array}$

Để đồ thị $(C_{m})$ cắt trục hoành tại ba điểm phân biệt thì $g (x) = 0$ có 2 nghiệm phân biệt khác -2 $\Leftrightarrow \{\begin{cases} m \neq 0 \\ ∆ = {(1 + 2 m)}^{2} - 16 m^{2} > 0 \\ g (- 2) = 4 m + 2 (1 + 2 m) + 4 m \neq 0 \end{cases} \Leftrightarrow m \in (- \frac{1}{6}; \frac{1}{2}) \ \{0\}$

Câu 39:

Đợt xuất khẩu gạo của Tỉnh Đồng Tháp thường kéo dài 2 tháng (60 ngày). Người ta nhận thấy số lượng gạo xuất khẩu tính theo ngày thứ t được xác định bởi công thức $S (t) = \frac{2}{5} t^{3} - 63 t^{2} + 3240 t - 3100$ (tấn) với $(1 \leq t \leq 60)$ . Hỏi trong 60 ngày đó thì ngày thứ mấy có số lượng xuất khẩu cao nhất?

A. 60

B. 45

C. 30

D. 25

Xem đáp án

Đáp án B

Xét hàm số $S (t) = \frac{2}{5} t^{3} - 63 t^{2} + 3240 t - 3100$ trên đoạn [1;60], có $S' (t) = \frac{6 t^{2}}{5} - 126 t + 3240 .$ Phương trình $S' (t) = 0 \Leftrightarrow \{\begin{array}{l} 1 \leq t \leq 60 \\ 6 t^{2} - 630 t + 16200 = 0 \end{array} \Leftrightarrow [\begin{array}{l} t = 45 \\ t = 60 \end{array} .$

Tính các giá trị $S (45) = 51575; S (60) = 50900 \to \underset{[1; 60]}{m a x} S (t) = S (45) = 51575 .$

Vậy trong 60 ngày đó thì ngày thứ 45 có lượng xuất khẩu cao nhất.

Câu 40:

Hỏi có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số $y = \frac{x^{2} - 3 x + 2}{x^{2} - m x - m + 5}$ không có đường tiệm cận đứng?

A. 9

B. 10

C. 11

D. 8

Xem đáp án

Đáp án B

TH1: Hàm số bị suy biến $\Leftrightarrow m = 3 \Rightarrow y = 1 .$ Khi đó đồ thị hàm số không có TCĐ.

TH2: PT: $x^{2} - m x - m + 5 = 0$ vô nghiệm

$\Leftrightarrow ∆ = m^{2} + 4 m - 20 < 0 \Leftrightarrow - 2 - 2 \sqrt{6} < m < - 2 + 2 \sqrt{6}$

Do đó với $m \in ℤ \Rightarrow m = - 6; - 5; - 4; - 3; - 2; - 1; 0; 1; 2$ (có 9 giá trị của m).

Vậy có 10 giá trị nguyên của m.

Câu 41:

Tính tổng $S = 1 + 2^{2} \log_{\sqrt{2}} 2 + 3^{2} \log_{\sqrt[3]{2}} 2 + 4^{2} \log_{\sqrt[4]{2}} 2 + . . . + 2017^{2} \log_{\sqrt[2017]{2}} 2 .$

A. $S = 1008^{2} . 2017^{2}$

B. $S = 1007^{2} . 2017^{2}$

C. $S = 1009^{2} . 2017^{2}$

D. $S = 1010^{2} . 2017^{2}$

Xem đáp án

Đáp án C

Ta có $\{\begin{cases} \{\begin{cases} 2^{2} . \log_{\sqrt{2}} 2 = 2^{3} . \log_{2} 2 = 2^{3} \\ 3^{2} . \log_{\sqrt{2}} 2 = 3^{3} . \log_{2} 2 = 3^{3} s u y r a S = 1^{3} + 2^{3} + 3^{3} + . . . + 2017^{3} \end{cases} \\ . . . . . . . . \end{cases}$

Mà $x^{3} = {[\frac{x (x + 1)}{2}]}^{2} - {[\frac{x (x - 1)}{2}]}^{2} \Rightarrow S = 1^{3} + 2^{3} + . . . + n^{3} = {[\frac{n (n + 1)}{2}]}^{2} = 1009^{2} . 2017^{2} .$

Câu 42:

Tìm tất cả các giá trị thực của tham số m sao cho hàm số $y = \frac{m}{3} x^{3} + 7 m x^{2} + 14 x - m + 2$ nghịch biến trên nửa khoảng $[1; + \infty)$ ?

A. $(- \infty; - \frac{14}{15})$

B. $(- \infty; - \frac{14}{15}]$

C. $[- 2; - \frac{14}{15}]$

D. $[- \frac{14}{15}; + \infty)$

Xem đáp án

Đáp án B

TH1: Với $m = 0 \to y = 14 x + 2$ suy ra hàm số đồng biến trên

TH2: Với $m \neq 0$ ta có $y' = m x^{2} + 14 m x + 14; \forall x \in ℝ .$

Để hàm số nghịch biến trên $[1; + \infty) \Leftrightarrow y' \leq 0; \forall x \in [1; + \infty) \Leftrightarrow m \leq - \frac{14}{x^{2} + 14 x}; \forall x \in [1; + \infty) (*)$

Xét hàm số $f (x) = - \frac{14}{x^{2} + 14 x}$ tên $[1; + \infty)$ , ta có

$y' = \frac{28 (x + 7)}{x^{2} {(x + 14)}^{2}} > 0 \Rightarrow \underset{[1; + \infty)}{m i n} f (x) = f (1) = - \frac{14}{15} .$

Vậy yêu cầu (*) $\Leftrightarrow m \leq \underset{[1; + \infty)}{m i n} f (x) = - \frac{14}{15} .$

Câu 43:

Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh a; tam giác A’BC đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (ABC) M là trung điểm của cạnh CC’. Tính cosin góc $α$ là góc giữa hai đường thẳng AA’ và BM

A. $\cos α = \frac{2 \sqrt{22}}{11}$

B. $\cos α = \frac{\sqrt{11}}{11}$

C. $\cos α = \frac{\sqrt{33}}{11}$

D. $\cos α = \frac{\sqrt{22}}{11}$

Xem đáp án

Đáp án C

Ta có $\cos α = \cos \hat{(C C'; B M)} = \cos \hat{B M C} .$

Cạnh $A' H = \frac{B C \sqrt{3}}{2} = \frac{a \sqrt{3}}{2}, A H = \frac{A B \sqrt{3}}{2} = \frac{a \sqrt{3}}{2}$

$A A' = \sqrt{A' H^{2} + A H^{2}} = \frac{a \sqrt{6}}{2} \Rightarrow M C = \frac{a \sqrt{6}}{4} .$

Cạnh $B' H = \sqrt{A' B'^{2} + A' H^{2}} = \frac{a \sqrt{7}}{2} .$

Do đó $\cos \hat{B' B H} = \frac{B B'^{2} + B H^{2} - B' H^{2}}{2 B B' . B H} = 0 \Rightarrow B' B ⊥ B H$

$\Rightarrow M C ⊥ B C \Rightarrow c o s \hat{M B C} = \frac{M C}{B M} = \frac{M C}{\sqrt{B C^{2} + M C^{2}}} = \frac{\sqrt{33}}{11} .$

Câu 44:

Gọi M và N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = - 1 + 2 \cos x [(2 - \sqrt{3}) \sin x + c o s x]$ trên $ℝ$ . Biểu thức M + N + 2 có giá trị bằng:

A. 0

B. $4 \sqrt{2 - \sqrt{3}}$

C. 2

D. $\sqrt{2 + \sqrt{3}} + 2$

Xem đáp án

Đáp án C

Ta có $y = - 1 + (2 - \sqrt{3}) . 2 \sin x c o s x + 2 \cos^{2} x = (2 - \sqrt{3}) . \sin 2 x + \cos 2 x .$

Áp dụng bất đẳng thức Bunhicopxki, có

${[(2 - \sqrt{3}) . \sin 2 x + \cos 2 x]}^{2} \leq [{(2 - \sqrt{3})}^{2} + 1^{2}] . (\sin^{2} 2 x + \cos^{2} 2 x) = 8 - 4 \sqrt{3}$

Suy ra $y^{2} \leq 8 - 4 \sqrt{3} \Leftrightarrow \sqrt{8 - 4 \sqrt{3}} \leq y \leq \sqrt{8 - 4 \sqrt{3}} .$ Vậy M + N + 2 = 2.

Câu 45:

Xác định giá trị thực k để hàm số $f (x) = \{\begin{cases} \frac{x^{2016} + x - 2}{\sqrt{2018 x + 1} - \sqrt{x + 2018}}, x \neq 1 \\ k, x = 1 \end{cases}$ liên tục tại x = 1.

A. $k = 1$

B. $k = 2 \sqrt{2019}$

C. $k = \frac{2017 . \sqrt{2018}}{2}$

D. $\frac{20016}{2017} \sqrt{2019}$

Xem đáp án

Đáp án B

Để f(x) liên tục tại x = 1 thì $\lim_{x \to 1} f (x) = f (1)$ . Ta có:

$\lim_{x \to 1} f (x) = l i m \frac{x^{2016} + x - 1}{\sqrt{2018 x + 1} - \sqrt{x + 2018}} = \lim_{x \to 1} \frac{2016 x + 1}{\frac{1009}{\sqrt{2018 x + 1}} - \frac{1}{2 \sqrt{x + 2018}}} = 2 \sqrt{2019}$

Vậy $k = 2 \sqrt{2019} .$

Câu 46:

Một bà mẹ Việt Nam anh hùng được hưởng số tiền là 4 triệu đồng trên một tháng (chuyển vào tài khoản ngân hàng của mẹ vào đầu tháng). Từ tháng 1 năm 2016 mẹ không đi rút tiền mà để lại ngân hàng và được tính lãi suất 1%trên một tháng. Đến đầu tháng 12 năm 2016 mẹ rút toàn bộ số tiền (bao gồm số tiền của tháng 12 và số tiền đã gửi từ tháng 1). Hỏi khi đó mẹ lĩnh về bao nhiêu tiền? (Kết quả làm tròn theo đơn vị nghìn đồng)

A. 50 triệu 730 nghìn đồng

B. 50 triệu 640 nghìn đồng

C. 53 triệu 760 nghìn đồng

D. 48 triệu 480 nghìn đồng

Xem đáp án

Đáp án A

Cuối tháng 1, mẹ nhận được số tiền là $4 . 10^{6} . (1 + 1 %)$ đồng.

Cuối tháng 2, mẹ nhận được số tiền là

$[4 . 10^{6} . (1 + 1 %) + 4 . 10^{6}] . (1 + 1 %) = 4 . 10^{6} . [{(1 + 1 %)}^{2} + (1 + 1 %)]$

Cuối tháng 3, mẹ nhận được số tiền là $4 . 10^{6} . [{(1 + 1 %)}^{3} + {(1 + 1 %)}^{2} + (1 + 1 %)]$ đồng.

... ... ...

Vậy hàng tháng mẹ gửi vào ngân hàng a đồng, lãi suất r% và số tiền thu được sau n tháng là $A = \frac{a}{r} . (1 + r) . [{(1 + r)}^{n} - 1] .$ Suy ra sau 11 tháng, mẹ lĩnh được $A = \frac{4 . 10^{6}}{1 %} . (1 + 1 %) . [{(1 + 1 %)}^{11} - 1] .$

Vì đầu tháng 12 mẹ mới rút tiền nên mẹ được cộng thêm cả tiền lương của tháng 12.

Vậy tổng số tiền mẹ nhận được là $A + 4 . 10^{6} = 50$ triệu 730 nghìn đồng.

Câu 47:

Tam giác ABC vuông tại B, AB = 10, BC = 4 . Gọi M,N lần lượt là trung điểm của AB, AC. Thể tích khối tròn xoay do hình thang vuông BMNC quay một vòng quanh MB là:

A. $\frac{40 π}{3}$

B. $\frac{20 π}{3}$

C. $\frac{120 π}{3}$

D. $\frac{140 π}{3}$

Xem đáp án

Đáp án D

Xét khối nón tròn xoay $(N_{1})$ được tạo thành khi quay tam giác AMN quanh trục $A B \Rightarrow (N_{1})$ có bán kính đáy $r_{1} = M N = 2;$ chiều cao $h_{1} = A M = 5 .$ Suy ra thể tích khối nón $(N_{1})$ là $V_{1} = \frac{1}{3} {πr}_{1}^{2} h = \frac{1}{3} π . 2^{2} . 5 = \frac{20 π}{3} .$

Xét khối nón tròn xoay $(N_{2})$ được tạo thành khi quay tam giác ABC

quanh trục $A B \Rightarrow (N_{2})$ có bán kính đáy $r_{2} = B C = 4;$ chiều cao $h_{2} = A B = 10 .$

Suy ra thể tích khối nón $(N_{2})$ là $V_{2} = \frac{1}{3} {πr}^{2}_{2} h_{2} = \frac{1}{3} π . 4^{2} . 10 = \frac{160 π}{3} .$

Vậy thể tích khối tròn xoay cần tính là $V = V_{1} - V_{2} = \frac{160 π}{3} - \frac{20 π}{3} = \frac{140 π}{3} .$

Câu 48:

Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông ở A, AB = 2a, AC = a, AA' = 4a. M là điểm thuộc cạnh AA' sao cho MA' = 3MA . Tính khoảng cách giữa hai đường chéo nhau BC và C'M

A. $d = \frac{6 a}{7}$

B. $d = \frac{8 a}{7}$

C. $d = \frac{4 a}{3}$

D. $d = \frac{4 a}{7}$

Xem đáp án

Đáp án B

Ta có $B C / / B' C' \Rightarrow B C / / (M B' C') \Rightarrow d (B C; C' M) = d (B; (M B' C')) = d = \frac{3 V_{B . M B' C'}}{S_{M B' C'}}$

Lại có $V_{B . M B' C'} = V_{M . B B' C'} = V_{A' . B B' C'} = \frac{1}{3} B B' . S_{A' B' C'} = \frac{4 a^{3}}{3} .$

Ta có $\{\begin{cases} M B' = \sqrt{A' B'^{2} + A' M^{2}} = a \sqrt{13} \\ M C' = \sqrt{A' C'^{2} + A' M^{2}} = a \sqrt{10} \\ B' C' = \sqrt{A' B'^{2} + A' C'^{2}} = a \sqrt{5} \end{cases}$

Sử dụng công thức Heron $S = \sqrt{p (p - a) (p - b) (p - c)} .$ Trong đó a,b,c là độ dài ba cạnh của một tam giác và $p = \frac{a + b + c}{2}$ . Ta được $S_{M B' C'} = \frac{7 a^{2}}{2} \Rightarrow d = \frac{3 . \frac{4 a^{3}}{3}}{\frac{7 a^{2}}{2}} = \frac{8 a}{7} .$

Câu 49:

Cho dãy số $(u_{n})$ với $u_{1} = \sqrt{2}$ và $u_{n + 1} = \sqrt{2 + u_{n}}, n \geq 1$ . Chọn phát biểu đúng:

A. $(u_{n})$ không bị chặn trên

B. $u_{3} = \sqrt{2 + \sqrt{2 \sqrt{2}}}$

C. $(u_{n})$ là dãy giảm

D. $(u_{n})$ bị chặn

Xem đáp án

Đáp án D

Dễ thấy $u_{n} > 0$ với mọi $n \geq 1$ . Mặt khác thì $u_{n} < 2$ với mọi $n \geq 1$ . Thật vậy: $u_{1} = \sqrt{2} < 2 .$ Giả sử $u_{n} < 2$ với mọi $n \geq 1 \Rightarrow u_{n + 1} = \sqrt{2 + u_{n}} < \sqrt{2 + 2} = 2$ (đúng).Vậy $0 < u_{n} < 2$ với mọi $n \geq 1$ nên dãy này bị chặn.

Câu 50:

Một khối hình trụ có chiều cao bằng 3 lần đường kính của mặt đáy chứa đầy nước. Người ta đặt vào trong khối đó một khối cầu có đường kính bằng đường kính khối trụ và một khối nón có đỉnh tiếp xúc với khối cầu, đáy khối nón trùng với đáy trên của khối trụ (như hình vẽ).

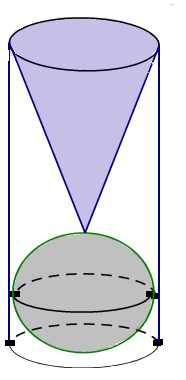
Tính tỉ số thể tích của lượng nước còn lại trong khối trụ và lượng nước của khối trụ ban đầu.

A. $\frac{4}{9}$

B. $\frac{5}{9}$

C. $\frac{2}{3}$

D. $\frac{1}{2}$

Xem đáp án

Đáp án B

Gọi R,h lần lượt là bán kính đáy và chiều cao của khối trụ $\Rightarrow h = 6 R = 6 .$ Thể tích của khối trụ là $V = {πR}^{2} h = π . 1^{2} . 6 = 6 π .$ Khối cầu bên trong khối trụ có bán kính là $R = 1 \Rightarrow V_{C} = \frac{4}{3} π . R^{3} = \frac{4}{3} π .$ Khối nón bên trong khối trụ có bán kính đáy là R = 1 và chiều cao h - 2R = 4. Suy ra thể tích khối nón là $V_{N} = \frac{1}{3} {πR}^{2} h = \frac{1}{3} . π . 1^{2} . 4 = \frac{4}{3} π .$ Do đó, thể tích lượng nước còn lại bên trong khối trụ là $V_{0} = V - (V_{C} + V_{N}) = 6 π - 2 . \frac{4 π}{3} = \frac{10 π}{3} .$ Vậy tỉ số cần tính là $T = \frac{V_{0}}{V} = \frac{10 π}{3} : 6 π = \frac{5}{9} .$

CHỌN BỘ SÁCH BẠN MUỐN XEM

Tổng hợp đề thi THPTQG môn Toán cực hay, có lời giải chi tiết

Tổng hợp đề thi THPTQG môn Toán cực hay, có lời giải chi tiết - đề 4

Danh sách câu hỏi

Bài thi liên quan