Tổng hợp đề thi THPTQG môn Toán cực hay, có lời giải chi tiết - đề 5
-
4480 lượt thi
-
50 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Đồ thị hàm số nào dưới đây không có tiệm cận ngang?
 Xem đáp án
Xem đáp án
Đáp án C.
Ta có Đồ thị hàm số không có tiệm cận ngang.
Câu 2:
Tìm tất cả các giá trị thực của tham số m để hàm số xác định với mọi .
 Xem đáp án
Xem đáp án
Đáp án D.
Hàm số xác định với mọi
Câu 3:
Hàm số nào dưới đây nghịch biến trên tập xác định của nó?
 Xem đáp án
Xem đáp án
Đáp án D.
Ta có Hàm số nghịch biến trên tập xác định.
Câu 5:
Tìm số nghiệm của phương trình
 Xem đáp án
Xem đáp án
Đáp án B
Phương trình đã cho (1).
TH1: Với
TH2: Với (2).
Vì (2) vô nghiệm. Kết hợp 2 trường hợp, suy ra x = 0.
Câu 6:
Cho hàm số y = f(x). Hàm số y = f ' (x) có đồ thị như hình bên.
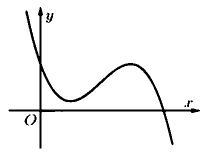
Tìm số điểm cực trị của hàm số y = f(x).
 Xem đáp án
Xem đáp án
Đáp án B.
f ' (x) đổi dấu 1 lần, suy ra hàm số y = f(x) có 1 điểm cực trị.
Câu 7:
Cho hàm số Mệnh đề nào sau đây đúng ?
 Xem đáp án
Xem đáp án
Đáp án C.
Ta có Hàm số không liên tục tại điểm x = 3.
Câu 8:
Cho khối hộp ABCD.A’B’C’D’. Tính tỉ số thể tích của khối hộp đó và khối tứ diện ACB’D’.
 Xem đáp án
Xem đáp án
Đáp án B.
Ta có
Câu 9:
Tính số cách rút ra đồng thời hai con bài từ cỗ bài tú lơ khơ 52 con.
 Xem đáp án
Xem đáp án
Đáp án C.
Số cách rút 2 con bài từ 52 con bài là
Câu 10:
Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số
 Xem đáp án
Xem đáp án
Đáp án D.
Ta có Đồ thị hàm số có tiệm cận ngang là y = 3.
Câu 11:
Biết rằng đồ thị hàm số và đường thẳng y = 9 cắt nhau tại hai điểm phân biệt Tính .
 Xem đáp án
Xem đáp án
Đáp án B.
PT hoành độ giao điểm hai đồ thị là
Câu 12:
Hàm số nào trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây, không có cực trị?
 Xem đáp án
Xem đáp án
Đáp án D.
Ta có:
Câu 13:
Độ giảm huyết áp của một bệnh nhân được xác định bởi công thức trong đó x là liều lượng thuốc tiêm cho bệnh nhân cao huyết áp (x được tính bằng mg). Tìm lượng thuốc để tiêm cho bệnh nhân cao huyết áp để huyết áp giảm nhiều nhất.
 Xem đáp án
Xem đáp án
Đáp án A.
Ta có
Suy ra
Câu 14:
Tính thể tích V của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng a.
 Xem đáp án
Xem đáp án
Đáp án D.
Thể tích khối lăng trụ là
Câu 15:
Trong các dãy số () cho dưới đây, dãy số nào có giới hạn khác 1?
 Xem đáp án
Xem đáp án
Đáp án C.
Dễ thấy
Câu 16:
Đồ thị hàm số và đồ thị hàm số cắt nhau tại hai điểm A và B. Khi đó, độ dài AB là:
 Xem đáp án
Xem đáp án
Đáp án C.
Phương trình hoành độ giao điểm của hai đồ thị là
Câu 18:
Tìm tất cả các đường tiệm cận đứng của đồ thị hàm số
 Xem đáp án
Xem đáp án
Đáp án D.
Ta có
Suy ra Đồ thị hàm số có một tiệm cận đứng là x = 7.
Câu 20:
Cho mặt cầu và mặt phẳng Các giá trị của m để và (S) không có điểm chung là:
 Xem đáp án
Xem đáp án
Đáp án B
Mặt cầu (S) có tâm I(-1;2;3) và bán kính R = 5.
YCBT
Câu 21:
Cho điểm A(-3;2;4) gọi A,B, C lần lượt là hình chiếu của M trên trục Ox, Oy, Oz. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (ABC)
 Xem đáp án
Xem đáp án
Đáp án D.
Ta có A(-3;0;0), B(0;2;0), C(0;0;4)
Câu 22:
Đồ thị hàm số có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang?
 Xem đáp án
Xem đáp án
Đáp án B.
TXĐ:
Ta có: đồ thị hàm số có 1 đường tiệm cận ngang là y = 0.
Mặt khác nên x = 3 là tiệm cận đứng, nên đồ thị hàm số có tiệm cận đứng là x = 2.
Vậy đồ thị hàm số có 3 tiệm cận.
Câu 23:
Cho khối nòn đỉnh O, trục OI. Mặt phẳng trung trực của OI chia khối chóp thành hai phần. Tỉ số thể tích của hai phần là:
 Xem đáp án
Xem đáp án
Đáp án D.
Gọi bán kính của khối nón đỉnh O là r và chiều cao của khối nón là h.
Thể tích của khối nón lớn là
Thể tích của khối nón nhỏ là
Khi đó thể tích phần còn lại là Vậy
Câu 24:
Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ bên. Tất cả các giá trị của tham số m để hàm số y = có ba điểm cực trị là
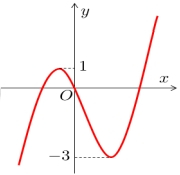
 Xem đáp án
Xem đáp án
Đáp án A.
Ta có (Chú ý: ).
Để hàm số y = g(x) có 3 điểm cực trị có 3 nghiệm phân biệt (1).
Mặt khác, phương trình (2).
Từ (1), (2) suy ra
Câu 26:
Tìm hệ số của trong khai triển nhị thức Newton với x > 0, biết n là số tự nhiên lớn nhất thỏa mãn
 Xem đáp án
Xem đáp án
Đáp án A.
Ta có
Với n = 10, xứt khai triển nhị thức
Hệ số của ứng với Vậy hệ số cần tìm là
Câu 27:
Để đầu tư dự án trồng rau sạch theo công nghệ mới, bác A đã làm hợp đồng xin vay vốn ngân hàng với số tiền 100 triệu đồng với lãi suất x% trên một năm. Điều kiện kèm theo của hợp đồng là số tiền lãi tháng trước sẽ được tính làm vốn để sinh lãi cho tháng sau. Sau hai năm thành công với dự án rau sạch của mình, bác A đã thanh toán hợp đồng ngân hàng số tiền làm tròn là 129 512 000 đồng. Hỏi lãi suất trong hợp đồng giữa bác A và ngân hàng là bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án A.
Ta có
Câu 28:
Trong không gian với hệ trục Oxyz cho điểm A(2;1;3) và đường thẳng có phương trình Mặt phẳng (P) chứa A và d. Viết phương trình mặt cầu tâm O tiếp xúc với mặt phẳng (P).
 Xem đáp án
Xem đáp án
Đáp án D.
đi qua B(1;2;0) có vecto chỉ phương
Với vecto pháp tuyến của (P) là:
Bán kính của mặt cầu cần tìm là
Câu 29:
Một chiếc xô hình nón cụt đựng hóa chất ở phòng thí nghiệm có chiều cao 20cm, đường kính hai đáy lần lượt là 10cm và 20cm. Cô giáo giao cho bạn An sơn mặt ngoài của xô (trừ đáy). Tính diện tích bạn An phải sơn (làm tròn đến hai chữ số sau dấu phẩy).
 Xem đáp án
Xem đáp án
Đáp án D.
Diện tích bạn An cần phải sơn là
Câu 30:
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;1;3), B(0;2;1), C(-2;0;-3). Điểm M thuộc Oz sao cho nhỏ nhất có tọa độ là:
 Xem đáp án
Xem đáp án
Đáp án C.
Do
xảy ra khi a = 1.
Do đó tọa độ điểm M là M(0;0;1).
Câu 32:
Tập giá trị của hàm số trên là:
 Xem đáp án
Xem đáp án
Đáp án A.
Xét hàm số trên có
Suy ra là hàm số nghịch biến trên .
Do đó Vậy tập giá trị cần tìm là
Câu 33:
Cho hàm số (m là tham số thực). Tìm điều kiện của m để hàm số có cực đại và cực tiểu và các điểm cực trị của hàm số nằm bên phải của trục tung
 Xem đáp án
Xem đáp án
Đáp án B.
Ta có
Phương trình (*).
Để hàm số đã cho có 2 điểm cực trị (*) có 2 nghiệm phân biệt
Và các điểm cực trị của hàm số nằm bên phải Oy
Vậy là giá trị cần tìm.
Câu 34:
Tứ diện OABC có OA = OB = OC = 1 và Tìm góc giữa OC và (OAB) để tứ diện có thể tích là
 Xem đáp án
Xem đáp án
Đáp án A.
Gọi H là hình chiếu của C trên mặt phẳng (OAB)
Ta có và
Ta có
Ta có
Mà
Câu 35:
Cho tứ diện S.ABC trên đoạn thẳng SA, SB, SC lần lượt lấy các điểm M, N, P sao cho SM = 5 MA, SN = 2NB và SP = kPC. Kí hiệu là thể tích của khối đa diện T. Biết rằng Tìm k?
 Xem đáp án
Xem đáp án
Đáp án B.
Chọn
Ta có
Câu 36:
Một người nông dân có một tấm cót hình chữ nhật có chiều dài , chiều rộng 1 (m). Người nông dân muốn quây tấm cót thành một chiếc bồ đựng thóc không có đáy, không có nắp đậy, có chiều cao bằng chiều rộng của tấm cót theo các hình dáng sau:
(I). Hình trụ.
(II). Hình lăng trụ tam giác đều.
(III). Hình hộp chữ nhật có đáy là hình chữ nhật có chiều dài gấp đôi chiều rộng.
(IV). Hình hộp chữ nhật có đáy là hình vuông.
Hỏi theo phương án nào trong các phương án trên thì bồ đựng được nhiều thóc nhất (Bỏ qua riềm, khớp nối).
 Xem đáp án
Xem đáp án
Đáp án B.
Hình trụ có chu vi đường tròn đáy là
Hình lăng trụ tam giác đều có chu vi đáy là
Hình hộp chữ nhật đáy là hình chữ nhật có chu vi đáy là
Hình hộp chữ nhật đáy là hình vuông có chu vi đáy là
So sánh theo phương án II thì bồ đựng nhiều thóc nhất.
Câu 38:
Số các giá trị nguyên của tham số để PT có nghiệm là
 Xem đáp án
Xem đáp án
Đáp án C.
Điều kiện: . Dễ thấy x = 0 không là nghiệm của phương trình.
Xét x > 0 chia cả 2 vế của phương trình cho x ta được: (*).
Đặt khi đó phương trình (*)
Vì nên phương trình (*)
Xét hàm số trên , có suy ra
Khi đó, để phương trình m = f(t) có nghiệm
Kết hợp với và suy ra có tất cả 2012 giá trị nguyên m.
Câu 39:
Cho tam giác ABC nội tiếp trong đường tròn tâm O, bán kính R có . Kẻ Quay tam giác ABC quanh trục AC thì tạo thành hình nón xoay có diện tích xung quanh bằng?
 Xem đáp án
Xem đáp án
Đáp án A.
Áp dụng định lý Sin, ta có
Và Xét vuông tại H, ta có
Khi quay quanh trục AC ta được hình nón tròn xoay có bán kính đường tròn đáy r = BH và chiều cao Vậy
Câu 40:
Cho một đa giác đều 20 đỉnh nội tiếp trong đường tròn O. Chọn ngẫu nhiên 4 đỉnh của đa giác đó. Tính xác suất sao cho 4 đỉnh được chọn là 4 đỉnh của một hình chữ nhật
 Xem đáp án
Xem đáp án
Đáp án A.
Có 10 đường kính của đường tròn được nối bởi 2 đỉnh của đa giác đều.
Một hình chữ nhật có 4 đỉnh là đỉnh của đa giác được tạo bởi 2 đường kính nói trên.
Số cách chọn 4 đỉnh của đa giác là Số cách chọn 4 đỉnh của hình chữ nhật là .
Vậy xác suất cần tính là
Câu 41:
Cho hình chóp S.ABCD có đáy là hình vuông; SA = AB = a và Gọi M là trung điểm AD, tính khoảng cách giữa hai đường thẳng SC và BM
Câu 42:
Cho hàm số Tìm giá trị của a để hàm số f(x) liên tục tại điểm x = 0.
 Xem đáp án
Xem đáp án
Đáp án B.
Chú ý giới hạn đặc biệt sau:
và
Do đó
Mà hàm số liên tục tại
Câu 43:
Cho hình chóp S.ABC có độ dài cạnh SA = BC = x, SB = AC = y, SC = AB = z thỏa mãn điều kiện . Tính giá trị lớn nhất của thể tích khối chóp S.ABC.
 Xem đáp án
Xem đáp án
Đáp án C.
Ghép hình chóp vào hình hộp chữ nhật có 3 kích thước là a, b, c.
Ta có
Thể tích khối chóp S.ABCD là
Vậy giá trị lớn nhất của là
Câu 44:
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P) có phương trình với m, n là tham số thực tùy ý. Biết rằng mặt phẳng (P) luôn tiếp xúc với một mặt cầu cố định khi m, n thay đổi. Tìm bán kính mặt cầu đó?
 Xem đáp án
Xem đáp án
Đáp án D.
Gọi I(a,b,c) là tâm mặt cầu cố định đó. Rõ ràng d(I,(P)) = R không đối với mọi .
Với
Với
Rõ ràng không thể xảy ra với mọi suy ra b = 0
Với
Câu 46:
Cho hàm số f(x) liên tục trên thỏa mãn và f(1) = 1. Tính giá trị nhỏ nhất của f(2).
 Xem đáp án
Xem đáp án
Đáp án C.
Ta có
Mặt khác suy ra
Câu 47:
Hàm số y = f(x) có đúng 3 điểm cực trị là -2;-1 và 0. Hỏi hàm số có bao nhiêu điểm cực trị?
 Xem đáp án
Xem đáp án
Đáp án A.
Đặt ta có
Do đó, phương trình
Vậy hàm số đã chốc 3 điểm cực trị là x = 0; x= 1; x = 2.
Câu 48:
Cho khối nón cụt có R, r lần lượt là bán kính hai đáy và h = 3 là chiều cao. Biết thể tích khối nón cụt là tìm giá trị lớn nhất của biểu thức P = R + 2r.
 Xem đáp án
Xem đáp án
Đáp án D.
Khối nón cụt có thể tích là mà (*).
Ta có thay vào (*), ta được
(I).
Vậy phương trình (I) có nghiệm khi và chỉ khi
Vậy giá trị lớn nhất của P là 2.
Câu 49:
Có tất cả bao nhiêu cặp số thực (x,y) thỏa mãn đồng thời các điều kiện và ?
 Xem đáp án
Xem đáp án
Đáp án B.
Với xét từng TH phá giá trị tuyệt đối, ta tìm được nghiệm
Khi đó và
Do đó
Vậy có tất cả hai cặp số thực (x;y) thỏa mãn yêu cầu bài toán.
