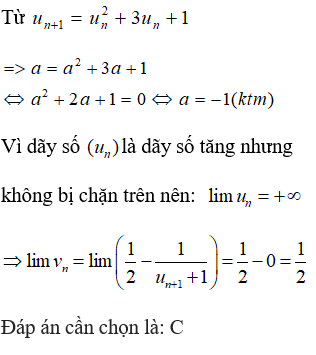10 câu hỏi trắc nghiệm thuộc Trắc nghiệm Giới hạn của dãy số có đáp án (Vận dụng)

Câu 1:

Cho dãy số $(u_{n})$ với $u_{n} = (1 - \frac{1}{2^{2}}) . (1 - \frac{1}{3^{2}}) ... (1 - \frac{1}{n^{2}})$ . Khi đó $\lim (u_{n})$ bằng?

A. $\frac{4}{3}$

B. $\frac{1}{2}$

C. 1

D. 2

Xem đáp án

Câu 2:

Giá trị của $D = \lim (\sqrt{n^{2} + 2 n} - \sqrt[3]{n^{3} + 2 n^{2}})$ bằng:

A. $+ \infty$

B. $- \infty$

C. $\frac{1}{3}$

D. 1

Xem đáp án

Ta có:

$\begin{array}{l} D = \lim (\sqrt{n^{2} + 2 n} - \sqrt[3]{n^{3} + 2 n^{2}}) \\ = \lim (\sqrt{n^{2} + 2 n} - n) - \lim (\sqrt[3]{n^{3} + 2 n^{2}} - n) \\ = \lim \frac{(\sqrt{n^{2} + 2 n} - n) (\sqrt{n^{2} + 2 n} + n)}{(\sqrt{n^{2} + 2 n} + n)} - \lim \frac{[(\sqrt[3]{n^{3} + 2 n^{2}} - n) (\sqrt[3]{{(n^{3} + 2 n^{2})}^{2}} + n \sqrt[3]{n^{3} + 2 n^{2}} + n^{2})]}{\sqrt[3]{{(n^{3} + 2 n^{2})}^{2}} + n \sqrt[3]{n^{3} + 2 n^{2}} + n^{2}} \\ = \lim \frac{n^{2} + 2 n - n^{2}}{\sqrt{n^{2} + 2 n} + n} - \lim \frac{n^{3} + 2 n^{2} - n^{3}}{\sqrt[3]{{(n^{3} + 2 n^{2})}^{2}} + n \sqrt[3]{n^{3} + 2 n^{2}} + n^{2}} \\ = \lim \frac{2 n}{\sqrt{n^{2} + 2 n} + n} - \lim \frac{2 n^{2}}{\sqrt[3]{{(n^{3} + 2 n^{2})}^{2}} + n \sqrt[3]{n^{3} + 2 n^{2}} + n^{2}} \\ = \lim \frac{2}{\sqrt{1 + \frac{2}{n}} + 1} - \lim \frac{2}{{\sqrt[3]{(1 + \frac{2}{n})}}^{2} + \sqrt[3]{1 + \frac{2}{n}} + 1} = \frac{2}{2} - \frac{2}{1 + 1 + 1} = \frac{1}{3} \end{array}$

Đáp án cần chọn là: C

Câu 3:

Giá trị của $D = \lim \frac{\sqrt{n^{2} + 1} - \sqrt[3]{3 n^{3} + 2}}{\sqrt[4]{2 n^{4} + n + 2} - n}$ bằng:

A. $+ \infty$

B. $- \infty$

C. $\frac{1 - \sqrt[3]{3}}{\sqrt[4]{2} - 1}$

D. 1

Xem đáp án

Câu 4:

Cho dãy số $(u_{n})$ với $u_{n} = \frac{1}{1.2} + \frac{1}{2.3} + \frac{1}{3.4} + ... + \frac{1}{n (n + 1)}$ . Khi đó $\lim (u_{n})$ bằng?

A. 0

B. 12

C. 1

D. 2

Xem đáp án

Câu 5:

Tính giới hạn của dãy số $u_{n} = \frac{1}{2 \sqrt{1} + \sqrt{2}} + \frac{1}{3 \sqrt{2} + 2 \sqrt{3}} + ... + \frac{1}{(n + 1) \sqrt{n} + n \sqrt{n + 1}}$

A. $+ \infty$

B. $- \infty$

C. 0

D. 1

Xem đáp án

Ta có:

$\begin{array}{l} \frac{1}{(k + 1) \sqrt{k} + k \sqrt{k + 1}} = \frac{1}{\sqrt{k (k + 1)} (\sqrt{k + 1} + \sqrt{k})} \\ = \frac{\sqrt{k + 1} - \sqrt{k}}{\sqrt{k (k + 1)} (\sqrt{k + 1} + \sqrt{k}) (\sqrt{k + 1} - \sqrt{k})} \\ = \frac{\sqrt{k + 1} - \sqrt{k}}{\sqrt{k (k + 1)} (k + 1 - k)} \\ = \frac{\sqrt{k + 1} - \sqrt{k}}{\sqrt{k} . \sqrt{k + 1}} = \frac{1}{\sqrt{k}} - \frac{1}{\sqrt{k + 1}} \\ \Rightarrow u_{n} = \frac{1}{2 \sqrt{1} + \sqrt{2}} + \frac{1}{3 \sqrt{2} + 2 \sqrt{3}} + ... + \frac{1}{(n + 1) \sqrt{n} + n \sqrt{n + 1}} \\ = \frac{1}{\sqrt{1}} - \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}} - \frac{1}{\sqrt{3}} + ... + \frac{1}{\sqrt{n}} - \frac{1}{\sqrt{n + 1}} \end{array}$

Suy ra $u_{n} = 1 - \frac{1}{\sqrt{n + 1}} \Rightarrow \lim u_{n} = \lim (1 - \frac{1}{\sqrt{n + 1}}) = 1$

do $\lim \frac{1}{\sqrt{n + 1}} = 0$

Đáp án cần chọn là: D

Câu 6:

Giá trị của $K = \lim (\sqrt[3]{n^{3} + n^{2} - 1} - 3 \sqrt{4 n^{2} + n + 1} + 5 n)$ bằng:

A. $+ \infty$

B. $- \infty$

C. $\frac{1}{4}$

D. 1

Xem đáp án

$\begin{array}{l} K = \lim (\sqrt[3]{n^{3} + n^{2} - 1} - 3 \sqrt{4 n^{2} + n + 1} + 5 n) \\ = \lim (\sqrt[3]{n^{3} + n^{2} - 1} - n) - 3 \lim (\sqrt{4 n^{2} + n + 1} - 2 n) \end{array}$

Ta có:

$\begin{array}{l} A = \lim (\sqrt[3]{n^{3} + n^{2} - 1} - n) \\ = \lim \frac{(\sqrt[3]{n^{3} + n^{2} - 1} - n) (\sqrt[3]{{(n^{3} + n^{2} - 1)}^{2}} + \sqrt[3]{n^{3} + n^{2} - 1} + 1)}{(\sqrt[3]{{(n^{3} + n^{2} - 1)}^{2}} + \sqrt[3]{n^{3} + n^{2} - 1} + 1)} \\ = \lim \frac{n^{2} - 1}{(\sqrt[3]{{(n^{3} + n^{2} - 1)}^{2}} + \sqrt[3]{n^{3} + n^{2} - 1} + 1)} \\ = \lim \frac{1 - \frac{1}{n^{2}}}{\sqrt[3]{{(1 + \frac{1}{n} - \frac{1}{n^{3}})}^{2} + \sqrt[3]{\frac{1}{n^{3}} + \frac{1}{n^{4}} - \frac{1}{n^{6}}} + \frac{1}{n^{2}}}} \\ = \frac{1}{1 + 0 + 0} = 1 \end{array}$

$\begin{array}{l} B = \lim (\sqrt{4 n^{2} + n - 1} - 2 n) \\ = \lim \frac{(\sqrt{4 n^{2} + n - 1} - 2 n) (\sqrt{4 n^{2} + n - 1} + 2 n)}{(\sqrt{4 n^{2} + n - 1} + 2 n)} \\ = \lim \frac{4 n^{2} + n - 1 - 4 n^{2}}{(\sqrt{4 n^{2} + n - 1} + 2 n)} \end{array}$

$\begin{array}{l} = \lim \frac{n - 1}{(\sqrt{4 n^{2} + n - 1} + 2 n)} \\ = \lim \frac{1 - \frac{1}{n}}{\sqrt{4 + \frac{1}{n} - \frac{1}{n^{2}}} + 2} \\ = \frac{1}{\sqrt{4} + 2} = \frac{1}{4} \\ \Rightarrow K = A - 3 B = 1 - \frac{3}{4} = \frac{1}{4} \end{array}$

Đáp án cần chọn là: C

Câu 7:

Cho dãy số $(u_{n})$ xác định bởi $\{\begin{cases} u_{1} = 2 \\ u_{n + 1} = \frac{u_{n} + 1}{2}, (n \geq 1) \end{cases}$ . Khi đó mệnh đề nào sau đây là đúng?

A. Dãy $(u_{n})$ là dãy giảm tới 1 khi n→ $+ \infty$

B. Dãy $(u_{n})$ là dãy tăng tới 1 khi n→ $+ \infty$

C. Không tồn tại giới hạn của dãy $(u_{n})$ .

D. Cả 3 đáp án trên đều sai

Xem đáp án

$\begin{array}{l} u_{2} = \frac{2 + 1}{2} = \frac{3}{2} = \frac{2^{1} + 1}{2^{1}} \\ u_{3} = \frac{\frac{3}{2} + 1}{2} = \frac{5}{4} = \frac{2^{2} + 1}{2^{2}} \\ u_{4} = \frac{\frac{5}{4} + 1}{2} = \frac{9}{8} = \frac{2^{3} + 1}{2^{3}} \end{array}$

Chứng minh bằng quy nạp: $u_{n + 1} = \frac{2^{n} + 1}{2^{n}}, \forall n = 1, 2, ... (*);$

* Với $n = 1; u_{2} = \frac{u_{1} + 1}{2} = \frac{2 + 1}{2} = \frac{2^{1} + 1}{2^{1}} : (*)$ đúng

* Giả sử (*) đúng với $n = k \geq 1$ , tức là $u_{k} = \frac{2^{k} + 1}{2^{k}}$ ta chứng minh (*) đúng với $n = k + 1$ , tức là cần chứng minh $u_{k + 1} = \frac{2^{k + 1} + 1}{2^{k + 1}}$

Ta có :

$u_{k + 1} = \frac{u_{k} + 1}{2} = \frac{\frac{2^{k} + 1}{2^{k}} + 1}{2} = \frac{\frac{2^{k} + 1 + 2^{k}}{2^{k}}}{2} = \frac{{2.2}^{k} + 1}{{2.2}^{k}} = \frac{2^{k + 1} + 1}{2^{k + 1}}$

Theo nguyên lý quy nạp, ta chứng minh được (*).

Như vậy, công thức tổng quát của dãy $(u_{n})$ là:

$u_{n} = \frac{2^{n - 1} + 1}{2^{n - 1}} = 1 + \frac{1}{2^{n - 1}}, \forall n = 1; 2; ... (*)$

Từ (*) ta có $u_{n + 1} - u_{n} = 1 + \frac{1}{2^{n}} - (1 + \frac{1}{2^{n - 1}}) = \frac{1}{2^{n}} - \frac{1}{2^{n - 1}} < 0 \forall n = 1, 2, ...$

⇒ $(u_{n})$ là dãy giảm và $\lim u_{n} = \lim (1 + \frac{1}{2^{n - 1}}) = 1$

⇒ $(u_{n})$ là dãy giảm tới 1 khi n→+∞

Đáp án cần chọn là: A

Câu 8:

Tính giới hạn của dãy số $u_{n} = q + 2 q^{2} + ... + n q^{n}$ với $|q| < 1$

A. $+ \infty$

B. $- \infty$

C. $\frac{q}{{(1 - q)}^{2}}$

D. $\frac{q}{{(1 + q)}^{2}}$

Xem đáp án

Câu 9:

Cho dãy số $(u_{n})$ xác định bởi $\{\begin{cases} u_{1} = 1 \\ u_{n + 1} = \sqrt{u_{n} (u_{n} + 1) (u_{n} + 2) (u_{n} + 3) + 1}, (n \geq 1) \end{cases}$ . Đặt $v_{n} = \sum_{i = 2}^{n} \frac{1}{u_{i} + 2}$ . Tính $\lim (v_{n})$ bằng?