12 câu hỏi trắc nghiệm thuộc Trắc nghiệm Hoán vị chỉnh hợp tổ hợp có đáp án

Câu 1:

Số các hoán vị của 10 phần tử là:

A. $10^{2}$

B. 10!

C. 11

D. 10.9

Xem đáp án

Câu 2:

Số chỉnh hợp chập k của n phần tử là:

A. $A_{n}^{k} = \frac{n!}{(n - k)!}$

B. $A_{n}^{k} = \frac{n!}{k!}$

C. $A_{n}^{k} = \frac{(n - k)!}{n!}$

D. $A_{n}^{k} = \frac{k!}{n!}$

Xem đáp án

Số chỉnh hợp chập kk của nn phần tử là:

$A_{n}^{k} = \frac{n!}{(n - k)!}$ = n(n−1)(n−2)...(n−k+1)

Đáp án cần chọn là: A

Chú ý

Một số em có thể sẽ chọn nhầm đáp án B

vì nhớ nhầm công thức tính số chỉnh hợp

chập k của n phần tử.

Câu 3:

Số cách chọn một ban chấp hành gồm một trưởng ban, một phó ban, một thư kí và một thủ quỹ được chọn từ 16 thành viên là:

A. 4

B. $\frac{16!}{4}$

C. $\frac{16!}{12! .4!}$

D. $\frac{16!}{12!}$

Xem đáp án

Đáp án:

Chọn 4 trong 16 thành viên để bầu ban

chấp hành (có phân biệt thứ tự) có

$A_{16}^{4} = \frac{16!}{12!}$

Đáp án cần chọn là: D

Câu 4:

Số các số có 4 chữ số đôi một khác nhau được tạo thành từ các chữ số 2,4,6,7,8,9 là:

A. $A_{4}^{6}$

B. $C_{6}^{4}$

C. $A_{6}^{4}$

D. $C_{4}^{6}$

Xem đáp án

Mỗi số thỏa mãn bài toán và một

chỉnh hợp chập 4 của 6 phần tử.

Số các số là: $A_{6}^{4} = 360$ số.

Đáp án cần chọn là: C

Chú ý

Một số em có thể sẽ chọn nhầm đáp

án A vì nhớ nhầm công thức tính số

chỉnh hợp chập k của n phần tử.

Câu 5:

Giá trị của n∈N bằng bao nhiêu, biết $\frac{5}{C_{5}^{n}} - \frac{2}{C_{6}^{n}} = \frac{14}{C_{7}^{n}}$ .

A. n=2 hoặc n=4.

B. n=5.

C. n=4.

D. n=3.

Xem đáp án

Câu 6:

Tích các giá trị x nguyên thỏa mãn bất phương trình $\frac{1}{2} A_{2 x}^{2} - A_{x}^{2} \leq \frac{6}{x} C_{x}^{3} + 10$ là:

A. 10

B. 15

C. 12

D. -8

Xem đáp án

ĐK: $\{\begin{matrix} 2 x \geq 2 \\ x \geq 2 \\ x \geq 3 \end{matrix} \Leftrightarrow x \geq 3$ , x∈N

$\begin{array}{l} \frac{1}{2} A_{2 x}^{2} - A_{x}^{2} \leq \frac{6}{x} C_{x}^{3} + 10 \\ \Leftrightarrow \frac{1}{2} \frac{(2 x)!}{(2 x - 2)!} - \frac{x!}{(x - 2)!} \leq \frac{6}{x} \frac{x!}{3! (x - 3)!} + 10 \\ \Leftrightarrow \frac{(2 x - 1) 2 x}{2} - x (x - 1) \leq (x - 1) (x - 2) + 10 \\ \Leftrightarrow 2 x^{2} - x - x^{2} + x - x^{2} + 3 x - 2 - 10 \leq 0 \\ \Leftrightarrow 3 x - 12 \leq 0 \\ \Leftrightarrow x \leq 4 \end{array}$

Kết hợp điều kiện ta có $3 \leq x \leq 4$

Mà $x \in Z$ $\Rightarrow [\begin{matrix} x_{1} = 3 \\ x_{2} = 4 \end{matrix} \Rightarrow x_{1} . x_{2} = 3.4 = 12$

Đáp án cần chọn là: C

Câu 7:

Biết n là số nguyên dương thỏa mãn $3 C_{n + 1}^{3} - 3 A_{n}^{2} = 52 (n - 1)$ .Giá trị của n bằng:

A. n=13.

B. n=16.

C. n=15.

D. n=14.

Xem đáp án

* PP tự luận:

PT $\Leftrightarrow 3. \frac{(n + 1)!}{(n - 2)! 3!} - 3. \frac{n!}{(n - 2)!} = 52 (n - 1)$

,(n∈N,n≥2)

$\begin{array}{l} \Leftrightarrow \frac{(n - 1) n (n + 1)}{2} - 3 (n - 1) n = 52 (n - 1) \\ \Leftrightarrow n (n + 1) - 6 n = 104 \Leftrightarrow n^{2} - 5 n - 104 = 0 \\ \Leftrightarrow [\begin{matrix} n = 13 (T M) \\ n = - 8 (L) \end{matrix} \end{array}$

$\Leftrightarrow n = 13$

Đáp án cần chọn là: A

Chú ý

* PP trắc nghiệm:

+ Nhập vào máy tính

$3 C_{n + 1}^{3} - 3 A_{n}^{2} - 52 (n - 1) = 0$

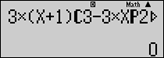
+ Tính (CALC) lần lượt với X=13 (thoả);

với X=16 (không thoả),

với X=15 (không thoả),

với X=14 (không thoả).

Câu 8:

Giá trị của biểu thức $A_{n + k}^{n + 1} + A_{n + k}^{n + 2}$ bằng biểu thức nào sau đây?

A. $k^{2} A_{n + k}^{n}$

B. $k A_{n + k + 1}^{n + 2}$

C. $A_{n + k + 1}^{n + 1}$

D. $A_{n}^{k}$

Xem đáp án

$\begin{array}{l} A_{n + k}^{n + 1} + A_{n + k}^{n + 2} = \frac{(n + k)!}{(k - 1)!} + \frac{(n + k)!}{(k - 2)!} \\ = \frac{(n + k)!}{(k - 1)!} + \frac{(n + k)! . (k - 1)}{(k - 2)! . (k - 1)} \\ = \frac{(n + k)! (1 + k - 1)}{(k - 1)!} = k . \frac{(n + k)!}{(k - 1)!} \\ = k^{2} \frac{(n + k)!}{k!} = k^{2} A_{n + k}^{n} \end{array}$

Đáp án cần chọn là: A

Câu 9:

Giải hệ phương trình $\{\begin{matrix} 2 A_{x}^{y} + 5 C_{x}^{y} = 90 \\ 5 A_{x}^{y} - 2 C_{x}^{y} = 80 \end{matrix}$ ta được nghiệm (x;y) thì x.y bằng :

A. 5

B. 7

C. 10

D. -2

Xem đáp án

ĐK: x≥y≥0,x,y∈N

Đặt a= $A_{x}^{y}$ ;y= $C_{x}^{y}$ ta được

$\{\begin{matrix} 2 x + 5 y = 90 \\ 5 x - 2 y = 80 \end{matrix} \Leftrightarrow \{\begin{matrix} a = 20 \\ b = 10 \end{matrix} \Leftrightarrow \{\begin{matrix} A_{x}^{y} = 20 \\ C_{x}^{y} = 10 \end{matrix}$

Ta có: $\begin{array}{l} C_{x}^{y} = \frac{A_{x}^{y}}{y!} \Leftrightarrow 10 = \frac{20}{y!} \\ \Leftrightarrow y! = 2 \Leftrightarrow y = 2 \end{array}$

$\begin{array}{l} \Rightarrow A_{x}^{2} = 20 \Leftrightarrow \frac{x!}{(x - 2)!} = 20 \\ \Leftrightarrow x (x - 1) = 20 \\ \Leftrightarrow x^{2} - x - 20 = 0 \Leftrightarrow [\begin{matrix} x = 5 (t m) \\ x = - 4 (k t m) \end{matrix} \\ \Rightarrow x y = 5.2 = 10 \end{array}$

Đáp án cần chọn là: C

Câu 10:

Số nghiệm của hệ phương trình $\{\begin{matrix} C_{y}^{x} : C_{y + 2}^{x} = \frac{1}{3} \\ C_{y}^{x} : A_{y}^{x} = \frac{1}{24} \end{matrix}$ là:

A. 2

B. 1

C. 0

D. 3

Xem đáp án

ĐK: $\{\begin{matrix} 0 \leq x \leq y \\ 0 \leq x \leq y + 2 \end{matrix} \Leftrightarrow 0 \leq x \leq y$ (x,y∈N)

$\begin{array}{l} \{\begin{matrix} C_{y}^{x} : C_{y + 2}^{x} = \frac{1}{3} \\ C_{y}^{x} : A_{y}^{x} = \frac{1}{24} \end{matrix} \Leftrightarrow \{\begin{matrix} \frac{y!}{x! (y - x)!} . \frac{x! (y + 2 - x)!}{(y + 2)!} = \frac{1}{3} \\ \frac{y!}{x! (y - x)!} . \frac{(y - x)!}{y!} = \frac{1}{24} \end{matrix} \\ \Leftrightarrow \{\begin{matrix} \frac{(y - x + 1) (y - x + 2)}{(y + 1) (y + 2)} = \frac{1}{3} \\ \frac{1}{x!} = \frac{1}{24} \end{matrix} \Leftrightarrow \{\begin{matrix} x = 4 \\ \frac{(y - 3) (y - 2)}{(y + 1) (y + 2)} = \frac{1}{3} (*) \end{matrix} \\ (*) \Leftrightarrow 3 y^{2} - 15 y + 18 = y^{2} + 3 y + 2 \\ \Leftrightarrow 2 y^{2} - 18 y + 16 = 0 \Leftrightarrow [\begin{matrix} y = 8 (t m) \\ y = 1 (k t m) \end{matrix} \end{array}$

Vậy hệ phương trình có 1

nghiệm (x;y)=(4;8)

Đáp án cần chọn là: B

Câu 11:

Có bao nhiêu giá trị của n thỏa mãn bất đẳng thức: $C_{n - 1}^{4} - C_{n - 1}^{3} - \frac{5}{4} A_{n - 2}^{2} < 0$ (n∈N)?

A. 4

B. 5

C. 6

D. 8

Xem đáp án

ĐK: $\{\begin{matrix} n - 1 \geq 4 \\ n - 1 \geq 3 \\ n - 2 \geq 2 \end{matrix}$ ⇔n≥5,n∈N

$\begin{array}{l} C_{n - 1}^{4} - C_{n - 1}^{3} - \frac{5}{4} A_{n - 2}^{2} < 0 \\ \Leftrightarrow \frac{(n - 1)!}{4! (n - 5)!} - \frac{(n - 1)!}{3! (n - 4)!} - \frac{5}{4} \frac{(n - 2)!}{(n - 4)!} < 0 \\ \frac{(n - 2)!}{(n - 5)!} (\frac{n - 1}{4!} - \frac{n - 1}{3! (n - 4)} - \frac{5}{4 (n - 4)}) < 0 \\ \Leftrightarrow \frac{n - 1}{24} - \frac{n - 1}{6 (n - 4)} - \frac{5}{4 (n - 4)} < 0 \\ \Leftrightarrow \frac{(n - 1) (n - 4) - 4 (n - 1) - 30}{24 (n - 4)} < 0 \end{array}$

Vì n≥5⇒n−4>0 nên

bpt⇔ $\begin{array}{l} \{\begin{matrix} (n - 1) (n - 4) - 4 (n - 1) - 30 < 0 \\ n \geq 5 \end{matrix} \\ \Leftrightarrow \{\begin{matrix} n^{2} - 9 n - 22 < 0 \\ n \geq 5 \end{matrix} \Leftrightarrow \{\begin{matrix} - 2 \leq n < 11 \\ n \geq 5 \end{matrix} \end{array}$

$\Leftrightarrow 5 \leq n < 11$

Vì n∈N⇒n∈{5;6;7;8;9;10}

Vậy có 6 giá trị của n thỏa mãn

yêu cầu bài toán.

Đáp án cần chọn là: C

Câu 12:

Với x,y thỏa mãn hệ phương trình $\{\begin{matrix} A_{x}^{2} + C_{y}^{3} = 22 \\ A_{y}^{3} + C_{x}^{2} = 66 \end{matrix}$ (x,y∈N) thì x−y bằng?

A. -1

B. -2

C. 1

D. 2

Xem đáp án

ĐK: x≥2,y≥3,x,y∈N

Ta có: $C_{x}^{2} = \frac{1}{2} A_{x}^{2} = \frac{1}{2}; C_{y}^{3} = \frac{1}{3!} A_{y}^{3} = \frac{1}{6} A_{y}^{3}$

Đặt $A_{x}^{2} = a; A_{y}^{3} = b$ ta có:

hpt⇔ $\{\begin{matrix} a + \frac{b}{6} = 22 \\ b + \frac{a}{2} = 66 \end{matrix} \Leftrightarrow \{\begin{matrix} a = 12 \\ b = 60 \end{matrix} \Leftrightarrow \{\begin{matrix} A_{x}^{2} = 12 (1) \\ A_{y}^{3} = 60 (2) \end{matrix}$

Giải (1):

$\begin{array}{l} A_{x}^{2} = 12 \Leftrightarrow \frac{x!}{(x - 2)!} = 12 \Leftrightarrow x (x - 1) = 12 \\ \Leftrightarrow x^{2} - x - 12 = 0 \Leftrightarrow [\begin{matrix} x = 4 (t m) \\ x = - 3 (k t m) \end{matrix} \end{array}$

Giải (2):

$\begin{array}{l} A_{y}^{3} = 60 \Leftrightarrow \frac{y!}{(y - 3)!} = 60 \\ \Leftrightarrow y (y - 1) (y - 2) = 60 \\ \Leftrightarrow y^{3} - 3 y^{2} + 2 y - 60 = 0 \\ \Leftrightarrow y = 5 (t m) \end{array}$

Vậy x-y=4-5=-1

Đáp án cần chọn là: A

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Hoán vị chỉnh hợp tổ hợp có đáp án

Trắc nghiệm Hoán vị chỉnh hợp tổ hợp có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương