50 câu hỏi trắc nghiệm thuộc Đề ôn luyện thi thpt quốc gia môn Toán cực hay có lời giải chi tiết - đề 14

Câu 1:

Tính môđun của số phức $z = 1 + 4 i + {(1 - i)}^{3}$ .

A. 4

B. $\sqrt{29}$

C. 1

D. $\sqrt{5}$

Xem đáp án

Chọn D

Câu 2:

Tìm tập xác định của hàm số $y = \frac{2}{\log_{4} x - 3}$ .

A. (0;64)

B. $(0; 64) \cup (64; + \infty)$

C. $(- \infty; 0) \cup (64; + \infty)$

D. $(- 64; 0) \cup (64; + \infty)$

Xem đáp án

Chọn B

Câu 3:

Trong không gian, cho hình chữ nhật ABCD có AB = 2, AD = 3. Đường thẳng d nằm trong mặt phẳng (ABCD), không có điểm chung với ABCD, song song với cạnh AB và cách AB một khoảng bằng 1. Tính thể tích V của khối tròn xoay, nhận được khi quay hình chữ nhật ABCD quanh trục d.

A. $V = 17 π$

B. $V = 5 π$

C. $V = 15 π$

D. $V = 30 π$

Xem đáp án

Chọn D

Câu 4:

Tìm số phức z, biết $z^{2} - 5 (1 + i) z - 6 - 5 i = 0$ .

A. $z_{1} = 1; z_{2} = - 6 - 5 i$

B. $z_{1} = - 1; z_{2} = 6 + 5 i$

C. $z_{1} = - 1; z_{2} = - 6 - 5 i$

D. $z_{1} = 1; z_{2} = 6 + 5 i$

Xem đáp án

Chọn B

Câu 5:

Hàm số $y = \frac{2 x - 1}{x + 1}$ có bảng biến thiên là bảng nào trong các bảng dưới đây?

A.

B.

C.

D.

Xem đáp án

Chọn D

Câu 6:

Cho hình chóp S.ABCD. Gọi M, N, P lần lượt là trung điểm của các cạnh SA, SB,SC. Mặt phẳng (MNP) cắt cạnh SD tại điểm Q. Đặt $t = \frac{V_{S . M N P Q}}{V_{S . A B C D}}$ . Tìm t.

A. $t = \frac{1}{16}$

B. $t = \frac{1}{8}$

C. $t = \frac{1}{2}$

D. $t = \frac{1}{4}$

Xem đáp án

Chọn B

Câu 7:

Cho hàm số $y = \frac{x + 1}{x - 2}$ . Khẳng định nào sau đây là đúng?

A. Hàm số đồng biến trên khoảng $(- 1; + \infty)$

B. Hàm số nghịch biến trên R.

C. Hàm số đồng biến trên $(2; + \infty)$

D. Hàm số nghịch biến trên khoảng $(- \infty; 2)$

Xem đáp án

Chọn D

Câu 8:

Tìm nguyên hàm của hàm số $f (x) = {(x - 1)}^{2}$ .

A. $\int f (x) d x = \frac{{(x - 1)}^{2}}{2} + C$

B. $\int f (x) d x = 2 (x - 1) + C$

C. $\int f (x) d x = \frac{{(x - 1)}^{3}}{3} + C$

D. $\int f (x) d x = \frac{x^{3}}{3} + C$

Xem đáp án

Chọn C

Câu 9:

Tìm số nghiệm của phương trình $3^{1 - 2 x} . 27^{\frac{x + 1}{3}} = 81$

A. 2

B. 1

C. 3

D. 0

Xem đáp án

Chọn B

Câu 10:

Cho $F (x) = - \frac{1}{3 x^{3}}$ là một nguyên hàm của hàm số $\frac{f (x)}{x}$ . Tìm nguyên hàm của hàm số $f' (x) \ln x$

A. $\int f' (x) d x = \frac{\ln x}{x^{3}} + \frac{1}{3 x^{3}} + C$

B. $\int f' (x) d x = - \frac{\ln x}{x^{3}} + \frac{1}{3 x^{3}} + C$

C. $\int f' (x) d x = - \frac{\ln x}{x^{3}} + \frac{1}{5 x^{3}} + C$

D. $\int f' (x) d x = \frac{\ln x}{x^{3}} + \frac{1}{5 x^{3}} + C$

Xem đáp án

Chọn A

Câu 11:

Tìm tọa độ tâm đối xứng của đồ thị hàm số $y = x^{3} - 3 x + 1$

A. (-1;4)

B. (0;2)

C. (1;0)

D. đồ thị không có tâm đối xứng

Xem đáp án

Chọn B

Câu 12:

Cho a là số dương, đơn giản biểu thức $\frac{a^{\frac{4}{3}} (a^{- \frac{1}{3}} + a^{\frac{2}{3}})}{a^{\frac{1}{4}} (a^{\frac{3}{4}} + a^{- \frac{1}{4}})}$ .

A. a

B. 2a

C. $\frac{1}{a}$

D. $\frac{2}{a}$

Xem đáp án

Chọn A

Câu 13:

Cho điểm A(-4;1;3) và đường thẳng $d : \frac{x + 1}{- 2} = \frac{y - 1}{1} = \frac{z + 3}{3}$ . Viết phương trình mặt phẳng (P) qua A và vuông góc với đường thẳng d

A. $2 x - y - 3 z + 36 = 0$

B. $2 x - y - 3 z - 18 = 0$

C. $2 x - y + 3 z = 0$

D. $2 x - y - 3 z + 18 = 0$

Xem đáp án

Chọn D

Câu 14:

Biết $a < b < c, \int_{a}^{c} f (x) d x = 15$ và $\int_{b}^{c} f (x) d x = 8$ . Tính giá trị của $I = \int_{a}^{b} f (x) d x$ .

A. I = -7

B. I = 120

C. I = 7

D. I = 23

Xem đáp án

Chọn C

Câu 15:

Hỏi $z = 1 - 2 i$ và $z = 3 i$ là các nghiệm của phương trình nào trong các phương trình sau?

A. $5 x^{3} - 3 x + 3 = 0$

B. $- 2 x^{2} - 3 x + 5 = 0$

C. $x^{2} - (1 + i) x + 6 + 3 i = 0$

D. $\frac{4}{9} x^{2} + 5 x + 4 - 15 i = 0$

Xem đáp án

Chọn C

Câu 16:

Cho hàm số $y = \frac{x + 1}{\sqrt{x^{2} + 1}}$ . Khẳng định nào sau đây là sai?

A. Hàm số đạt cực tiểu tại điểm x = 1

B. Hàm số đạt cực đại tại điểm x = 1

C. Hàm số có một cực trị là $y = \sqrt{2}$

D. Tập xác định của hàm số là R

Xem đáp án

Chọn A

Câu 17:

Cho mặt phẳng $(P) : 2 x + 3 y + z - 11 = 0$ . Viết phương trình mặt cầu (S) có tâm I(1;-2;1) và tiếp xúc với (P).

A. ${(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 1)}^{2} = 12$

B. ${(x + 1)}^{2} + {(y - 2)}^{2} + {(z + 1)}^{2} = 12$

C. ${(x - 1)}^{2} + {(y + 2)}^{2} + {(z - 1)}^{2} = 14$

D. ${(x - 1)}^{2} + {(y + 2)}^{2} + {(z - 1)}^{2} = 16$

Xem đáp án

Chọn C

Câu 18:

Cho hình chóp S.ABC, G là trọng tâm ABC. Khi quay các cạnh của hình chóp S.ABC xung quanh trục SG, hỏi có tất cả bao nhiêu hình nón được tạo thành?

A. Ba hình nón

B. Hai hình nón

C. Một hình nón

D. Không có hình nón nào

Xem đáp án

Chọn C

Câu 19:

Hàm số $y = - x^{3} - x + 5$ có tất cả bao nhiêu điểm cực trị?

A. có 1 điểm cực trị

B. không có cực trị

C. có 2 điểm cực trị

D. có vô số điểm cực trị

Xem đáp án

Chọn B

Câu 20:

Viết phương trình mặt phẳng (Q) chứa trục tung và đi qua A(1;4;-3).

A. $3 x + z = 0$

B. $3 x + z + 1 = 0$

C. $4 x - y = 0$

D. $3 x - z = 0$

Xem đáp án

Chọn A

Câu 21:

Trong một buổi liên hoan có 10 cặp nam nữ, trong đó có 4 cặp vợ chồng. Chọn ngẫu nhiên 3 người để biểu diễn một tiết mục văn nghệ. Xác suất để 3 người được chọn không có một cặp vợ chồng nào là

A. $\frac{8}{95}$

B. $\frac{43}{65}$

C. $\frac{27}{65}$

D. $\frac{89}{65}$

Xem đáp án

Chọn D

Câu 22:

Cho hàm số $y = x^{3} - 3 x^{2} + 4 (C)$ . Tiếp tuyến của đồ thị (C) song song với đường thẳng y = -3x có phương trình là:

A. $y = - 3 x + 2$

B. $y = - 3 x + 3$

C. $y = - 3 x + 4$

D. $y = - 3 x + 5$

Xem đáp án

Chọn D

Câu 23:

Cho hai đường thẳng $d_{1} : \frac{x - 8}{1} = \frac{y - 5}{2} = \frac{z - 8}{- 1}$ và $d_{2} : \frac{x - 3}{7} = \frac{y - 1}{2} = \frac{z - 1}{3}$ . Viết phương trình mặt phẳng (P) chứa $d_{1}$ và (P) song song với $d_{2}$ .

A. $4 x + 5 y + 6 z - 41 = 0$

B. $4 x - 5 y - 6 z + 41 = 0$

C. $4 x + 5 y - 6 z + 41 = 0$

D. $4 x + 5 y + 6 z + 41 = 0$

Xem đáp án

Chọn B

Câu 24:

Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số $y = 2 \sin^{2} x + \cos^{2} 2 x$

A. $m a x y = \frac{3}{2}, m i n y = \frac{1}{2}$

B. $m a x y = 3, m i n y = - \frac{1}{2}$

C. $m a x y = \frac{1}{2}, m i n y = - \frac{1}{2}$

D. $m a x y = 3, m i n y = \frac{3}{4}$

Xem đáp án

Chọn D

Câu 25:

Cho hàm số $f (x) = a x + 1 + \sqrt{b^{2} x^{2} + 1}$ . Giới hạn $\lim_{x \to \pm \infty} f (x)$ là hữu hạn khi

A. $a = \pm b$

B. $a = \pm 2 b$

C. $a = \pm \frac{1}{2} b$

D. $a + b = 1$

Xem đáp án

Chọn A

Câu 26:

Viết phương trình mặt phẳng (P) song song và cách đều hai đường thẳng: $d_{1} : \frac{x - 2}{1} = \frac{y}{1} = \frac{z}{1}; d_{2} : \frac{x}{2} = \frac{y - 1}{- 1} = \frac{z - 2}{- 1}$ .

A. $(P) : 2 x - 2 z + 1 = 0$

B. $(P) : 2 x - 2 z - 1 = 0$

C. $(P) : 2 y - 2 z + 1 = 0$

D. $(P) : 2 y - 2 z - 1 = 0$

Xem đáp án

Chọn A

Câu 27:

Cho hình lập phương $A B C D . A^{'} B' C' D'$ . Xét (P) là mặt phẳng thay đổi luôn chứa đường thẳng $C D'$ . Giá trị nhỏ nhất của số đo góc giữa mặt phẳng (P) và mặt phẳng ( $B D D' B'$ ) bằng

A. $60^{0}$

B. $30^{0}$

C. $45^{0}$

D. $0^{0}$

Xem đáp án

Chọn A

Câu 28:

Cho tứ diện ABCD có $A B = C D = a, A C = B D = b, A D = B C = c$ . Gọi $α$ là số đo của góc hợp bởi hai đường thẳng AB, CD. Khi đó $\cos α$ bằng

A. $\frac{|b^{2} - c^{2}|}{a^{2}}$

B. $\frac{|b^{2} - c^{2}|}{2 a^{2}}$

C. $\frac{a^{2}}{2 (b^{2} + c^{2})}$

D. $\frac{a^{2}}{b^{2} + c^{2}}$

Xem đáp án

Chọn A

Câu 29:

Cho $I = \int_{1}^{2} 2 x \sqrt{x^{2} - 1} d x$ và $u = x^{2} - 1$ . Chọn khẳng định sai trong các khẳng định sau:

A. $I = \frac{2}{3} \sqrt{27}$

B. $I = \int_{1}^{2} \sqrt{u} d u$

C. $I = \frac{2}{3} u^{\frac{2}{3}}_{0}^{3}$

D. $I = \int_{0}^{3} \sqrt{u} d u$

Xem đáp án

Chọn B

Câu 30:

Xét dãy số $(u_{n}), n \in N *$ được xác định bởi $\{\begin{cases} u_{1} = 3 \\ u_{n + 1} = \frac{1}{2} u_{n} \end{cases}$ .Tìm $u_{10}$

A. $u_{10} = \frac{3}{512}$

B. $u_{10} = \frac{3}{1024}$

C. $u_{10} = \frac{1}{1024}$

D. $u_{10} = \frac{1}{512}$

Xem đáp án

Chọn A

Câu 31:

Tìm nguyên hàm của hàm số $f (x) = \frac{e^{\sqrt{x}}}{\sqrt{x}}$

A. $\int f (x) d x = 2 e^{\sqrt{x}} + C$

B. $\int f (x) d x = e^{2 \sqrt{x}} + C$

C. $\int f (x) d x = \frac{e^{\sqrt{x}}}{2} + C$

D. $\int f (x) d x = e^{\sqrt{x}} + C$

Xem đáp án

Chọn A

Câu 32:

Tính thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường thẳng $y = \cos x, y = 0, x = 0, x = π$ quay quanh trục Ox.

A. $\frac{π}{3}$

B. $\frac{π^{2}}{2}$

C. $\frac{π}{2}$

D. $\frac{π^{2}}{3}$

Xem đáp án

Chọn B

Câu 33:

Cho hình lăng trụ tam giác đều ABC.A’B’C’ có mặt phẳng (ABC’) tạo với đáy góc $60^{0}$ diện tích tam giác ABC’ bằng $24 \sqrt{3} c m^{2}$ . Tính thể tích V của khối lăng trụ ABC.A’B’C’.

A. $V = 724 c m^{2}$

B. $V = 345 c m^{2}$

C. $V = 216 c m^{2}$

D. $V = 820 c m^{2}$

Xem đáp án

Chọn C

Câu 34:

Cho mặt phẳng $(P) : x - 2 y + z - 4 = 0$ và đường thẳng $d : \frac{x - 3}{3} = \frac{y + 5}{- 5} = \frac{z - 3}{- 1}$ . Viết phương trình hình chiếu vuông góc của d trên (P).

A. $\{\begin{cases} x = t \\ y = - t \\ z = 4 - 3 t \end{cases}$

B. $\{\begin{cases} x = - t \\ y = t \\ z = 4 - 3 t \end{cases}$

C. $\{\begin{cases} x = - t \\ y = t \\ z = 4 - 4 t \end{cases}$

D. $\{\begin{cases} x = - t \\ y = t \\ z = 4 + 4 t \end{cases}$

Xem đáp án

Chọn A

Tìm giao điểm I của d và (P). Hình chiếu vuông góc của đường thẳng qua điểm I và nhận vecto chỉ phương là tích có hướng của hai vecto: vecto pháp tuyến của mặt phẳng (P) và vecto pháp tuyến của mặt phẳng chứa d vuông góc với (P).

Câu 35:

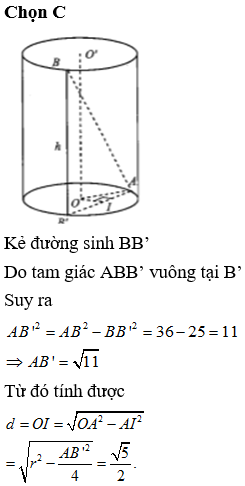
Cho hình nón tròn xoay có đường cao $h = \sqrt{5}$ , bán kính đáy r = 3. Mặt phẳng (P) qua đỉnh của hình nón nhưng không qua trục của hình nón và cắt hình nón theo giao tuyến là một tam giác cân có độ dài cạnh đáy bằng 4. Gọi O là tâm của hình tròn đáy. Tính khoảng cách d từ điểm O đến mặt phẳng (P).

A. $d = \frac{\sqrt{5}}{2}$

B. $d = \sqrt{10}$

C. $d = \sqrt{5}$

D. $d = \frac{\sqrt{10}}{2}$

Xem đáp án

Chọn D

Câu 36:

tập hợp tất cả các giá trị của tham số m để qua điểm M(2;m) kẻ được ba tiếp tuyến đến đồ thị hàm số $y = x^{3} - 3 x^{2}$ là

A.(-5;-4)

B. (-2;3)

C. (-5;4)

D. (4;5)

Xem đáp án

Chọn A

Câu 37:

Trong mặt phẳng tọa độ Oxy, tìm tập hợp các điểm M biểu diễn số phức z có phần thực dương, thỏa mãn $|z| \leq 2$

A. Đường tròn (O;2)

B. Hình tròn (O;2)

C. Nửa hình tròn (O;2) nằm bên trái trục tung

D. Nửa hình tròn (O;2) nằm bên phải trục tung

Xem đáp án

Chọn D

Câu 38:

Hình bên là đồ thị của hàm số $y = 2 x^{4} - 4 x^{2} + 1$ . Tìm tất cả các giá trị thực của tham số m để phương trình $|2 x^{4} - 4 x^{2} + 1| = 1 - m$ có 4 nghiệm phân biệt.

A. m = 0

B. m < 0

C. 0 < m < 1

D. m = 1

Xem đáp án

Chọn D

Câu 39:

Tìm hệ số chứa $x^{10}$ trong khai triển $f (x) = {(\frac{1}{4} x^{2} + x + 1)}^{2} {(x + 2)}^{3 n^{}}$ với n là số tự nhiên thỏa mãn hệ thức $A_{n}^{3} + C_{n}^{n - 2} = 14 n$

A. $2^{5} C_{19}^{10}$

B. $2^{5} C_{19}^{10} x^{10}$

C. $2^{9} C_{19}^{10}$

D. $2^{9} C_{19}^{10} x^{10}$

Xem đáp án

Chọn A

Câu 40:

Biết $4^{x} + 4^{- x} = 23$ . Tính $I = 2^{2} + 2^{- x}$ .

A. I = 5

B. I = 4

C. $I = \sqrt{23}$

D. $I = \sqrt{21}$

Xem đáp án

Chọn A

Câu 41:

Cho hình lăng trụ $A B C . A' B' C'$ có $A B = 1, A C = \sqrt{2}, ∠ C A B = 135^{0}, A A' = 1$ . Hình chiếu vuông góc của điểm A trên mặt phẳng (A’B’C’) trùng với trung điểm H của B’C’, Số đo của góc hợp bởi đường thẳng AH và mặt phẳng (ABB’A’) bằng

A. $30^{0}$

B. $60^{0}$

C. $45^{0}$

D. $90^{0}$

Xem đáp án

Chọn A

Câu 42:

Tìm nghiệm của phương trình $\frac{4}{4 + \log_{a} x} + \frac{2}{2 - \log_{a} x} = 1$ , với a > 1.

A. $[\begin{matrix} x = \frac{1}{a^{2}} \\ x = \frac{1}{a^{4}} \end{matrix}$

B. $[\begin{matrix} x = \frac{1}{a} \\ x = \frac{1}{a^{4}} \end{matrix}$

C. $[\begin{matrix} x = \frac{1}{a} \\ x = \frac{1}{a^{2}} \end{matrix}$

D. $[\begin{matrix} x = 1 \\ x = \frac{1}{a^{2}} \end{matrix}$

Xem đáp án

Chọn C

Câu 43:

Tìm giá trị lớn nhất của hàm số $y = \sin^{4} x + \cos^{4} x - \sin x . \cos x$ .

A. $m a x y = \frac{1}{2}$

B. $m a x y = \frac{9}{8}$

C. $m a x y = \frac{1}{4}$

D. $m a x y = \frac{3}{4}$

Xem đáp án

Câu 44:

Nghiệm của phương trình $4 . 2^{x} = {(\sqrt{2})}^{4 - 2 x} + 15$ là

A. 9

B. 27

C. 2

D. 6

Xem đáp án

Chọn C

Câu 45:

Cho ba điểm A(1;1;1), B(-1;-1;0), C(3;1;-1). Tìm tọa độ điểm N trên mặt phẳng (Oxy) cách đều ba điểm A, B, C.

A. $N (2; - \frac{4}{7}; 0)$

B. N(2;0;0)

C. $N (2; \frac{7}{4}; 0)$

D. N(0;0;2)

Xem đáp án

Chọn A
Điểm N(x;y;0). Tìm x;y từ hệ hai phương trình NA = NB = NC.

Câu 46:

Cho mặt phẳng $(P) : x - 2 y + 2 z + 1 = 0$ cắt mặt cầu (S) có phương trình $(S) : x^{2} + y^{2} + z^{2} - 4 x + 6 y + 6 z + 17 = 0$ theo đường tròn. Tính chu vi của đường tròn đó.

A. $4 π$

B. $π$

C. $6 π$

D. $8 π$

Xem đáp án

Chọn A

Tìm tọa độ tâm I và bán kính R của mặt cầu, tính khoảng cách d từ tâm I đến mặt phẳng (P). Bán kính của đường tròn $r = \sqrt{R^{2} - d^{2}}$ . Công thức tính chu vi đường tròn là $C = 2 π r$ .

Câu 47:

Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số $y = x^{3} - 3 m x^{2} + 4 m^{3}$ có hai điểm cực trị A và B sao cho $A B = \sqrt{20}$

A. $m \in \{- 1; 2\}$

B. không có giá trị của m.

C. $m \in \{- 1; 1\}$

D. $m \in \{- 2; 1\}$

Xem đáp án

Câu 48:

Trong hội nghị học sinh giỏi của trường, khi ra về các em bắt tay nhau. Có 120 cái bắt tay và giả sử không em nào bỏ sót cũng như bắt tay lặp lại 2 lần. Số học sinh dự hội nghị thuộc khoảng nào sau đây?

A.(13;18)

B. (9;14)

C. (17;22)

D. (21;26)

Xem đáp án

Chọn A

Câu 49:

Cho hình trụ có chiều cao h = 5, bán kính đáy r = 2. Một đoạn thẳng có chiều dài bằng 6 và có hai đầu mút nằm trên hai đường tròn đáy. Tính khoảng cách d từ đoạn thẳng đó đến trục của hình trụ.

A. $d = \frac{\sqrt{11}}{2}$

B. d = 2

C. $d = \frac{\sqrt{5}}{2}$

D. $d = 4 \sqrt{2}$

Xem đáp án

Câu 50:

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, $∠ B A D = 60^{0}$ , cạnh bên SA vuông góc với đáy. Biết rằng góc giữa hai mặt phẳng (SBC) và (SCD) bằng $60^{0}$ Độ dài đoạn thẳng SA bằng

A. $\frac{a \sqrt{6}}{4}$

B. $\frac{a \sqrt{6}}{2}$

C. $\frac{a \sqrt{3}}{2}$

D. $\frac{a \sqrt{3}}{4}$

Xem đáp án

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề ôn luyện thi thpt quốc gia môn Toán cực hay có lời giải chi tiết

Đề ôn luyện thi thpt quốc gia môn Toán cực hay có lời giải chi tiết - đề 14

Danh sách câu hỏi

Bài thi liên quan