Giải SBT Toán 11 Chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng
Giải SBT Bài 5: Phép quay
-
2763 lượt thi
-
4 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
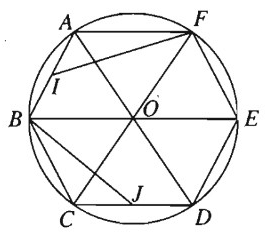
Cho lục giác đều ABCDEF, O là tâm đối xứng của nó, I là trung điểm của AB
a) Tìm ảnh của tam giác AIF qua phép quay tâm O góc
b) Tìm ảnh của tam giác AOF qua phép quay tâm E góc
Xem đáp án
a) Phép quay tâm O góc biến F, A, B lần lượt thành B, C, D; biến trung điểm I của AB thành trung điểm J của CD. Nên nó biến tam giác AIF thành tam giác CJB.
b) Phép quay tâm E góc biến A, O, F lần lượt thành C, D, O.
Câu 2:
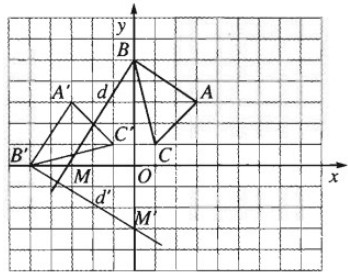
Trong mặt phẳng Oxy cho các điểm A(3; 3), B(0; 5), C(1; 1) và đường thẳng d có phương trình . Hãy xác định tọa độ các đỉnh của tam giác A’B’C’ và phương trình của đường thẳng d theo thứ tự là ảnh của tam giác ABC và đường thẳng d qua phép quay tâm O, góc quay
Xem đáp án
Gọi Q(0;) là phép quay tâm O, góc quay .
A′(−3;3)
B′(5;0)
C′(−1;1)
d đi qua B và M(−3; 0)
M′ = Q(0;); M=(0; −3) nên d' là đường thẳng B'M' có phương trình 3x + 5y + 15 = 0
Câu 3:
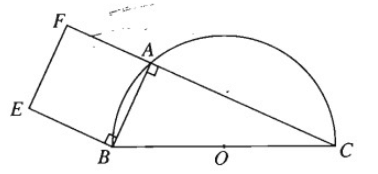
Cho nửa đường tròn tâm O đường kính BC. Điểm A chạy trên nửa đường tròn đó. Dựng về phía ngoài của tam giác ABC hình vuông ABEF. Chứng minh rằng E chạy trên một nửa đường tròn cố định.
Xem đáp án
Xem E là ảnh của A qua phép quay tâm B, góc . Khi A chạy trên nửa đường tròn (O), E sẽ chạy trên nửa đường tròn (O') là ảnh của nửa đường tròn (O) qua phép quay tâm tâm B, góc .
Câu 4:
Cho tam giác ABC. Dựng về phía ngoài của tam giác các hình vuông BCIJ, ACMN, ABEF và gọi O, P, Q lần lượt là tâm đối xứng của chúng
a) Gọi D là trung điểm của AB. Chứng minh rằng DOP là tam giác vuông cân đỉnh D
b) Chứng minh AO vuông góc với PQ và AO = PQ
Xem đáp án
a) Phép quay tâm C góc biến MB thành AI. Do đó MB bằng và vuông góc với AI. DP song song và bằng nửa BM, DO song song và bằng nửa AI. Từ đó suy ra DP bằng và vuông góc với DO.
b) Từ câu a) suy ra phép quay tâm D, góc biến O thành P, biến A thành Q. Do đó OA bằng và vuông góc với PQ.