Giải SBT Toán 11 Chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng
Giải SBT Bài 4: Phép đối xứng tâm
-
2767 lượt thi
-
4 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
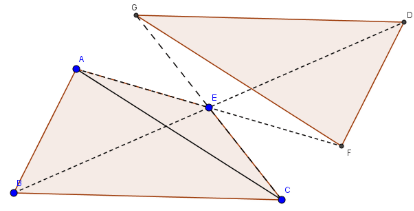
Cho tứ giác ABCE. Dựng ảnh của tam giác ABC qua phép đối xứng tâm E.
Xem đáp án
Dựng ảnh của từng điểm qua phép đối xứng tâm E ta được hình sau:
Câu 2:
Trong mặt phẳng Oxy, cho hai điểm I(1; 2), M(-2; 3), đường thẳng d có phương trình và đường tròn (C) có phương trình: .
Hãy xác định tọa độ của điểm M’, phương trình của đường thẳng d’ và đường tròn (C’) theo thứ tự là ảnh của M, d và (C) qua
a) Phép đối xứng qua gốc tọa độ;
b) Phép đối xứng qua tâm I.
Xem đáp án
a) Gọi M', d' và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua O. Dùng biểu thức tọa độ của phép đối xứng qua gốc tọa độ ta có :
M′ = (2; −3), phương trình của d′: 3x – y – 9 = 0, phương trình của đường tròn (C′): .
b) Gọi M', d' và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua I .
Vì I là trung điểm của MM' nên M′ = (4;1)
Vì d' song song với d nên d' có phương trình 3x – y + C = 0. Lấy một điểm trên d, chẳng hạn N(0; 9). Khi đó ảnh của N qua phép đối xứng qua tâm I là N′(2; −5). Vì N' thuộc d nên ta có 3.2 − (−5) + C = 0. Từ đó suy ra C = -11.
Vậy phương trình của d' là 3x – y – 11 = 0.
Để tìm (C'), trước hết ta để ý rằng (C) là đường tròn tâm J(−1; 3), bán kính bằng 2. Ảnh của J qua phép đối xứng qua tâm I là J′(3; 1). Do đó (C') là đường tròn tâm J' bán kính bằng 2. Phương trình của (C') là .
Câu 3:
Trong mặt phẳng Oxy, cho đường thẳng d có phương trình: và d đường thẳng có phương trình:
. Tìm phép đối xứng tâm biến d thành d’ và biến trục Ox thành chính nó.
Xem đáp án
Giao của d và d' với lần lượt là A(−2; 0) và A′(8;0). Phép đối xứng qua tâm cần tìm biến A thành A' nên tâm đối xứng của nó là I = (3;0).
Câu 4:
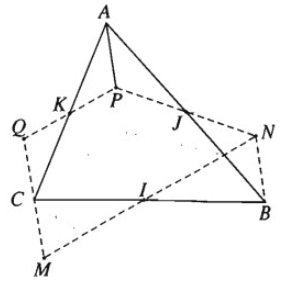
Cho ba điểm I, J, K không thẳng hàng. Hãy dựng tam giác ABC nhận I, J, K lần lượt là trung điểm của các cạnh BC, AB, AC
Xem đáp án
Giả sử tam giác ABC đã dựng được. Lấy điểm M bất kì. Gọi N là ảnh của M qua phép đối xứng tâm I. P là ảnh của N qua phép đối xứng tâm J. Q là ảnh của P qua phép đối xứng tâm K. Khi đó . Do đó C là trung điểm của QM. Từ đó suy ra cách dựng tam giác ABC.