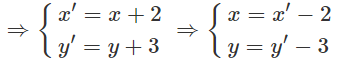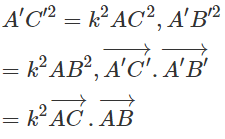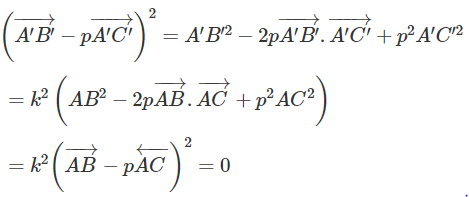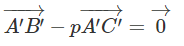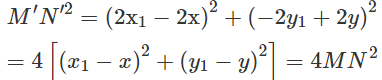12 câu hỏi trắc nghiệm thuộc GiảI SBT Câu hỏi ôn tập chương 1

Câu 1:

Trong mặt phẳng Oxy cho đường thẳng d có phương trình $3 x - 5 y + 3 = 0$ và vectơ $\vec{v}$ = (2;3). Hãy viết phương trình đường thẳng d’ là ảnh của d qua phép tịnh tiến theo vectơ $\vec{v}$ .

Xem đáp án

Gọi M′(x′;y′) ∈ d′ là ảnh của M(x,y) ∈ d qua phép tịnh tiến theo vecto $\vec{v}$ (2;3)

Do M(x,y) ∈ d nên

3x − 5y + 3 = 0

⇒ 3(x′−2) − 5(y′−3) + 3 = 0

⇔ 3x′ − 5y′ + 12 = 0 (d′)

Vậy M′(x′;y′) ∈ d′: 3x′ − 5y′ + 12 = 0

Câu 2:

Cho hình bình hành ABCD có ABcố định, đường chéo ACcó độ dài bằng m không đổi. Chứng minh rằng khi C thay đổi, tập hợp các điểm D thuộc một đường tròn cố định.

Xem đáp án

Xem D là ảnh của C qua phép tịnh tiến theo vectơ $\vec{BA}$ . Do C chạy trên đường tròn (C) tâm A bán kính m, trừ ra giao điểm của (C) với đường thẳng AB, nên D thuộc đường tròn là ảnh của đường tròn nói trên qua phép tịnh tiến theo vectơ $\vec{BA}$ .

Câu 3:

Cho tam giác ABC. Tìm một điểm M trên cạnh AB và một điểm N trên cạnh AC sao cho MN song song với BC và AM = CN.

Xem đáp án

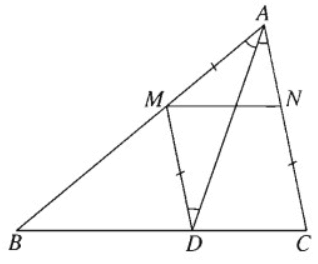
Giả sử đã dựng được hai điểm M, N thỏa mãn điều kiện đầu bài. Đường thẳng qua M và song song với AC cắt BC tại D. Khi đó tứ giác MNCD là hình bình hành. Do đó CN = DM. Từ đó suy ra tam giác AMD cân tại M. Do đó 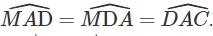. Suy ra AD là phân giác trong của góc A. Do đó AD dựng được .Ta lại có $\vec{NM} = \vec{CD}$ , nên có thể xem M là ảnh của N qua phép tịnh tiến theo vectơ $\vec{DC}$ .

Từ đó suy ra cách dựng:

- Dựng đường phân giác trong của góc A. Đường này cắt BC tại D.

- Dựng đường thẳng d là ảnh của đường thẳng AC qua phép tịnh tiến theo vectơ $\vec{CD}$ . d cắt AB tại M.

- Dựng N sao cho $\vec{NM} = \vec{CD}$ .

Khi đó dễ thấy M, N thỏa mãn điều kiện đầu bài.

Câu 4:

Trong mặt phẳng Oxy cho đường thẳng d có phương trình $3 x - 2 y - 6 = 0$

a) Viết phương trình của đường thẳng $d_{1}$ là ảnh của d qua phép đối xứng qua trục Oy

b) Viết phương trình của đường thẳng $d_{2}$ là ảnh của d qua phép đối xứng qua đường thẳng Δ có phương trình

$x + y - 2 = 0$ .

Xem đáp án

a) $d_{1}$ : 3x + 2y + 6 = 0

b) Giao của d và Δ là A(2;0). Lấy B(0; −3) thuộc d. Ảnh của B qua phép đối xứng của đường thẳng Δ là B′(5;2). Khi đó d' chính là đường thẳng AB′: 2x − 3y – 4 = 0

Câu 5:

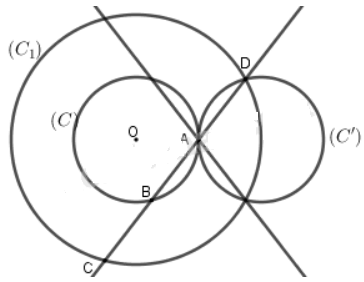
Cho đường tròn (C) và hai điểm cố định phân biệt A, B thuộc (C). Với mỗi điểm M chạy trên đường tròn (trừ hai điểm A, B), ta xét điểm N sao cho ABMN là hình bình hành. Chứng minh rằng tập hợp các điểm N cũng nằm trên một đường tròn xác định.

Xem đáp án

Tập hợp các điểm N thuộc đường tròn (C') là ảnh của (C) qua phép đối xứng qua trung điểm của AB.

Câu 6:

Cho hai đường tròn có cùng tâm O, bán kính lần lượt là R và r,(R > r). A là một điểm thuộc đường tròn bán kính r. Hãy dựng đường thẳng qua A cắt đường tròn bán kính r tại B, cắt đường tròn bán kính R tại C, D sao cho CD = 3AB.

Xem đáp án

Câu 7:

Trong mặt phẳng Oxy cho đường thẳng d có phương trình $x + y - 2 = 0$ . Hãy viết phương trình của đường thẳng d’ là ảnh của d qua phép quay tâm O góc $45 °$ .

Xem đáp án

Dễ thấy d chứa điểm H(1;1) và OH ⊥ d. Gọi H' là ảnh của H qua phép quay tâm O góc 45° thì H′ = ( $0; \sqrt{2}$ ). Từ đó suy ra d' phải qua H' và vuông góc với OH'. Vậy phương trình của d' là $y = \sqrt{2}$ .

Câu 8:

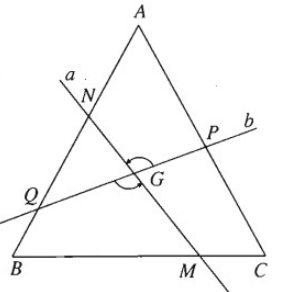
Qua tâm G của tam giác đều ABC, kẻ đường thẳng a cắt BC tại M và cắt AB tại N, kẻ đường thẳng b cắt AC tại P và AB tại Q, đồng thời góc giữa a và b bằng $60 °$ . Chứng minh rằng tứ giác MNPQ là một hình thang cân.

Xem đáp án

Gọi Q(G; $120 °$ ) là phép quay tâm G góc $120 °$ . Phép quay này biến b thành a, biến CA thành AB; do đó nó biến P thành N.

Tương tự Q(G; $120 °$ ) cũng biến Q thành M. Từ đó suy ra GP = GN, GQ = GM. Do đó hai tam giác GNQ và GPM bằng nhau, suy ra NQ = PM. Vì Q(G; $120 °$ ) biến PQ thành NM nên PQ = NM. Từ đó suy ra hai tam giác NQM và PMQ bằng nhau. Do đó $\hat{NQM} = \hat{PMQ}$ . Tương tự $\hat{QNP} = \hat{MPN}$ .

Từ đó suy ra $\hat{PNQ} + \hat{NQM} = 180 °$

Do đó NP // QM. Vậy ta có tứ giác MPNQ là hình thang cân.

Câu 9:

Gọi A', B', C' tương ứng là ảnh của ba điểm A, B, C qua phép đồng dạng tỉ số k. Chứng minh rằng:

$\vec{A' B'} . \vec{A' C'} = k^{2} \vec{AB} . \vec{AC}$ .

Xem đáp án

Theo định nghĩa của phép đồng dạng ta có $B ’ C ’ = kBC$ , từ đó suy ra $B' C'^{2} = k^{2} {BC}^{2}$ .

Hay ${(\vec{A' C'} - \vec{A' B'})}^{2} = k^{2} {(\vec{AC} - \vec{AB})}^{2}$ . Suy ra

$A' C'^{2} - 2 \vec{A' C'} . \vec{A' B'} + A' B'^{2} = k^{2} ({AC}^{2} - 2 \vec{AC} . \vec{AB} + {AB}^{2})$ .

Để ý rằng $A' C'^{2} = k^{2} {AC}^{2}, A' B'^{2} = k^{2} {AB}^{2}$ ta suy ra điều phải chứng minh.

Câu 10:

Gọi A’, B’ và C’ tương ứng là ảnh của ba điểm A, B và C qua phép đồng dạng. Chứng minh rằng nếu

$\vec{AB} = p \vec{AC}$ thì $\vec{A' B'} = p \vec{A' C'}$ , trong đó p là một số. Từ đó chứng minh rằng phép đồng dạng biến ba điểm thẳng hàng thành ba điểm thẳng hàng và nếu điểm B nằm giữa hai điểm A và C thì điểm B' nằm giữa hai điểm A’ và C’.

Xem đáp án

Để ý rằng

Ta có:

Từ đó suy ra

Giả sử ba điểm A, B, C thẳng hàng và điểm B nằm giữa hai điểm A và C. Khi đó $\vec{AB} = t \vec{AC}$ , với 0 < t < 1. Áp dụng bài 1.39 ta cũng có $\vec{A' B'} = t \vec{A' C'}$ , với 0 < t < 1. Do đó ba điểm A′, B′, C′ thẳng hàng và điểm B' nằm giữa hai điểm A' và C'.

Câu 11:

Trong mặt phẳng Oxy xét phép biến hình F biến mỗi điểm M(x;y) thành M′(2x − 1; −2y + 3). Chứng minh F là một phép đồng dạng.

Xem đáp án

Lấy điểm N(x1; y1), thì điểm N′(2x1 − 1; −2y1 + 3) = F(N). Ta có

Từ đó suy ra với hai điểm M, N tùy ý và M', N' lần lượt là ảnh của chúng qua F ta có M′N′ = 2MN. Vậy F là phép đồng dạng với tỉ số đồng dạng là 2.

Câu 12:

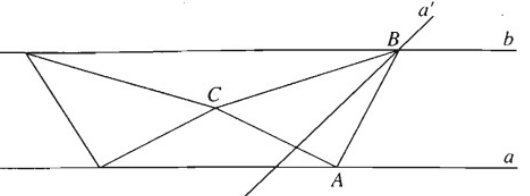
Dựng tam giác BAC vuông cân tại A có C là một điểm cho trước, còn hai đỉnh A, B lần lượt thuộc hai đường thẳng a, b song song với nhau cho trước.

Xem đáp án

Xem B là ảnh của A qua phép đồng dạng có được bằng cách thực hiện liên tiếp phéo quay tâm C góc $45 °$ hoặc $- 45 °$ và phép vị tự tâm C tỉ số $k = \sqrt{2}$ . Vì A thuộc a nên B thuộc đường thẳng a’ là ảnh của a qua phép đồng dạng nói trên. Vậy b là giao của a’ và b. Từ đó suy ra cách dựng . Bài toán có hai nghiệm hình.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải SBT Toán 11 Chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng

GiảI SBT Câu hỏi ôn tập chương 1

Danh sách câu hỏi

Bài thi liên quan