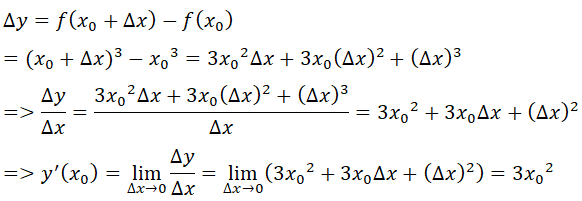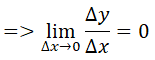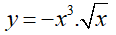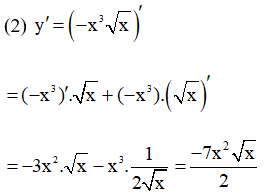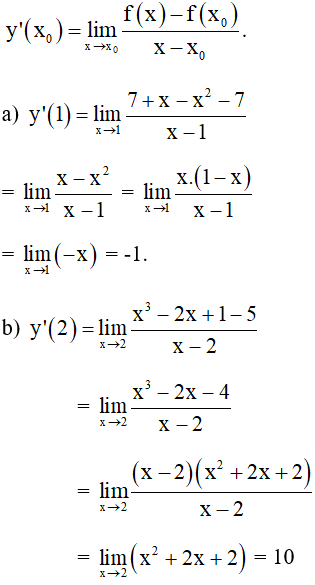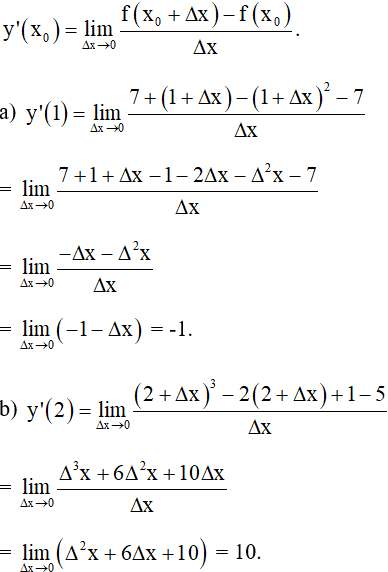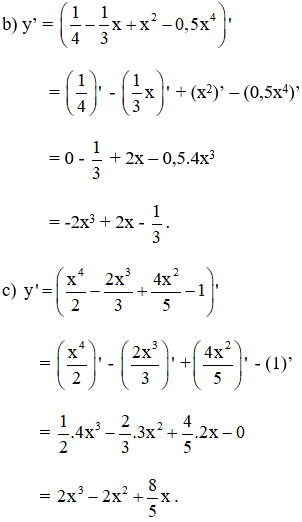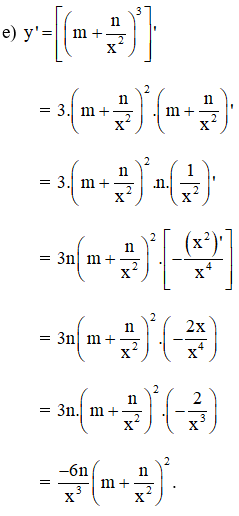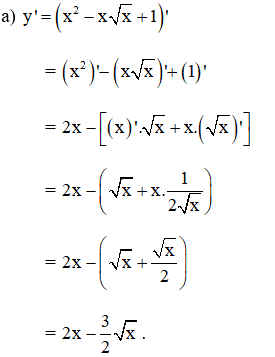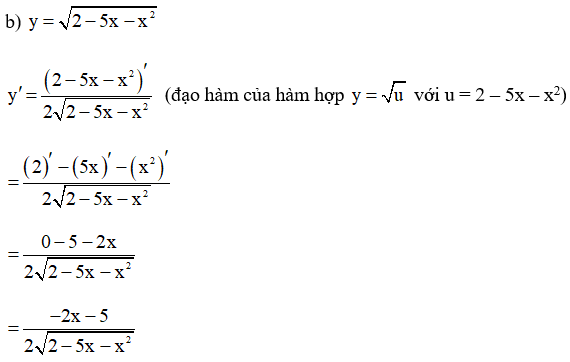10 câu hỏi trắc nghiệm thuộc Bài 2: Quy tắc tính đạo hàm

Câu 1:

Dùng định nghĩa tính đạo hàm của hàm số y = $x^{3}$ tại điểm x tùy ý.

Dự đoán đạo hàm của hàm số y = $x^{100}$ tại điểm x.

Xem đáp án

- Giả sử Δx là số gia của đối số tại x_o bất kỳ. Ta có:

- Dự đoán đạo hàm của y = x¹⁰⁰ tại điểm x là 100x⁹⁹

Câu 2:

Chứng minh khẳng định trong nhận xét trên.

a) Đạo hàm của hàm hằng bằng 0: c’ = 0.

b) Đạo hàm của hàm số y = x bằng 1: x’ = 1.

Xem đáp án

a) Hàm hằng ⇒ Δy = 0

b) theo định lí 1

y = x hay y = x¹ ⇒ y’= (x¹)’= 1. x^1-1 = 1. x^o = 1.1 =1

Câu 3:

Áp dụng các công thức trong Định lí 3, hãy tính đạo hàm của các hàm số

y = 5 $x^{3}$ - 2 $x^{5}$ ; $y = - x^{3} . \sqrt{x}$ .

Xem đáp án

Câu 4:

Trả lời câu hỏi Toán 11 Đại số Bài 2 trang 160: Hãy chứng minh các công thức trên và lấy ví dụ minh họa.

Xem đáp án

- Nếu k là một hằng số thì (ku)’ = ku’

Thật vậy, ta có: (ku)' = k'u + ku' = 0.u + ku' = ku'

Do đạo hàm của hàm hằng bằng 0

Câu 5:

Hàm số $y = \sqrt{x^{2} + x + 1}$ là hàm hợp của hàm số nào ?

Xem đáp án

Hàm số là hàm hợp của hàm số y = √u với u = x² + x + 1

Câu 6:

Bằng định nghĩa, tìm đạo hàm của các hàm số sau :

a. y = 7 + x – $x^{2}$ tại $x_{0}$ = 1

b. y = $x^{3}$ – 2x + 1 tại $x_{0}$ = 2.

Xem đáp án

Cách 1 : Áp dụng công thức

Cách 2 : Áp dụng công thức

Câu 7:

Tìm đạo hàm của các hàm số sau:

$a) y = x^{5} - 4 x^{3} + 2 x - 3$ ;

$b) y = \frac{1}{4} - \frac{1}{3} x + x^{2} - 0, 5 x^{4}$ ;

$c) y = \frac{x^{4}}{2} - \frac{2 x^{3}}{3} + \frac{4 x^{2}}{5} - 1$ ;

$d) y = 3 x^{5} (8 - 3 x^{2})$ .

Xem đáp án

a) y’ = (x⁵ – 4x³ + 2x – 3)’

= (x⁵)’ – (4x³)’ + (2x)’ – (3)’

= 5x⁴ – 4.3x² + 2

= 5x⁴ – 12x² + 2.

d) Cách 1 : y = 3x⁵ (8 - 3x²)

= 3x⁵.8 – 3x⁵.3x² = 24x⁵ – 9x⁷

⇒ y’ = (24x⁵ – 9x⁷)’

= (24x⁵)' – (9x⁷)’

= 24.5x⁴ – 9.7x⁶

= 120x⁴ – 63x⁶.

Cách 2 : Áp dụng công thức tính đạo hàm của tích :

⇒ y’ = [(3x⁵)’].(8 – 3x²) + 3x⁵.[(8 – 3x²)’]

= 3.5x⁴(8 – 3x²) + 3x⁵.[(8)’ – (3x²)’]

= 15x⁴(8 – 3x²) + 3x⁵.(0 – 3.2x)

= 15x⁴.8 – 15x⁴.3x² + 3x⁵.(-6x)

= 120x⁴ – 45x⁶ – 18x⁶

= 120x⁴ – 63x⁶.

Câu 8:

Tìm đạo hàm của các hàm số sau:

$a . y = {(x^{7} - 5 x^{2})}^{3}$

$b . y = (x^{2} + 1) (5 - 3 x^{2})$

$c . y = \frac{2 x}{x^{2} - 1}$

$d . y = \frac{3 - 5 x}{x^{2} - x + 1}$

$e . y = {(m + \frac{n}{x^{2}})}^{3} (m, n l à c á c h ằ n g s ố)$

Xem đáp án

a) Cách 1 :

y’ = [(x⁷ - 5x²)³]'

= [(x⁷)³ – 3.(x⁷)².5x² + 3.x⁷.(5x²)² – (5x²)³]’

= (x²¹ – 15.x¹⁶ + 75x¹¹ – 125x⁶)’

= (x²¹)’ – (15x¹⁶)’ + (75x¹¹)’ – (125x⁶)’

= 21x²⁰ – 15.16x¹⁵ + 75.11x¹⁰ – 125.6x⁵

= 21x²⁰ – 240x¹⁵ + 825x¹⁰ – 750x⁵.

Cách 2 :

y’ = [(x⁷ - 5x²)³]'

= 3.(x⁷ – 5x²)².(x⁷ – 5x²)’ (Đạo hàm của hàm hợp với u = x⁷ – 5x² ; y = u³)

= 3.(x⁷ – 5x²)².[ (x⁷)’ – (5x²)’]

= 3.(x⁷ – 5x²)²(7x⁶ – 5.2x)

= 3.(x⁷ – 5x²)²(7x⁶ – 10x)

b) y’ = [(x² + 1)(5 – 3x²)]’

= (x² + 1)’.(5 – 3x²) + (x² + 1)(5 – 3x²)’ (Đạo hàm của tích)

= [(x²)’ + (1)’](5 – 3x²) + (x² + 1)[(5)’ – (3x²)’]

= (2x + 0)(5 – 3x²) + (x² + 1)(0 – 3.2x)

= 2x.(5 – 3x²) + (x² + 1).(-6x)

= 2x.5 – 2x.3x² + x²(-6x) + 1(-6x)

= 10x – 6x³ – 6x³ – 6x

= -12x³ + 4x.

Câu 9:

Tính đạo hàm của các hàm số sau:

$a) y = x^{2} - x \sqrt{x} + 1$ ;

$b) y = \sqrt{2 - 5 x - x^{2}}$ ;

$c) y = \frac{x^{3}}{\sqrt{a^{2} - x^{2}}} (a l à h ằ n g s ố)$ ;

$d) y = \frac{1 + x}{\sqrt{1 - x}}$ .

Xem đáp án

(Đạo hàm của hàm hợp với u = 2 – 5x – x² và y = √u)

Câu 10:

Cho y= $x^{3}$ - $3 x^{2}$ +2. Tìm x để:

a. y' > 0

b. y' < 3

Xem đáp án

y = x³ – 3x² + 2.

⇒ y’ = (x³ – 3x² + 2)’

= (x³)’ – (3x²)’ + (2)’

= 3x² – 3.2x + 0

= 3x² – 6x.

a) y’ > 0

⇔ 3x² – 6x > 0

⇔ 3x(x – 2) > 0

⇔ x < 0 hoặc x > 2.

b) y’ < 3

⇔ 3x² – 6x < 3

⇔ 3x² – 6x – 3 < 0

⇔ 1- √2 < x < 1 + √2.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải SGK Toán 11 Chương 5: Đạo hàm

Bài 2: Quy tắc tính đạo hàm

Danh sách câu hỏi

Bài thi liên quan