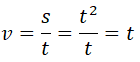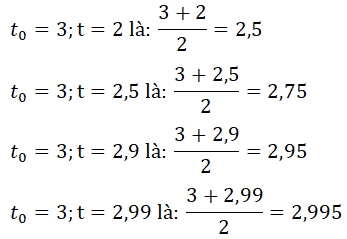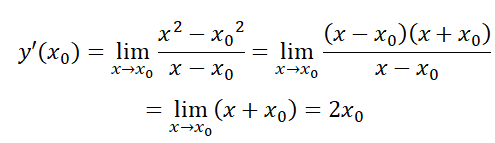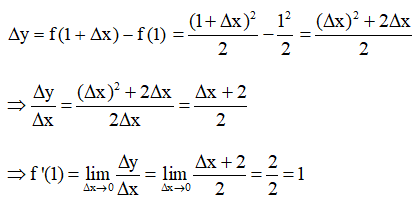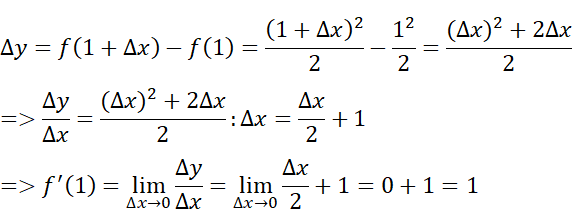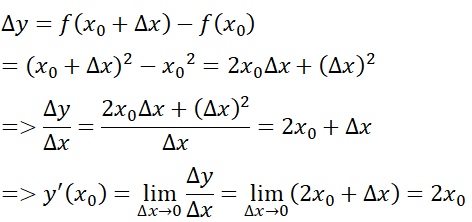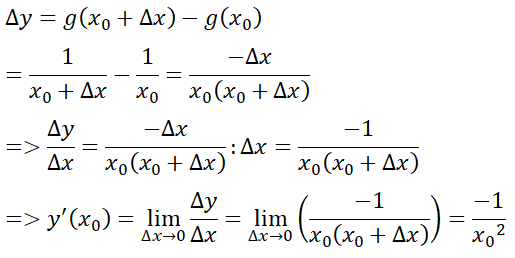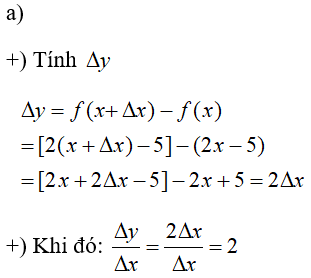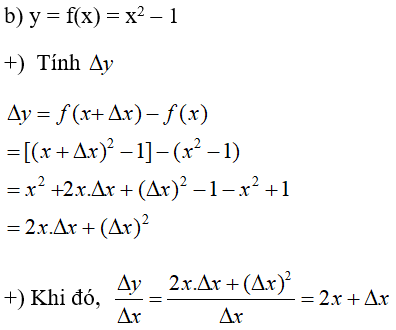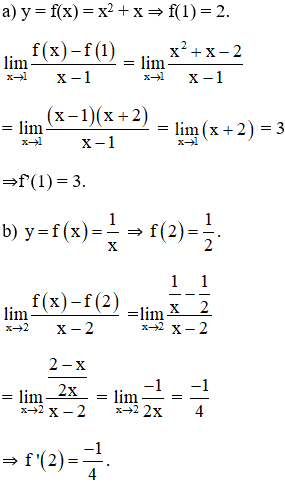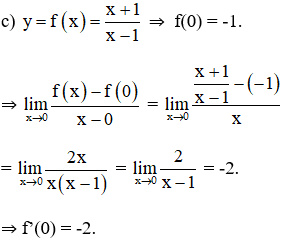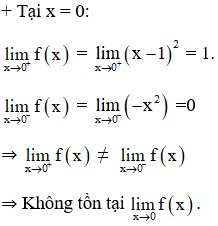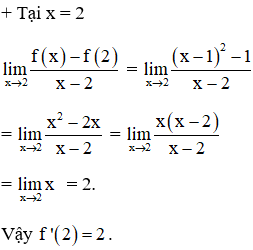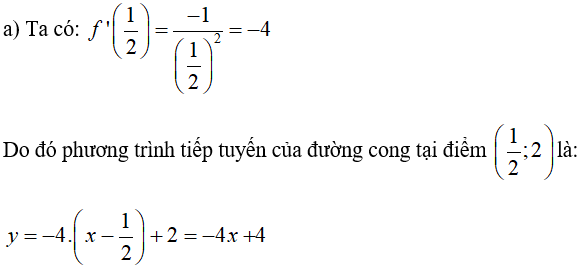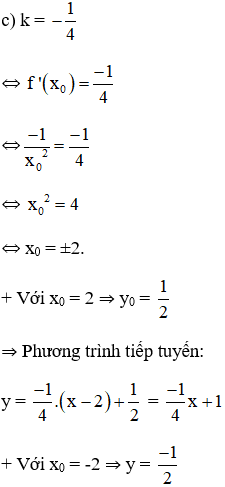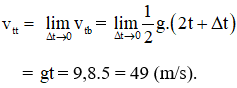12 câu hỏi trắc nghiệm thuộc Bài 1: Định nghĩa và ý nghĩa của đạo hàm

Câu 1:

Một đoàn tàu chuyển động khởi hành từ một nhà ga. Quãng đường s (mét) đi được của đoàn tàu là một hàm số của thời gian t (phút). Ở những phút đầu tiên, hàm số đó là s = t2.

Hãy tính vận tốc trung bình của chuyển động trong khoảng [t; to] với to = 3 và t = 2; t = 2,5; t = 2,9; t = 2,99.

Nêu nhận xét về những kết quả thu được khi t càng gần to = 3.

Xem đáp án

Vận tốc của đoàn tàu là:

Vận tốc trung bình của chuyển động trong khoảng [t; to] với:

t càng gần to = 3 thì vận tốc trung bình của chuyển động trong khoảng [t; to] càng gần 3

Câu 2:

Cho hàm số y = $x^{2}$ . Hãy tính y'(xo) bằng định nghĩa.

Xem đáp án

Câu 3:

a) Vẽ đồ thị của hàm số f(x) = $\frac{x^{2}}{2}$

b) Tính f’(1).

c) Vẽ đường thẳng đi qua điểm M(1; 1/2) và có hệ số góc bằng f’(1). Nêu nhận xét về vị trí tương đối của đường thẳng này và đồ thị hàm số đã cho.

Xem đáp án

- Giả sử Δx là số gia của đối số tại x_o = 1. Ta có:

- Đường thẳng có hệ số góc bằng f'(1) = 1 có dạng:

y = 1.x + a hay y = x + a

Mà đường thẳng đó đi qua điểm M(1;1/2) nên có: 1/2 = 1 + a ⇒ a = 1/2 - 1 = -1/2

⇒ đường thẳng đi qua M và có hệ số góc bằng 1 là: y = x – 1/2

Ta có đồ thị như trên. Đường thẳng y = x – 1/2 tiếp xúc với đồ thị hàm số f(x) tại M

Câu 4:

Viết phương trình đường thẳng đi qua Mo(xo; yo) và có hệ số góc λ

Xem đáp án

y = λ(x – x_o) + y_o hay y = λx + (–λx_o + y_o)

Câu 5:

Bằng định nghĩa, hãy tính đạo hàm của các hàm số:

a) f(x) = $x^{2}$ tại điểm x bất kì;

b) g(x) = 1/x tại điểm bất kì x ≠ 0

Xem đáp án

a)Giả sử Δx là số gia của đối số tại x_o bất kỳ. Ta có:

b)Giả sử Δx là số gia của đối số tại x_o bất kỳ. Ta có:

Câu 6:

Tìm số gia của hàm số f(x) = $x^{3}$ , biết rằng:

a. $x_{0}$ = 1; Δx = 1;

b. $x_{0}$ = 1; Δx = -0,1;

Xem đáp án

a. Δy = f(x₀ + Δx) – f(x₀) = f(1 + 1) – f(1) = f(2) – f(1) = 2³ – 1³ = 7

b. Δy = f(x₀ + Δx) – f(x₀) = f(1 – 0,1) – f(1) = f(0,9) – f(1) = (0,9)³ – 1³ = -0,271.

Câu 7:

Tính Δy và $\frac{∆ y}{∆ x}$ của các hàm số sau theo x và Δx:

a) $y = 2 x - 5$ ;

b) $y = x^{2} - 1$ ;

c) $y = 2 x^{3}$ ;

d) $y = \frac{1}{x}$ .

Xem đáp án

Gọi Δ x là số gia của biến số x.

Câu 8:

Tính (bằng định nghĩa) đạo hàm của mỗi hàm số tại các điểm đã chỉ ra:

$a) y = x^{2} + x t ạ i x_{0} = 1$

$b) y = \frac{1}{x} t ạ i x_{0} = 2$

$c) y = \frac{x + 1}{x - 1} t ạ i x_{0} = 0$

Xem đáp án

Câu 9:

Chứng minh rằng hàm số:

$f (x) = \{\begin{cases} {(x - 1)}^{2} (n ế u x \geq 0) \\ - x^{2} (n ế u x < 0) \end{cases}$

Không có đạo hàm tại điểm x = 0 nhưng có đạo hàm tại điểm x = 2.

Xem đáp án

⇒ Không tồn tại đạo hàm của f(x) tại x = 0.

Câu 10:

Viết phương trình tiếp tuyến đường cong y= $x^{3}$ .

a. Tại điểm (-1; -1);

b. Tại điểm có hoành độ bằng 2;

c. Biết hệ số góc của tiếp tuyến bằng 3.

Xem đáp án

Với mọi x0 ∈ R ta có:

a) Tiếp tuyến của y = x3 tại điểm (-1; -1) là:

y = f’(-1)(x + 1) + y(1)

= 3.(-1)2(x + 1) – 1

= 3.(x + 1) – 1

= 3x + 2.

b) x0 = 2

⇒ y0 = f(2) = 23 = 8;

⇒ f’(x0) = f’(2) = 3.22 = 12.

Vậy phương trình tiếp tuyến của y = x3 tại điểm có hoành độ bằng 2 là :

y = 12(x – 2) + 8 = 12x – 16.

c) k = 3

⇔ f’(x0) = 3

⇔ 3x02 = 3

⇔ x02 = 1

⇔ x0 = ±1.

+ Với x0 = 1 ⇒ y0 = 13 = 1

⇒ Phương trình tiếp tuyến : y = 3.(x – 1) + 1 = 3x – 2.

+ Với x0 = -1 ⇒ y0 = (-1)3 = -1

⇒ Phương trình tiếp tuyến : y = 3.(x + 1) – 1 = 3x + 2.

Vậy có hai phương trình tiếp tuyến của đường cong y = x3 có hệ số góc bằng 3 là y = 3x – 2 và y = 3x + 2.

Câu 11:

Viết phương trình tiếp tuyến của hypebol: $y = \frac{1}{x}$

a) Tại điểm $(\frac{1}{2}; 2)$ ;

b) Tại điểm có hoành độ bằng -1;

c) Biết rằng hệ số góc của tiếp tuyến bằng $\frac{- 1}{4}$ .

Xem đáp án

b) Tại x₀ = -1

⇒ y₀ = -1

⇒ f’(x₀) = -1.

Vậy phương trình tiếp tuyến của đường cong 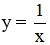tại điểm có hoành độ -1 là:

y = -1(x + 1) – 1 = -x – 2.

⇒ Phương trình tiếp tuyến:

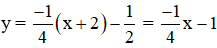
Giải bài 6 trang 156 sgk Đại Số 11 | Để học tốt Toán 11

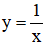
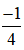
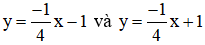
Vậy có hai phương trình tiếp tuyến của hypebol có hệ số góc bằng

Câu 12:

Bài 7 (trang 157 SGK Đại số 11): Một vật rơi tự do theo phương trình s = 1/2 $g t^{2}$ , trong đó g≈9,8m/ $s^{2}$ là gia tốc trọng trường.

a. Tìm vận tốc trung bình của chuyển động trong khoảng thời gian từ t (t = 5s) đến t + Δt, trong các trường hợp Δt=0,1s; Δt=0,05s; Δt=0,001s.

b. Tìm vận tốc tức thời của chuyển động tại thời điểm t = 5s.

Xem đáp án

a) Vận tốc trung bình trong khoảng thời gian từ t đến t + Δt là:

b) Vận tốc tức thời tại thời điểm t = 5s chính là vận tốc trung bình trong khoảng thời gian (t; t + Δt) khi Δt → 0 là :

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải SGK Toán 11 Chương 5: Đạo hàm

Bài 1: Định nghĩa và ý nghĩa của đạo hàm

Danh sách câu hỏi

Bài thi liên quan