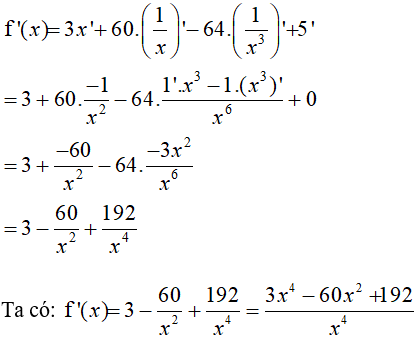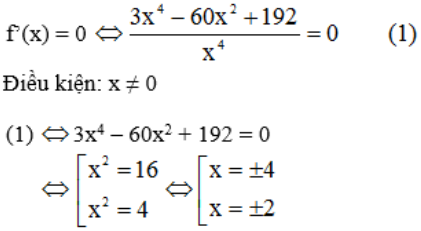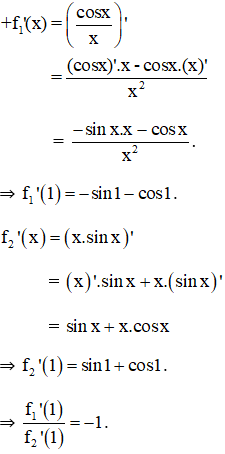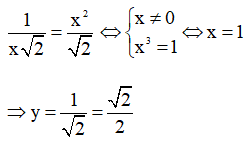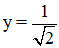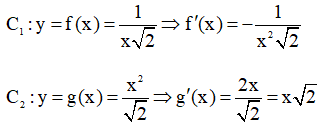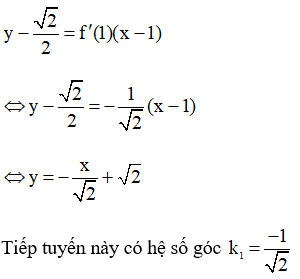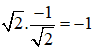13 câu hỏi trắc nghiệm thuộc Ôn tập chương 5

Câu 1:

Tìm các đạo hàm sau:

a) $y = \frac{x^{3}}{3} - \frac{x^{2}}{2} + x - 5$ ;

b) $y = \frac{2}{x} - \frac{4}{x^{2}} + \frac{5}{x^{3}} - \frac{6}{7 x^{4}}$ ;

c) $y = \frac{3 x^{2} - 6 x + 7}{4 x}$ ;

d) $y = (\frac{2}{x} + 3 x) (\sqrt{x} - 1)$ ;

e) $y = \frac{1 + \sqrt{x}}{1 - \sqrt{x}}$ ;

f) $y = \frac{- x^{2} + 7 x + 5}{x^{2} - 3 x}$ .

Xem đáp án

Câu 2:

Tìm đạo hàm của các hàm số sau:

a) $y = 2 \sqrt{x} . \sin x - \frac{\cos x}{x}$ ;

b) $y = \frac{3 \cos x}{2 x + 1}$ ;

c) $y = \frac{t^{2} + 2 \cos t}{\sin t}$ ;

d) $y = \frac{2 \cos φ - \sin φ}{3 \sin φ + \cos φ}$ ;

e) $y = \frac{\tan x}{\sin x + 2}$ ;

f) $y = \frac{c o t x}{2 \sqrt{x} - 1}$ .

Xem đáp án

Câu 3:

Cho hàm số: $f (x) = \sqrt{1 + x}$

Tính f(3) + (x - 3)f’(3)

Xem đáp án

Câu 4:

Cho hai hàm số f(x) = tan(x) và g(x) = $\frac{1}{1 - x}$ . Tính $\frac{f' (0)}{g' (0)}$

Xem đáp án

Câu 5:

Giải phương trình f'(x) = 0, biết rằng: $f (x) = 3 x + \frac{60}{x} - \frac{64}{x^{3}} + 5$ .

Xem đáp án

Câu 6:

Cho $f_{1} (x) = \frac{\cos x}{x}, f_{2} (x) = x \sin x .$

Tính $\frac{f_{1}' (1)}{f_{2}' (1)}$

Xem đáp án

Câu 7:

Viết phương trình tiếp tuyến của:

a) Hypebol $y = \frac{x + 1}{x - 1}$ tại điểm A(2; 3).

b) Đường cong y = x³ + 4x² – 1 tại điểm có hoành độ x₀ = -1.

c) Của parabol y = x²– 4x + 4 tại điểm có tung độ y₀ = 1.

Xem đáp án

Câu 8:

Cho chuyển động thẳng xác định bởi phương trình S = t³ – 3t² – 9t, trong đó t được tính bằng giây (s) và S được tính bằng mét (m).

a.Tính vận tốc của chuyển động khi t = 2s.

b.Tính gia tốc của chuyển động khi t = 3s.

c.Tính gia tốc tại thời điểm vận tốc triệt tiêu.

d.Tính vận tốc tại thời điểm gia tốc triệt tiêu.

Xem đáp án

Vận tốc: v(t) = S’(t) = (t³ – 3t² – 9t)' = 3t² – 6t – 9.

Gia tốc : a(t) = v’(t) = (3t² – 6t – 9)’ = 6t – 6.

a) Khi t = 2s, v(2) = 3.2² – 6.2 – 9 = -9 (m/s).

b) Khi t = 3s, a(3) = 6.3 – 6 = 12 (m/s²).

c) v(t) = 0 ⇔ 3t² – 6t – 9 = 0 ⇔ t = 3 (vì t > 0).

Khi đó a(3) = 12 m/s².

d) a(t) = 0 ⇔ 6t – 6 = 0 ⇔ t = 1.

Khi đó v(1) = 3.1² – 6.1 – 9 = -12 (m/s).

Câu 9:

Cho hai hàm số: $y = \frac{1}{x \sqrt{2}}$ và $y = \frac{x^{2}}{\sqrt{2}}$ .

Viết phương trình tiếp tuyến với đồ thị của mỗi hàm số đã cho tại giao điểm của chúng. Tính góc giữa hai tiếp tuyến kể trên.

Xem đáp án

Phương trình hoành độ giao điểm của hai hàm số là :

Thay x = 1 vào trong hai hàm số ta có

⇒ Tọa độ giao điểm

+ Góc giữa hai đường tiếp tuyến.

Tích hệ số góc của hai đường tiếp tuyến bằng:

⇒ Hai tiếp tuyến vuông góc với nhau

⇒ Góc giữa hai tiếp tuyến bằng 90º.

Câu 10:

Với $g (x) = \frac{x^{2} - 2 x + 5}{x - 1}; g' (2) =$

A. 1

B. -3

C. -5

D. 0

Xem đáp án

Chọn đáp án B.

Giải thích:

Câu 11:

Nếu $f (x) = \sin^{3} x + x^{2} t h ì f'' (\frac{- π}{2}) b ằ n g :$

A. 0

B. 1

C. -2

D. 5

Xem đáp án

Chọn đáp án D.

Giải thích:

f(x) = sin³x + x²

⇒ f'(x) = 3sin²x.(sinx)' + 2x = 3sin²x.cosx + 2x

⇒ f''(x) = (3sin²x.cosx)' + (2x)'

= 3(sin²x)'.cosx + 3sin²x(cosx)' + 2

= 3.2.sinx.cosx.cosx + 3sin²x.(-sinx) + 2

= 6sinx.cos²x - 3sin³x + 2

⇒ f''(-π/2) = 5

Câu 12:

Cho $h (x) = 5 {(x + 1)}^{3} + 4 (x + 1)$ .

Tập nghiệm của phương trình $h'' (x) = 0$ là:

A. [-1;2]

B. [- $\infty$ ;0]

C. {-1}

D. $\emptyset$

Xem đáp án

Chọn đáp án C.

Giải thích:

Ta có:

h'(x) = 15(x + 1)² + 4

h''(x) = 30(x + 1);

h"(x) = 0 ⇔ 30(x + 1) = 0 ⇔ x = -1

Câu 13:

Cho $f (x) = \frac{x^{3}}{3} + \frac{x^{2}}{2} + x$ .

Tập nghiệm của bất phương trình $f' (x) \leq 0$ là:

A. $\emptyset$

B. (0; $\infty$ )

C. [-2; 2]

D. ( $- \infty; \infty$ )

Xem đáp án

Chọn đáp án A.

Giải thích:

Ta có: f’(x) = x² + x + 1 = 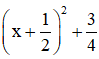> 0 với mọi x ∈ R.

Do đó phương trình f’(x) ≤ 0 vô nghiệm

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải SGK Toán 11 Chương 5: Đạo hàm

Ôn tập chương 5

Danh sách câu hỏi

Bài thi liên quan