Giải SGK Toán 11 Hình học - Chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
Bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song
-
2060 lượt thi
-
6 câu hỏi
-
40 phút
Danh sách câu hỏi
Câu 1:
Quan sát các cạnh tường trong lớp học và xem cạnh tường là hình ảnh của đường thẳng. Hãy chỉ ra một số cặp đường thẳng không thể cùng thuộc một mặt phẳng.
Xem đáp án
Học sinh tự quan sát
Câu 2:
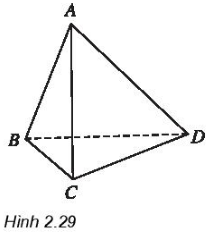
Cho tứ diện ABCD, chứng minh hai đường thẳng AB và CD chéo nhau. Chỉ ra cặp đường thẳng chéo nhau khác của tứ diện này (h.2.29).
Xem đáp án
Không tìm được mặt phẳng nào chứa AB và CD ⇒ AB và CD chéo nhau
Các cặp đường thẳng chéo nhau khác của tứ diện này: AC và BD, BC và A
Câu 3:
Cho hai mặt phẳng và . Một mặt phẳng cắt và lần lượt theo các giao tuyến a và b. Chứng minh rằng khi a và b cắt nhau tại I thì I là điểm chung của và . (h.2.32).
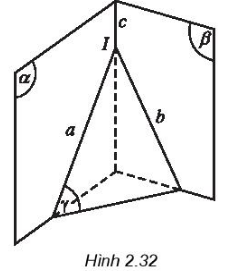
Xem đáp án
a và b cắt nhau tại I
(vì a là giao tuyến của α và λ)
( vì b là giao tuyến của β và λ)
Nên I là điểm chung của và
Câu 4:
Cho tứ diện ABCD. Gọi P, Q, R và S là bốn điểm lần lượt lấy trên bốn cạnh AB, BC, CD và DA. Chứng minh rằng nếu bốn điểm P, Q, R và S đồng phẳng thì:
a) Ba đường thẳng PQ, SR và AC hoặc song song hoặc đồng quy.
b) Ba đường thẳng PS, RQ và BD hoặc song song hoặc đồng quy.
Xem đáp án
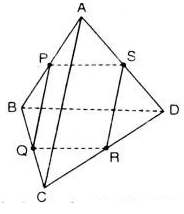
a) Ta có:
Vậy hoặc đồng qui hoặc song song.
b)
Vậy đồng quy hoặc song song.
Câu 5:
Cho tứ diện ABCD và ba điểm P, Q, R lần lượt lấy trên ba cạnh AB, CD, BC. Tìm giao điểm S của AD và mặt phẳng (PQR) trong hai trường hợp sau đây.
a) PR song song với AC;
b) PR cắt AC.
Xem đáp án
a) PR // AC
mp(PQR) và mp(ACD) lần lượt chứa hai đường thẳng song song PR // AC
⇒ (PQR) ∩ (ACD) = Qt là đường thẳng song song với AC và PR.
Gọi Qt ∩ AD = S
⇒ S = AD ∩ (PQR).
b) PR ∩ AC = I.
Có : Q ∈ (ACD) ∩ (PQR)
+ (ABC) ∩ (PQR) = PR.
+ (ACD) ∩ (ABC) = AC
+ (ACD) cắt (PQR)
⇒ PR; AC và giao tuyến của (ACD) và (PQR) đồng quy
Mà PR ∩ AC = I
⇒ I ∈ (ACD) ∩ (PQR).
⇒ (ACD) ∩ (PQR) = QI.
trong (ACD): QI ∩ AD = S chính là giao tuyến của (PQR) và AD.
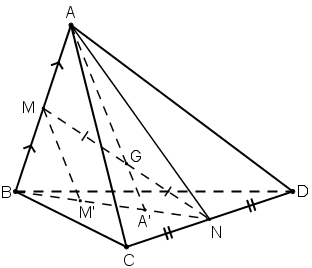
Câu 6:
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và G là trung điểm của đoạn MN.
a) Tìm giao điểm A’ của đường thẳng AG và mp(BCD).
b) Qua M kẻ đường thẳng Mx song song với AA’ và Mx cắt (BCD) tại M’.
c) Chứng minh GA = 3GA’
Xem đáp án
a) Có: MN ⊂ (ABN)
⇒ G ∈ (ABN)
⇒ AG ⊂ (ABN).
Trong (ABN), gọi A’ = AG ∩ BN.
⇒ A’ ∈ BN ⊂ (BCD)
⇒ A’ = AG ∩ (BCD).
b) + Mx // AA’ ⊂ (ABN) ; M ∈ (ABN)
⇒ Mx ⊂ (ABN).
M’ = Mx ∩ (BCD)
⇒ M’ nằm trên giao tuyến của (ABN) và (BCD) chính là đường thẳng BN.
⇒ B; M’; A’ thẳng hàng.
⇒ BM’ = M’A’ = A’N.
c) Áp dụng chứng minh câu b ta có:
ΔMM’N có: MM’ = 2.GA’
ΔBAA’ có: AA’ = 2.MM’
⇒ AA’ = 4.GA’
⇒ GA = 3.GA’.