Giải SGK Toán 11 Hình học - Chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
Bài 5: Phép chiếu song song. Hình biểu diễn của một hình không gian
-
2061 lượt thi
-
6 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Hình chiếu song song của một hình vuông có thể là hình bình hành được không?
Xem đáp án
Hình chiếu song song của một hình vuông có thể là hình bình hành
Câu 2:
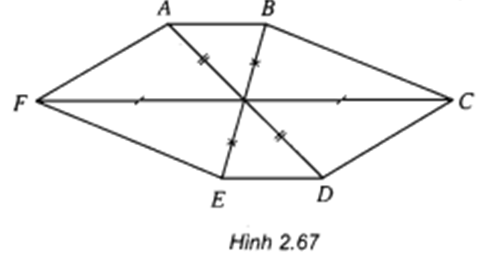
Hình 2.67 có thế là hình chiếu song song của hình lục giác đều được không? Vì sao?
Xem đáp án
Hình 2.67 không thể là hình chiếu song song của hình lục giác đều vì
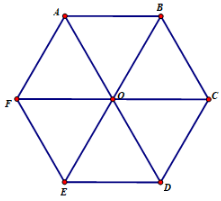
Lục giác đều ABCDEF có O là giao điểm các đường chéo
Ta có: AO // BC
Trên hình 2.67 không biểu diễn được điều đó
(Phép chiếu song song biến hai đường thằng song song thành hai đường thẳng song song hoặc trùng nhau)
Câu 3:
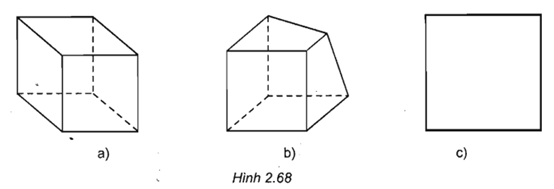
Trong các hình 2.68, hình nào biểu diễn cho hình lập phương?
Xem đáp án
Hình a biểu diễn hình lập phương
Câu 4:
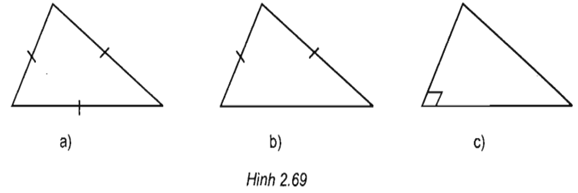
Các hình 2.69a, 2.69c, 2.69c là hình biểu diễn của tam giác nào?
Xem đáp án
Hình 2.69a là hình biểu diễn của tam giác đều
Hình 2.69b là hình biểu diễn của tam giác cân
Hình 2.69c là hình biểu diễn của tam giác vuông
Câu 5:
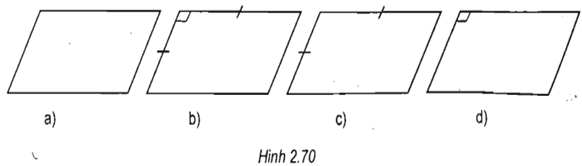
Các hình 2.70a, 2.70b, 2.70c, 2.70d là hình biểu diễn của các hình bình hành nào (hình bình hành, hình thoi, hình vuông, hình chữ nhật)?
Xem đáp án
Hình 2.70a biểu diễn hình bình hành
Hình 2.70b biểu diễn hình vuông
Hình 2.70c biểu diễn hình thoi
Hình 2.70d biểu diễn hình chữ nhật
Câu 6:
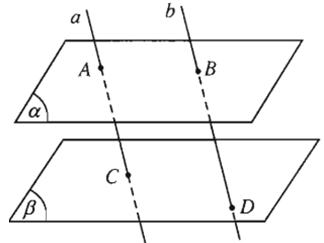
Cho hai mặt phẳng và song song với nhau. Đường thẳng a cắt và lần lượt tại A và C. Đường thẳng b song song với a cắt và lần lượt tại B và D.
Hình 2.72 minh họa nội dung trên đúng hay sai?
Xem đáp án
Sai vì
Ta có định lí 3 trang 67: cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song
Theo đề bài ta có:
a//b nên A,B,C,D thuộc mặt phẳng
AB là giao tuyến của và (ABDC)
CD là giao tuyến của và (ABDC)
⇒ AB // CD (theo định lí)
Hình 2.72 không biểu diễn được AB // CD