Giải SGK Toán 11 Hình học - Chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
Câu hỏi ôn tập chương 2
-
2331 lượt thi
-
7 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Hãy nêu các cách xác định mặt phẳng, kí hiệu mặt phẳng.
 Xem đáp án
Xem đáp án
Có 3 cách xác định mặt phẳng
– Một mặt phẳng được xác định khi biết ba điểm không thẳng hàng của nó.
– Một mặt phẳng được xác định khi biết một đường thẳng và một điểm nằm ngoài đường thẳng.
– Một mặt phẳng được xác định khi biết hai đường thẳng cắt nhau thuộc mặt phẳng.
Ngoài ra, từ định nghĩa của hai đường thẳng song song trong không gian ta còn có cách xác định.
– Hai đường thẳng song song xác định một mặt phẳng
Câu 2:
Thế nào là đường thẳng song song với đường thẳng, đường thẳng song song với mặt phẳng, mặt phẳng song song với mặt phẳng.
 Xem đáp án
Xem đáp án
- Đường thẳng song song với đường thẳng nếu chúng không có điểm chung và chúng cùng nằm trên cùng mặt phẳng.
- Đường thẳng song song với mặt phẳng nếu chúng không có điểm chung.
- Mặt phẳng song song với mặt phẳng nếu chúng không có điểm chung.
Câu 3:
Nêu phương pháp chứng minh ba điểm thẳng hàng.
 Xem đáp án
Xem đáp án
Muốn chứng minh ba điểm thẳng hàng ta chứng minh ba điểm đó là ba điểm chung của hai mặt phẳng phân biệt.
Câu 4:
Nêu phương pháp chứng minh ba đường thẳng đồng quy.
 Xem đáp án
Xem đáp án
Để chứng minh ba đường thẳng đồng quy, ta chứng minh:
– Ba đường thẳng ấy không đồng phẳng và đôi một cắt nhau.
– Ba đường thẳng ấy là các giao tuyến của ba mặt phẳng phân biệt đôi một cắt nhau và chúng không song song.
Câu 5:
Nêu phương pháp chứng minh.
- Đường thẳng song song với đường thẳng;
- Đường thẳng song song với mặt phẳng;
- Mặt phẳng song song với mặt phẳng.
 Xem đáp án
Xem đáp án
a) Chứng minh đường thẳng song song với đường thẳng:
Để chứng minh hai đường thẳng song song, ta sử dụng các định lí.
- Ba mặt phẳng phân biệt đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng qui hoặc đôi một song song với nhau.
- Hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
- Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.
- Cho đường thẳng d song song với mặt phẳng Nếu mặt phẳng chứa d và cắt theo giao tuyến d’ thì d’ song song với d.
- Hai mặt phẳng phân biệt cùng song song với với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.
- Một mặt phẳng cắt hai mặt phẳng song song cho hai giao tuyến song song.
- Sử dụng các phương pháp của hình học phẳng. Tính chất đường trung bình, định lí Ta-lét đảo, cạnh đối hình bình hành…
- Sử dụng tính chất về cạnh bên, cạnh đáy của hình lăng trụ.
b) Chứng minh đường thẳng song song với mặt phẳng
- Chứng minh d song song với đường thẳng d’ nằm trong và d không thuộc
- Có hai mặt phẳng song song, bất kì đường nào nằm trong hai mặt phẳng này cũng song song với mặt phẳng kia.
c) Chứng minh mặt phẳng song song với mặt phẳng
- Chứng minh mặt phẳng này chứa hai đường thẳng cắt nhau song song với mặt phẳng kia.
- Chứng minh hai mặt phẳng đó cùng song song với mặt phẳng thứ ba.
Câu 6:
Phát biểu định lí Ta – lét trong không gian.
 Xem đáp án
Xem đáp án
Định lí Ta – lét trong không gian:
- Định lí thuận (Định lí Ta – lét)
Ba mặt phẳng đôi một song song chắn trên hai cát tuyến bất kì các đoạn thẳng tương ứng tỉ lệ, nghĩa là:
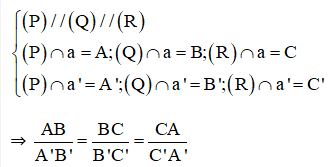
- Định lí đảo (Định lí Ta – lét đảo)
Giả sử trên hai đường thẳng a và a' lần lượt lấy hai bộ ba điểm (A, B, C) và (A', B', C') sao cho AB/A'B'= BC/B'C' = CA/C'A'
Khi đó ba đường thẳng AA', BB', CC' cùng song song với một mặt phẳng, nghĩa là ba đường thẳng đó nằm trên ba mặt phẳng song song với nhau.
Câu 7:
Nêu cách xác định thiết diện được tạo bởi một mặt phẳng với một hình chóp, hình hộp, hình lăng trụ.
 Xem đáp án
Xem đáp án
Để dựng thiết diện tạo bởi một mặt phẳng với hình chóp, hình hộp, hình lăng trụ, điều quan trọng là ta phải xác định các giao tuyến của mặt phẳng ấy với các mặt của hình chóp, hình hộp, hình lăng trụ
- Trước hết, ta cũng cần tìm giao điểm của các cạnh của hình chóp, hình hộp, hình lăng trụ
- Các đoạn thẳng nối các giao điểm ấy chính là các cạnh của thiết diện
- Ngoài ra cần sử dụng các kiến thức về quan hệ song song để giúp cho việc xác định các giao tuyến được chính xác và nhanh gọn.
