20 câu hỏi trắc nghiệm thuộc Mối quan hệ giữa hai đường thẳng - hamchoi.vn

Mối quan hệ giữa hai đường thẳng

Đề số 1

Mối quan hệ giữa hai đường thẳng

383 lượt thi
20 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho d,d′ là các đường thẳng có VTCP lần lượt là $\vec{u}, \vec{u'}, M \in d, M' \in d' .$ Khi đó $d \equiv d'$ nếu:

A $[\vec{u}, \vec{u^{'}}] = \vec{0}$

B. $[\vec{u}, \vec{u^{'}}] = [\vec{u}, \vec{M M^{'}}]$

C. $[\vec{u}, \vec{u^{'}}] = [\vec{u}, \vec{M M^{'}}] = \vec{0}$

D. $[\vec{u}, \vec{u^{'}}] \neq [\vec{u}, \vec{M M^{'}}]$

$d \equiv d^{'} \Leftrightarrow \vec{u}, \vec{u^{'}}, \vec{M M^{'}}$ đôi một cùng phương $\Leftrightarrow [\vec{u}, \vec{u^{'}}] = [\vec{u}, \vec{M M^{'}}] = \vec{0}$

Đáp án cần chọn là: C

Câu 2:

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng $d_{1} : \{\begin{matrix} x = - 1 + 3 t \\ y = - t \\ z = 1 - 2 t \end{matrix}$ và $d_{2} : \frac{x - 1}{- 3} = \frac{y - 2}{1} = \frac{z - 3}{2} .$

Vị trí tương đối của $d_{1}$ và $d_{2}$ là:

A.Song song.

B.Trùng nhau.

C.Cắt nhau.

D.Chéo nhau.

Đường thẳng $d_{1}$ đi qua $M_{1} (- 1; 0; 1)$ và có VTCP $\vec{u_{1}} = (3; - 1; - 2)$

Đường thẳng $d_{2}$ đi qua $M_{2} (1; 2; 3)$ và có VTCP $\vec{u_{2}} = (- 3; 1; 2)$

Ta có $\frac{3}{- 3} = \frac{- 1}{1} = \frac{- 2}{2}$ nên $\vec{u_{1}} ∥ \vec{u_{2}} (1)$

$\frac{- 1 - 1}{- 3} \neq \frac{0 - 2}{1} \neq \frac{1 - 3}{2}$ nên $M_{1} \notin d_{2} (2)$
Từ (1) và (2), suy ra d1 và d2 song song.

Đáp án cần chọn là: A

Câu 3:

Điều kiện cần và đủ để hai đường thẳng cắt nhau là:

A. $\{\begin{matrix} [\vec{u}, \vec{u^{'}}] \neq \vec{0} \\ [\vec{u}, \vec{u^{'}}] \vec{M M^{'}} = 0 \end{matrix}$

B. $[\vec{u}, \vec{u^{'}}] \neq \vec{0}$

C. $[\vec{u}, \vec{u^{'}}] \vec{M M^{'}} = 0$

D. $[\vec{u}, \vec{u^{'}}] = \vec{0}$

d cắt $d^{'} \Leftrightarrow \vec{u}, \vec{u^{'}}$ không cùng phương và $\vec{u}, \vec{u^{'}}, \vec{M M^{'}}$ đồng phẳng

$\Leftrightarrow \{\begin{matrix} [\vec{u}, \vec{u^{'}}] \neq \vec{0} \\ [\vec{u}, \vec{u^{'}}] \vec{M M^{'}} = 0 \end{matrix}$

Đáp án cần chọn là: A

Câu 4:

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng $d_{1} : \frac{x - 3}{1} = \frac{y - 2}{2} = \frac{z - 1}{1}$ và $d_{2} : \{\begin{matrix} x = t \\ y = 2 \\ z = 2 + t \end{matrix}$ .

Vị trí tương đối của d₁ và d₂ là:

A.Song song.

B.Trùng nhau.

C.Cắt nhau.

D.Chéo nhau.

Đường thẳng d₁ đi qua M₁(3;2;1) và có VTCP $\vec{u_{1}} = (1; 2; 1)$

Đường thẳng d₂ đi qua $M_{2} (0; 2; 2)$ và có VTCP $\vec{u_{2}} = (1; 0; 1)$

Ta có $[\vec{u_{1}}, \vec{u_{2}}] = (2; 0; - 2), \vec{M_{1} M_{2}} = (- 3; 0; 1)$

Suy ra $[\vec{u_{1}}, \vec{u_{2}}] . \vec{M_{1} M_{2}} = - 6 + 0 - 2 = - 8 \neq 0$
Do đó d1 và d2 chéo nhau.

Đáp án cần chọn là: D

Câu 5:

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng $d : \{\begin{matrix} x = - 1 + 2 t \\ y = - t \\ z = - 2 - t \end{matrix}$ . Trong các đường thẳng sau, đường thẳng nào vuông góc với d?

A. $d_{1} : \{\begin{matrix} x = 3 t \\ y = 1 + t \\ z = 5 t \end{matrix}$

B. $d_{2} : \{\begin{matrix} x = 2 \\ y = 2 + t \\ z = 1 + t \end{matrix}$

C. $d_{3} : \frac{x - 2}{3} = \frac{y}{2} = \frac{z - 1}{- 5}$

D. $d_{4} : \frac{x + 2}{2} = \frac{y}{- 1} = \frac{z + 1}{2}$

Đường thẳng d1 có VTCP ${\vec{u}}_{_{1}} = (3; 1; 5)$ , đường thẳng d có VTCP ${\vec{u}}_{_{d}} = (2; - 1; - 1)$

Vì ${\vec{u}}_{_{d}} . {\vec{u}}_{_{1}} = 3.2 - 1.1 - 5.1 = 0$

Đáp án cần chọn là: A

Câu 6:

Công thức tính khoảng cách từ điểm A đến đường thẳng d′ đi qua điểm M′ và có VTCP $\vec{u'}$ là:

A. $d (A, d^{'}) = \frac{|[\vec{A M^{'}}, \vec{u^{'}}]|}{|\vec{u^{'}}|}$

B. $d (A, d^{'}) = \frac{|[\vec{A M^{'}}, \vec{u^{'}}]|}{\vec{u^{'}}}$

C. $d (A, d^{'}) = \frac{[\vec{A M^{'}}, \vec{u^{'}}]}{\vec{u^{'}}}$

D. $d (A, d^{'}) = \frac{|\vec{A M^{'}} . \vec{u^{'}}|}{|\vec{u^{'}}|}$

Khoảng cách từ điểm A đến đường thẳng d′ được tính theo công thức

$d (A, d^{'}) = \frac{|[\vec{A M^{'}}, \vec{u^{'}}]|}{|\vec{u^{'}}|}$

Đáp án cần chọn là: A

Câu 7:

Góc giữa hai đường thẳng có các VTCP lần lượt là $\vec{u}, \vec{u^{'}}$ thỏa mãn:

A. $\cos φ = \frac{|\vec{u} . \vec{u^{'}}|}{|\vec{u}| . |\vec{u^{'}}|}$

B. $\cos φ = \frac{\vec{u} . \vec{u^{'}}}{|\vec{u}| . |\vec{u^{'}}|}$

C. $\cos φ = - \frac{\vec{u} . \vec{u^{'}}}{|\vec{u}| . |\vec{u^{'}}|}$

D. $\cos φ = - \frac{|\vec{u} . \vec{u^{'}}|}{|\vec{u}| . |\vec{u^{'}}|}$

Góc giữa hai đường thẳng có các VTCP lần lượt là $\vec{u}, \vec{u^{'}}$

$\cos φ = |\cos (\vec{u}, \vec{u^{'}})| = \frac{|\vec{u} . \vec{u^{'}}|}{|\vec{u}| . |\vec{u^{'}}|}$

Đáp án cần chọn là: A

Câu 8:

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình $\frac{x - 1}{3} = \frac{y + 2}{2} = \frac{z - 3}{- 4}$ và $d' : \frac{x + 1}{4} = \frac{y}{1} = \frac{z + 1}{2}$ . Điểm nào sau đây không thuộc đường thẳng d nhưng thuộc đường thẳng d′?

A.N(4;0;−1)

B.M(1;−2;3).

C.P(7;2;1) .

D.Q(7;2;3)

A: $\frac{4 - 1}{3} = \frac{0 + 2}{2} = \frac{- 1 - 3}{- 4} = 1 \Rightarrow N \in d$

B: $\frac{1 - 1}{3} = \frac{- 2 + 2}{2} = \frac{3 - 3}{- 4} = 0 \Rightarrow M \in d$

C: $\frac{7 - 1}{3} = \frac{2 + 2}{2} \neq \frac{1 - 3}{- 4} \Rightarrow P \notin d$ và $\frac{7 + 1}{4} = \frac{2}{1} \neq \frac{1 + 1}{2} \Rightarrow P \notin d^{'}$

D: $\frac{7 - 1}{3} = \frac{2 + 2}{2} \neq \frac{3 - 3}{- 4} \Rightarrow Q \notin d$ và $\frac{7 + 1}{4} = \frac{2}{1} = \frac{3 + 1}{2} \Rightarrow Q \in d^{'}$

Đáp án cần chọn là: D

Câu 9:

Giao điểm của hai đường thẳng

d : \{\begin{matrix} x = - 3 + 2 t \\ y = - 2 + 3 t \\ z = 6 + 4 t \end{matrix}

d' : \{\begin{matrix} x = 5 + t' \\ y = - 1 - 4 t' \\ z = 20 + t' \end{matrix}

có tọa độ là

A.(5;−1;20)

B.(3;−2;1)

C.(3;7;18)

D.(−3;−2;6)

Gọi $M = d \cap d^{'};$ do $M \in d \Rightarrow M (- 3 + 2 t; - 2 + 3 t; 6 + 4 t)$

$M \in d' \Rightarrow \{\begin{matrix} - 3 + 2 t = 5 + t' \\ - 2 + 3 t = - 1 - 4 t' \\ 6 + 4 t = 20 + t' \end{matrix} \Leftrightarrow \{\begin{matrix} t = 3 \\ t' = 2 \end{matrix} \Rightarrow M (3; 7; 18)$

Đáp án cần chọn là: C

Câu 10:

Trong không gian với hệ tọa độ Oxyz, cho các điểm A(0;0;2), B(1;0;0), C(2;2;0) và D(0;m;0). Điều kiện cần và đủ của m để khoảng cách giữa hai đường thẳng AB và CD bằng 2 là:

A $[\begin{matrix} m = 4 \\ m = - 2 \end{matrix}$

B. $[\begin{matrix} m = - 4 \\ m = 2 \end{matrix}$

C. $[\begin{matrix} m = 4 \\ m = 2 \end{matrix}$

D. $[\begin{matrix} m = - 4 \\ m = - 2 \end{matrix}$

Ta có $\vec{A B} = (1; 0; - 2), \vec{C D} = (- 2; m - 2; 0)$ và $\vec{A C} = (2; 2; - 2)$

Suy ra $[\vec{A B}; \vec{C D}] = (2 m - 4; 4; m - 2)$

Do đó

$d [A B, C D] = \frac{|[\vec{A B}; \vec{C D}] . \vec{A C}|}{|[\vec{A B}; \vec{C D}]|} \Leftrightarrow \frac{|2 (2 m - 4) + 8 - 2 (m - 2)|}{\sqrt{{(2 m - 4)}^{2} + 4^{2} + {(m - 2)}^{2}}} = 2$

$\Leftrightarrow | 2 m + 4 | = 2 \sqrt{5 m^{2} - 20 m + 36} \Leftrightarrow [\begin{matrix} m = 4 \\ m = 2 \end{matrix}$

Đáp án cần chọn là: C

Câu 11:

Trong không gian với hệ toạ độ Oxyz, cho đường thẳng $d : \frac{x - 3}{2} = \frac{y + 1}{1} = \frac{z - 1}{2}$ và điểm M(1;2;−3). Toạ độ hình chiếu vuông góc của điểm M lên đường thẳng d là

A.M′(1;2;−1)

B.M′(1;−2;1)

C.M′(1;−2;−1)

D.M′(1;2;1)

Gọi M′ là hình chiếu của M trên d.

d có vectơ chỉ phương ${\vec{u}}_{d} = (2; 1; 2)$

$M^{'} (3 + 2 t; - 1 + t; 1 + 2 t) \Rightarrow \vec{M M^{'}} = (2 + 2 t; - 3 + t; 4 + 2 t)$

Ta có $M M^{'} ⊥ d$ nên

$\vec{M M^{'}} . {\vec{u}}_{d} = 0 \Leftrightarrow (2 + 2 t) .2 + (- 3 + t) .1 + (4 + 2 t) .2 = 0 \Leftrightarrow 9 t + 9 = 0 \Leftrightarrow t = - 1$

$\Rightarrow M^{'} (1; - 2; - 1)$
Đáp án cần chọn là: C

Câu 12:

Trong không gian với hệ tọa độ Oxyz, cho 2 đường thẳng $d : \frac{x - 2}{- 3} = \frac{y + 2}{1} = \frac{z + 1}{- 2}$ và $d' : \frac{x}{6} = \frac{y - 4}{- 2} = \frac{z - 2}{4}$ . Mệnh đề nào sau đây là đúng?

A.d//d′.

B. $d \equiv d' .$

C.d và d′ cắt nhau.

D.d và d′ chéo nhau.

Ta có:

$\begin{array}{l} \vec{u_{d}} (- 3; 1; - 2); \vec{u_{d^{'}}} (6; - 2; 4) \Rightarrow \vec{u_{d^{'}}} = - 2 \vec{u_{d}} \\ A (2; - 2; - 1) \in d; \notin d^{'} \\ \Rightarrow d / / d^{'} \end{array}$

Đáp án cần chọn là: A

Câu 13:

Trong không gian Oxyz cho điểm A(1;1;−2) và đường thẳng $d : \frac{x - 1}{2} = \frac{y + 1}{1} = \frac{z}{- 2}$ . Đường thẳng qua A và song song với d có phương trình tham số là

A. $\{\begin{matrix} x = 1 + 2 t \\ y = 1 - t \\ z = - 2 - 2 t \end{matrix}$

B. $\{\begin{matrix} x = 1 + 2 t \\ y = 1 + t \\ z = - 2 - 2 t \end{matrix}$

C. $\{\begin{matrix} x = 1 + 2 t \\ y = 1 + t \\ z = 2 - 2 t \end{matrix}$

D. $\{\begin{matrix} x = 1 + 2 t \\ y = 1 + t \\ z = - 2 - 2 t \end{matrix}$

Đường thẳng $d : \frac{x - 1}{2} = \frac{y + 1}{1} = \frac{z}{- 2}$ có 1 VTCP là $\vec{u_{d}} = (2; 1; - 2)$ đây cũng là VTCP của đường thẳng đi qua A và song song với d.

Đường thẳng qua A và song song với d nhận $\vec{u} = (2; 1; - 2)$ là VTCP, có phương trình tham số: $\{\begin{matrix} x = 1 + 2 t \\ y = 1 + t \\ z = - 2 - 2 t \end{matrix}$

Đáp án cần chọn là: B

Câu 14:

Trong không gian Oxyz, cho đường thẳng $d : \{\begin{matrix} x = 1 + t \\ y = 2 - t \\ z = 1 - 3 t \end{matrix}$ . Đường thẳng Δ đi qua gốc tọa độ O, vuông góc với trục hoành Ox và vuông góc với đường thẳng d có phương trình là:

A. $Δ : \{\begin{matrix} x = 0 \\ y = - 3 t \\ z = - t \end{matrix}$

B. $Δ : \{\begin{matrix} x = t \\ y = - 3 t \\ z = t \end{matrix}$

C. $Δ : \{\begin{matrix} x = t \\ y = - 3 t \\ z = - t \end{matrix}$

D. $Δ : \{\begin{matrix} x = 0 \\ y = - 3 t \\ z = t \end{matrix}$

Đường thẳng $d : \{\begin{matrix} x = 1 + t \\ y = 2 - t \\ z = 1 - 3 t \end{matrix}$ có 1 VTCP là $\vec{u_{d}} = (1; - 1; - 3)$ , trục Ox có 1 VTCP là $\vec{i} = (1; 0; 0)$

Gọi $\vec{u_{Δ}}$ là 1 VTCP của đường thẳng $Δ$ , ta có

$\{\begin{matrix} Δ ⊥ O x \\ Δ ⊥ d \end{matrix} \Rightarrow \{\begin{matrix} \vec{u_{Δ}} . \vec{i} = 0 \\ \vec{u_{Δ}} . \vec{u_{d}} = 0 \end{matrix} \Rightarrow \vec{u_{Δ}} = [\vec{i}; \vec{u_{d}}] = (0; - 3; 1)$

Vậy phương trình đường thẳng $Δ$ đi qua O(0;0;0) và có 1 VTCP $\vec{u_{Δ}} = (0; - 3; 1)$ là:

$Δ : \{\begin{matrix} x = 0 \\ y = - 3 t \\ z = t \end{matrix}$

Đáp án cần chọn là: D

Câu 15:

Cho hai điểm A(1;−2;0),B(0;1;1), độ dài đường cao OH của tam giác OAB là:

A. $3 \sqrt{19}$

B. $\frac{3 \sqrt{19}}{13}$

C. $\sqrt{6}$

D. $\frac{\sqrt{66}}{11}$

Ta có: $\vec{O A} = (1; - 2; 0), \vec{A B} = (- 1; 3; 1)$

$\Rightarrow [\vec{O A}, \vec{A B}] = (|\begin{matrix} \begin{array}{l} - 2 \\ 3 \end{array} & \begin{array}{l} 0 \\ 1 \end{array} \end{matrix}|; |\begin{matrix} \begin{array}{l} 0 \\ 1 \end{array} & \begin{array}{l} 1 \\ - 1 \end{array} \end{matrix}|; |\begin{matrix} \begin{array}{l} 1 \\ - 1 \end{array} & \begin{array}{l} - 2 \\ 3 \end{array} \end{matrix}|) = (- 2; - 1; 1)$

Do đó $O H = d (O, A B) = \frac{|[\vec{O A}, \vec{A B}]|}{|\vec{A B}|} = \frac{\sqrt{2^{2} + 1^{2} + 1^{2}}}{\sqrt{1^{2} + 3^{2} + 1^{2}}} = \frac{\sqrt{66}}{11}$

Đáp án cần chọn là: D

Câu 16:

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng $d_{1} : \{\begin{matrix} x = 1 + t \\ y = 0 \\ z = - 5 + t \end{matrix}$ và $d_{2} : \{\begin{matrix} x = 0 \\ y = 4 - 2 t' \\ z = 5 + 3 t' \end{matrix}$ Phương trình đường vuông góc chung của d₁ và d₂ là:

A. $\frac{x - 4}{2} = \frac{y}{- 3} = \frac{z - 2}{- 2}$

B. $\{\begin{matrix} x = 4 - t \\ y = 3 t \\ z = - 2 + t \end{matrix}$

C. $\frac{x + 4}{- 2} = \frac{y}{3} = \frac{z - 2}{2}$

D. $\frac{x - 4}{- 2} = \frac{y}{3} = \frac{z + 2}{2}$

Gọi $M (1 + t; 0; t - 5) \in d_{1}, N (0; 4 - 2 t^{'}; 5 + 3 t^{'}) \in d_{2}$

Suy ra $\vec{M N} = (- 1 - t; 4 - 2 t^{'}; 10 + 3 t^{'} - t)$

Đường thẳng $d_{1}$ có VTCP $\vec{a} = (1; 0; 1), d_{2}$ có VTCP $\vec{b} = (0; - 2; 3)$

Để MN là đoạn vuông góc chung thì

$\{\begin{matrix} \vec{M N} . \vec{a} = 0 \\ \vec{M N} . \vec{b} = 0 \end{matrix} \Leftrightarrow \{\begin{matrix} t = 3 \\ t' = - 1 \end{matrix} \Rightarrow [\begin{matrix} M (4; 0; - 2) \\ N (0; 6; 2) \end{matrix}$

Phương trình đường vuông góc chung là $M N : \frac{x - 4}{- 2} = \frac{y}{3} = \frac{z + 2}{2}$

Đáp án cần chọn là: D

Câu 17:

Cho hình lập phương A(0;0;0),B(1;0;0),D(0;1;0),A′(0;0;1). Gọi M,N lần lượt là trung điểm của AB,CD. Khoảng cách giữa MN và A′C là:

A. $\frac{1}{\sqrt{2}}$

B. $\frac{\sqrt{2}}{4}$

C. $\frac{1}{2}$

D. $\frac{3}{\sqrt{2}}$

Gọi C(x;y;z) ta có:

$\vec{A B} = \vec{D C} \Leftrightarrow \{\begin{matrix} 1 - 0 = x - 0 \\ 0 - 0 = y - 1 \\ 0 - 0 = z - 0 \end{matrix} \Leftrightarrow \{\begin{matrix} x = 1 \\ y = 1 \\ z = 0 \end{matrix} \Rightarrow C (1; 1; 0)$

Lại có

$\begin{array}{l} M (\frac{1}{2}; 0; 0), N (\frac{1}{2}; 1; 0) \Rightarrow \vec{M N} = (0; 1; 0), \vec{A^{'} C} = (1; 1; - 1), \vec{M A^{'}} = (- \frac{1}{2}; 0; 1) \\ \Rightarrow [\vec{M N}, \vec{A^{'} C}] = (|\begin{matrix} \begin{array}{l} 1 \\ 1 \end{array} & \begin{array}{l} 0 \\ - 1 \end{array} \end{matrix}|; |\begin{matrix} \begin{array}{l} 0 \\ - 1 \end{array} & \begin{array}{l} 0 \\ 1 \end{array} \end{matrix}|; |\begin{matrix} \begin{array}{l} 0 \\ 1 \end{array} & \begin{array}{l} 1 \\ 1 \end{array} \end{matrix}|) = (- 1; 0; - 1) \end{array}$

Vậy

$d (M N, A^{'} C) = \frac{|[\vec{M N}, \vec{A^{'} C}] . \vec{M A^{'}}|}{|[\vec{M N}, \vec{A^{'} C}]|} = \frac{|(- 1) . (- \frac{1}{2}) + 0.0 + (- 1) .1|}{\sqrt{{(- 1)}^{2} + 0^{2} + {(- 1)}^{2}}} = \frac{1}{2 \sqrt{2}} = \frac{\sqrt{2}}{4}$

Đáp án cần chọn là: B

Câu 18:

Trong không gian Oxyz, đường thẳng $d : \frac{x + 2}{1} = \frac{y - 3}{2} = \frac{z - 11}{- 1}$ và hai điểm A(1;2;4), B(0;0;m) cùng nằm trong một mặt phẳng khi m bằng:

A. $\frac{15}{4}$

B. $\frac{15}{6}$

C. 5

D. 5

Bước 1: Xác định điểm M và VTCP của d.

Xét d có $M (- 2; 2; 11) \in d$ và $\vec{u} (1; 2; - 1)$ là vecto chỉ phương của d.

Ta có:

$\vec{A M} (- 3; 1; 7); \vec{A B} (- 1; - 2; m - 4)$

Bước 2:

Đường thẳng d, A, B đồng phẳng $\Leftrightarrow \vec{u}, \vec{A B}, \vec{A M}$ đồng phẳng.

$\Leftrightarrow [\vec{u}, \vec{A M}] . \vec{A B} = 0$

Bước 3:

Xét $[\vec{u}, \vec{A M}] . \vec{A B}$

$\begin{array}{l} = (|\begin{matrix} 2 & - 1 \\ 1 & 7 \end{matrix}|; |\begin{matrix} - 1 & 1 \\ 7 & - 3 \end{matrix}|; |\begin{matrix} 1 & 2 \\ - 3 & 1 \end{matrix}|) . \vec{A B} \\ = (15; - 4; 7) . (- 1; - 2; m - 4) \end{array}$

$= - 15 + 8 + 7 m - 28 = 7 m - 35$

$[\vec{u}, \vec{A M}] . \vec{A B} = 0 \Leftrightarrow 7 m - 35 = 0$ $\Leftrightarrow m = 5$

Đáp án cần chọn là: D

Câu 19:

Trong không gian Oxyz cho hai điểm M(−2;−2;1),A(1;2;−3) và đường thẳng $d : \frac{x + 1}{2} = \frac{y - 5}{2} = \frac{z}{- 1} .$ Gọi $Δ$ là đường thẳng qua M, vuông góc với đường thẳng d,d, đồng thời cách điểm A một khoảng bé nhất. Khoảng cách bé nhất đó là

A. $\sqrt{29}$

B. 6

C. 5

D. $\frac{\sqrt{34}}{9}$

Gọi (P) là mặt phẳng qua M(−2;−2;1) và nhận $\vec{u_{d}} = (2; 2; - 1)$ làm VTPT

Phương trình mặt phẳng $(P) : 2 (x + 2) + 2 (y + 2) - (z - 1) = 0$

$\Leftrightarrow 2 x + 2 y - z + 9 = 0$

Suy ra $Δ \subset (P)$ . Khi đó ta có $d (A, Δ) \geq d (A, (P))$

Lại có $d (A, (P)) = \frac{|2.1 + 2.2 - (- 3) + 9|}{\sqrt{2^{2} + 2^{2} + {(- 1)}^{2}}} = 6$

Vậy khoảng cách nhỏ nhất là d=6.

Đáp án cần chọn là: B

Câu 20:

Trong không gian Oxyz , cho đường thẳng $d : \frac{x - 3}{2} = \frac{y - 4}{1} = \frac{z - 2}{1}$ và 2 điểm A(6;3;−2); B(1;0;−1). Gọi $Δ$ là đường thẳng đi qua B, vuông góc với d và thỏa mãn khoảng cách từ A đến $Δ$ là nhỏ nhất. Một vectơ chỉ phương của $Δ$ có tọa độ :

A.(1;1;−3)

B.(1;−1;−1)

C.(1;2;−4)

D.(2;−1;−3)

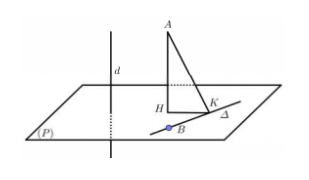
Media VietJack

Gọi (P) là mặt phẳng đi qua B và vuông góc với $d \Rightarrow (P) : 2 x + y + z - 1 = 0$

$Δ$ đi qua B và vuông góc với $d \Rightarrow Δ \subset (P)$

Gọi H,K lần lượt là hình chiếu của A lên (P) và $Δ$ ta có $A H \leq A K$

Do đó để khoảng cách từ A đến $Δ$ là nhỏ nhất $\Rightarrow H \in Δ$

Phương trình AH đi qua A và nhận $\vec{u_{d}} = (2; 1; 1)$ là 1 VTCP là $\{\begin{matrix} x = 6 + 2 t \\ y = 3 + t \\ z = - 2 + t \end{matrix}$

$\begin{array}{l} H \in A H \Rightarrow H (6 + 2 t; 3 + t; - 2 + t) \\ H \in (P) \Rightarrow 2 (6 + 2 t) + 3 + t - 2 + t - 1 = 0 \Leftrightarrow 6 t + 12 = 0 \Leftrightarrow t = - 2 \\ \Rightarrow H (2; 1; - 4) \end{array}$

$Δ$ đi qua B,H nhận $\vec{B H} (1; 1; - 3)$ là 1 VTCP.

Đáp án cần chọn là: A

Bắt đầu thi ngay

Có thể bạn quan tâm

Các bài thi hot trong chương