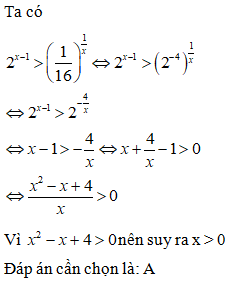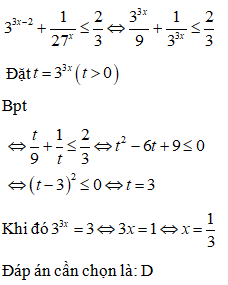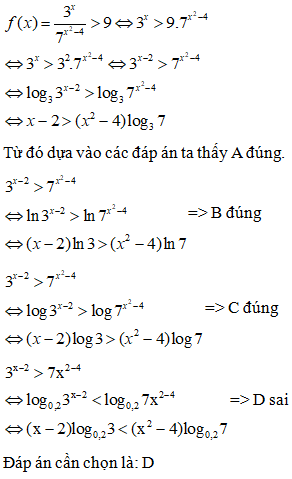19 câu hỏi trắc nghiệm thuộc Bất phương trình có mũ

Câu 1:

{(\frac{1}{2})}^{x} \geq 2

.

A. $(- \infty; - 1]$

B. $[- 1; + \infty)$

C. $(- \infty; - 1)$

D. $(- 1; + \infty)$

Xem đáp án

${(\frac{1}{2})}^{x} \geq 2 \Leftrightarrow 2^{- x} \geq 2 \Leftrightarrow - x \geq 1 \leftrightarrow x \leq - 1 \Rightarrow S = (- \infty; - 1]$

Đáp án cần chọn là: A

Câu 2:

Tìm tập nghiệm S của bất phương trình

2^{x - 1} > {(\frac{1}{16})}^{\frac{1}{x}}

A. $(0; + \infty)$

B. $(- \infty; + \infty)$

C. $(2; + \infty)$

D. $(- \infty; 0)$

Xem đáp án

Câu 3:

Tìm tập nghiệm của bất phương trình

{0,3}^{x^{2} + x} > 0,09

A. $(- \infty; - 2)$

B. $(- \infty; - 2) \cup (1; + \infty)$

C. (-2;1)

D. $(1; + \infty)$

Xem đáp án

${0,3}^{x^{2} + x} > 0,09 \Leftrightarrow {0,3}^{x^{2} + x} > {0,3}^{2} \Leftrightarrow x^{2} + x - 2 < 0 \Leftrightarrow - 2 < x < 1$

Đáp án cần chọn là: C

Câu 4:

Tìm tập nghiệm của bất phương trình

5^{x} < 7 - 2 x

A. R

B. $(- \infty; 1)$

C. $(1; + \infty)$

D. $\emptyset$

Xem đáp án

Câu 5:

Nghiệm của bất phương trình

e^{x} + e^{- x} < \frac{5}{2}

là

A. x < -ln2 hoặc x > ln2

B. -ln2 < x < ln2

C. $x < \frac{1}{2} hoặc x > 2$

D. $\frac{1}{2} < x < 2$

Xem đáp án

$e^{x} + e^{- x} < \frac{5}{2} \Leftrightarrow e^{2 x} + 1 < \frac{5}{2} e^{x} \Leftrightarrow 2 e^{2 x} - 5 e^{x} + 2 < 0 \Leftrightarrow (e^{x} - 2) (2 e^{x} - 1) < 0 \Leftrightarrow \frac{1}{2} < e^{x} < 2 \Leftrightarrow - \ln 2 < x < \ln 2$

Đáp án cần chọn là: B

Câu 6:

Tìm tập nghiệm của bất phương trình

7^{x} \geq 10 - 3 x

A. $[1; + \infty)$

B. $(- \infty; 1]$

C. $(- \infty; \frac{10}{3})$

D. $(\frac{10}{3}; + \infty)$

Xem đáp án

Câu 7:

Tập hợp nghiệm của bất phương trình: $3^{3 x - 2} + \frac{1}{27^{x}} \leq \frac{2}{3}$ là:

A. (2;3)

B. (1;2)

C. {3}

D. $\{\frac{1}{3}\}$

Xem đáp án

Câu 8:

Bất phương trình ${(2 - \sqrt{3})}^{x} > {(2 + \sqrt{3})}^{x + 2}$ có tập nghiệm là:

A. $(- 1; + \infty)$

B. $(- \infty; - 1)$

C. $(2; + \infty)$

D. $(- \infty; - 2)$

Xem đáp án

$\begin{array}{l} t = (2 - \sqrt{3}) (1 > t > 0) \Rightarrow (2 + \sqrt{3}) = \frac{1}{t} \\ \Rightarrow t^{x} > {(\frac{1}{t})}^{x + 2} \Rightarrow t^{x} > t^{- x - 2} \Rightarrow x < - x - 2 \Rightarrow x < - 1 \end{array}$

Đáp án cần chọn là: B

Câu 9:

Tìm số nghiệm nguyên của bất phương trình

{(\frac{1}{3})}^{\sqrt{x^{2} - 3 x - 10}} > {(\frac{1}{3})}^{x - 2}

A. Vô số

B. 0

C. 9

D. 11

Xem đáp án

Vì $0 < \frac{1}{3} < 1$ nên ta có

${(\frac{1}{3})}^{\sqrt{x^{2} - 3 x - 10}} > {(\frac{1}{3})}^{x - 2} \Leftrightarrow \sqrt{x^{2} - 3 x - 10} < x - 2 \Leftrightarrow \{\begin{matrix} x^{2} - 3 x - 10 < {(x - 2)}^{2} \\ x^{2} - 3 x - 10 \geq 0 \\ x - 2 > 0 \end{matrix} \Leftrightarrow 5 \leq x < 14 \Rightarrow x = {5,6,7,8,9,10,11,12,13}$

Đáp án cần chọn là: C

Câu 10:

Tìm số nghiệm nguyên của bất phương trình

{(\frac{1}{5})}^{x^{2} - 2 x} \geq \frac{1}{125}

A. Vô số

B. 6

C. 4

D. 5

Xem đáp án

Ta có

$\begin{array}{l} {(\frac{1}{5})}^{x^{2} - 2 x} \geq \frac{1}{125} \Leftrightarrow {(\frac{1}{5})}^{x^{2} - 2 x} \geq {(\frac{1}{5})}^{3} \\ \Leftrightarrow x^{2} - 2 x \leq 3 \Leftrightarrow x^{2} - 2 x - 3 \leq 0 \Leftrightarrow - 1 \leq x \leq 3 \end{array}$

Số nghiệm nguyên là 5.

Đáp án cần chọn là: D

Câu 11:

Tập nghiệm của bất phương trình

{(x^{2} + x + 1)}^{x} < 1

là:

A. $(0; + \infty)$

B. $(- \infty; 0)$

C. $(- \infty; - 1)$

D. (0;1)

Xem đáp án

${(x^{2} + x + 1)}^{x} < 1$

Lấy loganepe hai vế ta có $\ln {(x^{2} + x + 1)}^{x} < \ln 1 (*)$

Vì

$x^{2} + x + 1 = {(x + \frac{1}{2})}^{2} + 34 > 0 \Rightarrow (*) \Leftrightarrow x l n (x^{2} + x + 1) < 0 \Leftrightarrow [\begin{matrix} \{\begin{matrix} x < 0 \\ l n (x^{2} + x + 1) > 0 \end{matrix} \\ \{\begin{matrix} x > 0 \\ l n (x^{2} + x + 1) < 0 \end{matrix} \end{matrix} \Leftrightarrow [\begin{matrix} \{\begin{matrix} x < 0 \\ x^{2} + x + 1 > 1 \end{matrix} \\ \{\begin{matrix} x > 0 \\ x^{2} + x + 1 < 1 \end{matrix} \end{matrix} \Leftrightarrow [\begin{matrix} \{\begin{matrix} x < 0 \\ x^{2} + x > 0 \end{matrix} \\ \{\begin{matrix} x > 0 \\ x^{2} + x < 0 \end{matrix} \end{matrix} \Leftrightarrow [\begin{matrix} \{\begin{matrix} x < 0 \\ [\begin{matrix} x > 0 \\ x < - 1 \end{matrix} \end{matrix} \\ \{\begin{matrix} x > 0 \\ - 1 < x < 0 \end{matrix} \end{matrix} \Leftrightarrow x < - 1$

Vậy tập nghiệm của bất phương trình là $(- \infty; - 1)$

Đáp án cần chọn là: C

Câu 12:

Tập nghiệm của bất phương trình

3^{\sqrt{2 x} + 1} - 3^{x + 1} \leq x^{2} - 2 x

là:

A. $(0; + \infty)$

B. [0;2]

C. $[2; + \infty)$

D. $[2; + \infty) \cup \{0\}$

Xem đáp án

ĐK: $x \geq 0$

$3^{\sqrt{2 x} + 1} - 3^{x + 1} \leq x^{2} - 2 x \Leftrightarrow 3^{\sqrt{2 x} + 1} + 2 x \leq 3^{x + 1} + x^{2} \Leftrightarrow 3^{\sqrt{2 x} + 1} + {(\sqrt{2 x})}^{2} \leq 3^{x + 1} + x^{2}$

Xét hàm số $f (t) = 3^{t + 1} + t^{2}$ có $f^{'} (t) = 3^{t + 1} . \ln 3 + 2 t > 0 \forall t \geq 0 \Rightarrow$ Hàm số đồng biến trên $[0; + \infty)$

Mà $f (\sqrt{2 x}) \leq f (x) \Leftrightarrow \sqrt{2 x} \leq x \Leftrightarrow 2 x \leq x^{2} \Leftrightarrow x^{2} - 2 x \geq 0 \Leftrightarrow x \in (- \infty; 0] \cup [2; + \infty) Mà x \geq 0 \Rightarrow x \in [2; + \infty) \cup \{0\}$

Đáp án cần chọn là: D

Câu 13:

Số nghiệm nguyên của bất phương trình

4^{x} - {5.2}^{x} + 4 < 0

là:

A. 1

B. 2

C. 0

D. 3

Xem đáp án

Câu 14:

Có bao nhiêu giá trị thực của m để bất phương trình

4^{x} - (m + 1) 2^{x} + m < 0

vô nghiệm?

A. 2

B. vô số

C. 1

D. 0

Xem đáp án

Câu 15:

Cho hàm số

f (x) = \frac{3^{x}}{7^{x^{2} - 4}}

. Hỏi khẳng định nào sau đây là sai?

A. $f (x) > 9 \Leftrightarrow x - 2 - (x^{2} - 4) \log_{3} 7 > 0$

B. $f (x) > 9 \Leftrightarrow (x - 2) \ln 3 - (x^{2} - 4) \ln 7 > 0$

C. $f (x) > 9 \Leftrightarrow (x - 2) \log 3 - (x^{2} - 4) \log 7 > 0$

D. $f (x) > 9 \Leftrightarrow (x - 2) \log_{0,2} 3 - (x^{2} - 4) \log_{0,2} 7 > 0$

Xem đáp án

Câu 16:

Cho hàm số y = f(x). Hàm số y = f′(x) có bảng biến thiên như sau:

Bất phương trình $f (x) < e^{x} + m$ đúng với mọi $x \in (- 1; 1)$ khi và chỉ khi:

A. $m \geq f (1) - e$

B. $m > f (- 1) - \frac{1}{e}$

C. $m \geq f (- 1) - \frac{1}{e}$

D. $m > f (1) - e$

Xem đáp án

Câu 17:

Có bao nhiêu giá trị nguyên của tham số m để bất phương trình

(3^{x^{2} - x} - 9) (2^{x^{2}} - m) \leq 0

có 5 nghiệm nguyên?

A. 65021

B. 65024

C. 65022

D. 65023

Xem đáp án

Câu 18:

Gọi S là tập hợp các số tự nhiên n có 4 chữ số thỏa mãn

{(2^{n} + 3^{n})}^{2020} < {(2^{2020} + 3^{2020})}^{n}

. Số phần tử của S là:

A. 8999

B. 2019

C. 1010

D. 7979

Xem đáp án

$\begin{array}{l} {(2^{n} + 3^{n})}^{2020} < {(2^{2020} + 3^{2020})}^{n} \\ \Leftrightarrow \ln {(2^{n} + 3^{n})}^{2020} < \ln {(2^{2020} + 3^{2020})}^{n} \\ \Leftrightarrow 2020 \ln (2^{n} + 3^{n}) < n \ln (2^{2020} + 3^{2020}) \\ \Leftrightarrow \frac{\ln (2^{n} + 3^{n})}{n} < \frac{\ln (2^{2020} + 3^{2020})}{2020} \end{array}$

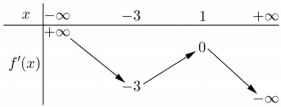
Xét hàm đặc trưng $f (x) = \frac{\ln (2^{x} + 3^{x})}{x} (x \in ℕ^{*})$ ta có:

$f' (x) = \frac{\frac{(2^{x} + 3^{x})'}{2^{x} + 3^{x}} . x - l n (2^{x} + 3^{x})}{x^{2}} \forall x \in ℕ^{*} f' (x) = \frac{(2^{x} l n 2 + 3^{x} l n 3) x - (2^{x} + 3^{x}) . l n (2^{x} + 3^{x})}{x^{2} (2^{x} + 3^{x})} \forall x \in ℕ^{*} = \frac{2^{x} l n 2. x - 2^{x} l n (2^{x} + 3^{x}) + 3^{x} l n 3. x - 3^{x} l n (2^{x} + 3^{x})}{x^{2} (2^{x} + 3^{x})} \forall x \in ℕ^{*} f' (x) = \frac{2^{x} (x l n 2 - l n (2^{x} + 3^{x})) + 3^{x} (x l n 3 - l n (2^{x} + 3^{x}))}{x^{2} (2^{x} + 3^{x})} \forall x \in ℕ^{*} f' (x) = \frac{2^{x} [l n 2^{x} - l n (2^{x} + 3^{x})] + 3^{x} [l n 3^{x} - l n (2^{x} + 3^{x})]}{x^{2} (2^{x} + 3^{x})} \forall x \in ℕ^{*}$

Vì $\{\begin{matrix} 2^{x} < 2^{x} + 3^{x} \Rightarrow l n 2^{x} < l n (2^{x} + 3^{x}) \\ 3^{x} < 2^{x} + 3^{x} \Rightarrow l n 3^{x} < l n (2^{x} + 3^{x}) \end{matrix} \Rightarrow f' (x) < 0 \forall x \in ℕ *$