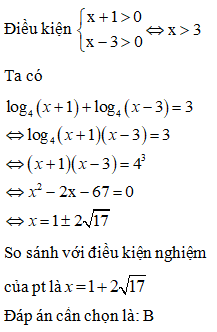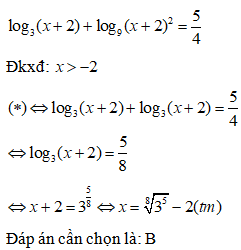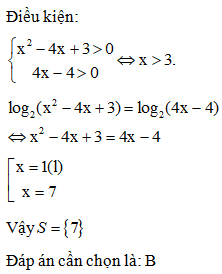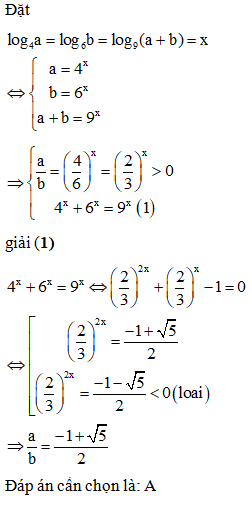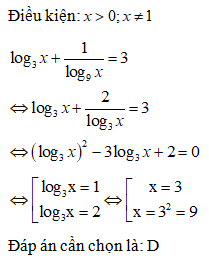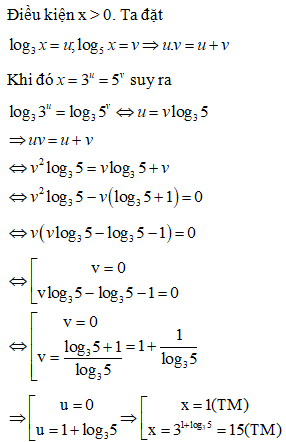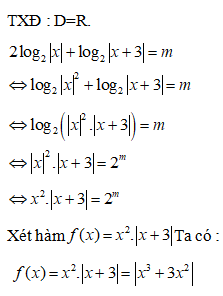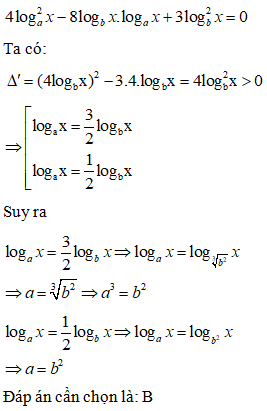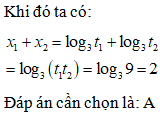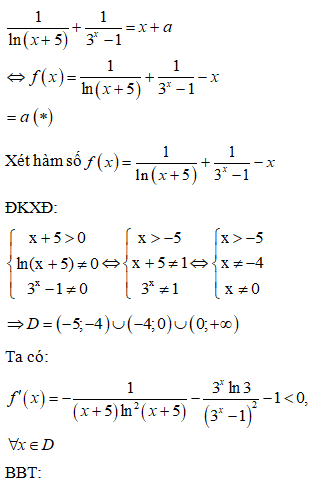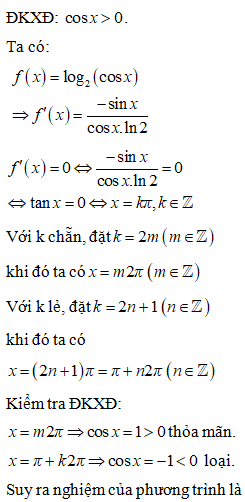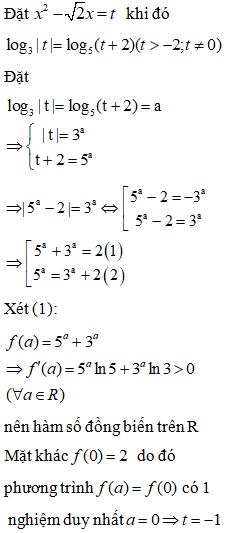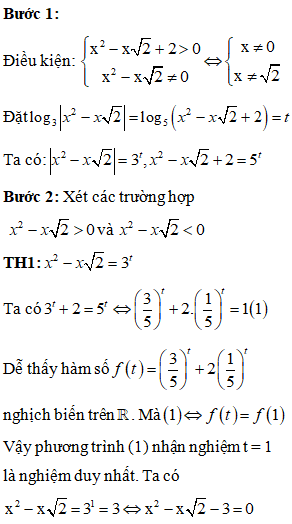Phương trình logarit
-
668 lượt thi
-
32 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 12:
Tập hợp nghiệm của phương trình là:
 Xem đáp án
Xem đáp án
Điều kiện:
Phương trình đã cho tương đương với:
Đáp án cần chọn là: B
Câu 13:
Giải phương trình Ta có nghiệm:
 Xem đáp án
Xem đáp án
Phương trình đã cho tương đương với:
Đáp án cần chọn là: C
Câu 19:
Phương trình sau đây có bao nhiêu nghiệm
 Xem đáp án
Xem đáp án
Đkxđ: x>0
Phương trình (*) có 3 nghiệm.
Đáp án cần chọn là: C
Câu 29:
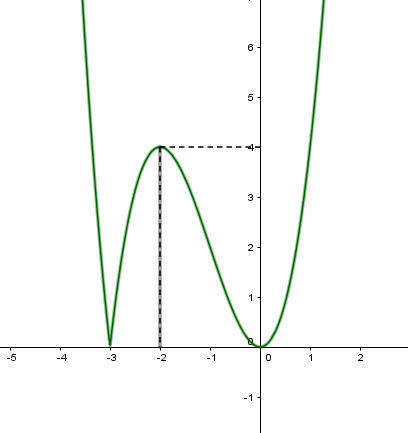
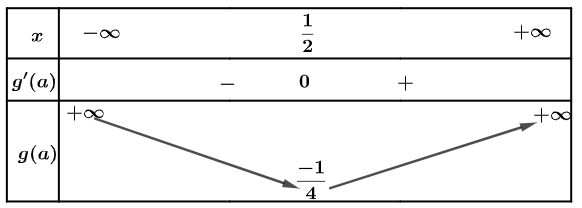
Tìm m để phương trình có nghiệm
 Xem đáp án
Xem đáp án
+ Cô lập với 1>x>0 .
+ Nhận xét đáp án: ta thấy Loại C và D
+ Tính giới hạn của khi x tiến dần tới 1 thì thấy y dần tiến tới 0 . Loại B.
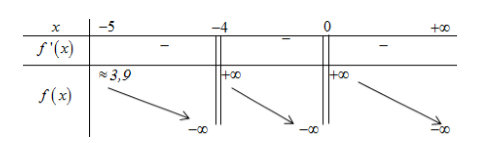
Đáp án cần chọn là: A