6 câu hỏi trắc nghiệm thuộc Ứng dụng thể tích các khối đa diện vào thực tế

Câu 1:

Ông A dự định sử dụng hết 5m² kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?

Xem đáp án

Bước 1: Gọi chiều rộng bể cá là x, tính chiều dài và chiều cao của bế cá theo x.

Gọi chiều rộng của bể cá là x (m) $(x > 0) \Rightarrow$ Chiều dài của bể cá là 2x(m)2x(m)

Gọi h là chiều cao của bể cá ta có

$2 x^{2} + 2 x h + 4 x h = 5 \Leftrightarrow 2 x^{2} + 6 x h = 5 \Leftrightarrow h = \frac{5 - 2 x^{2}}{6 x}$

Bước 2: Tính thể tích của bể cá theo x, sử dụng phương pháp hàm số tìm GTLN của thể tích bể cá.

Khi đó thể tích của bể cá là $2 x^{2} . \frac{5 - 2 x^{2}}{6 x} = \frac{1}{3} (5 x - 2 x^{3}) = \frac{1}{3} f (x)$

Xét hàm số $f (x) = 5 x - 2 x^{3} (x > 0)$ có $f^{'} (x) = 5 - 6 x^{2} = 0 \Leftrightarrow x = \sqrt{\frac{5}{6}}$ .

Lập BBT:

$\Rightarrow \max_{(0; + \infty)} f (x) = f (\sqrt{\frac{5}{6}})$

$\Rightarrow V_{\max} = \frac{1}{3} f (\sqrt{\frac{5}{6}}) = \frac{5 \sqrt{50}}{27} \approx 1, 01 m^{3}$

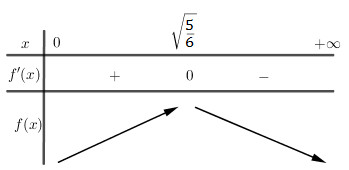
Câu 2:

Cho hình hộp ABCD⋅A′B′C′D′ có đáy ABCD là hình thoi cạnh a, $\hat{B C D} = 120^{\circ} .$ Biết rằng hình chiếu vuông góc của A′ lên mặt phẳng (ABCD) trùng với giao điểm của AC và BD. Diện tích tam giác A′AB bằng $\frac{a^{2} \sqrt{3}}{4}$

Tính góc giữa hai mặt phẳng (ABB′A′) và (ABC)

A. $30^{0}$

B. $45^{0}$

C. $60^{0}$

D. $90^{0}$

Xem đáp án

Bước 1: Tính diện tích tam giác ABH

Hình thoi ABCD có $\hat{B C D} = 120^{\circ}$

$\Rightarrow \hat{A B C} = 60^{\circ}$

Do đó ABC là tam giác đều

$\Rightarrow S_{A B C} = \frac{a^{2} \sqrt{3}}{4}$

$\Rightarrow S_{A B H} = \frac{1}{2} S_{A B C} = \frac{a^{2} \sqrt{3}}{8} .$

Bước 2: Sử dụng công thức liên hệ giữa diện tích hình chiếu của đa giác và đa giác ban đầu.

Tam giác ABH là hình chiếu của tam giác A′BH

Gọi góc giữa (ABB′A′) và (ABCD) là

Khi đó ta có $S_{A B H} = S_{A B A^{'}} \cos φ \Rightarrow \cos φ = \frac{S_{A B H}}{S_{A B A^{'}}} = \frac{1}{2} \Rightarrow φ = 60^{\circ}$

Đáp án cần chọn là: C

Câu 3:

Cho hình hộp ABCD⋅A′B′C′D′ có đáy ABCD là hình thoi cạnh a, $\hat{B C D} = 120^{\circ} .$ Biết rằng hình chiếu vuông góc của A′ lên mặt phẳng (ABCD) trùng với giao điểm của AC và BD. Diện tích tam giác A′AB bằng $\frac{a^{2} \sqrt{3}}{4}$

Tính thể tích khối lăng trụ ABCD⋅A′B′C′D′

A. $\frac{a^{3} \sqrt{3}}{8} .$

B. $\frac{3 a^{3} \sqrt{3}}{8} .$

C. $\frac{3 a^{3} \sqrt{3}}{5} .$

D. $\frac{6 a^{3} \sqrt{3}}{8} .$

Xem đáp án

Bước 1: Gọi M là trung điểm AB,I là trung điểm AM. Tính góc A’IH

Ta có $S_{A B C D} = 2 S_{A B C} = \frac{a^{2} \sqrt{3}}{2}$

Gọi M là trung điểm AB,I là trung điểm AM

Khi đó $H I ⊥ A B \Rightarrow$ góc giữa (ABB′A′) và (ABCD) là góc $\hat{A^{'} I H} = 60^{\circ}$

Bước 2: Tính $V_{A B C D \cdot A^{'} B^{'} C^{'} D^{'}}$

Ta có

$I H = \frac{1}{2} C M = \frac{a \sqrt{3}}{4} \Rightarrow A^{'} H = I H \cdot \tan 60^{\circ} = \frac{3 a}{4}$

$\Rightarrow V_{A B C D \cdot A^{'} B^{'} C^{'} D^{'}} = A^{'} H \cdot S_{A B C D} = \frac{3 a}{4} \cdot \frac{a^{2} \sqrt{3}}{2} = \frac{3 a^{3} \sqrt{3}}{8} .$

Đáp án cần chọn là: B

Câu 4:

Người ta cần chế tạo các món quà lưu niệm bằng đồng có dạng khối chóp tứ giác đều, được mạ vàng bốn mặt bên và có thể tích bằng $16 c m^{3}$ . Diện tích mạ vàng nhỏ nhất của khối chóp bằng bao nhiêu $c m^{2}$ ? (Kết quả làm tròn đến hàng đơn vị.)

Xem đáp án

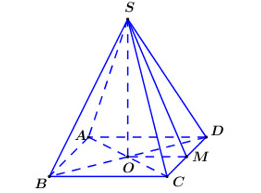
Bước 1: Giả sử chóp tứ giác đều là $S . A B C D$ . Gọi $O = A C \cap B D$ đặt $A B = x (x > 0)$ tính SO theo x.

Giả sử chóp tứ giác đều là S.ABCD. Gọi $O = A C \cap B D \Rightarrow S O ⊥ (A B C D)$

Đặt $A B = x (x > 0)$ ta có $S_{A B C D} = x^{2}$

\Rightarrow V_{S . A B C D} = \frac{1}{3} S O . S_{A B C D} = \frac{1}{3} S O . x^{2} = 16 \Leftrightarrow S O = \frac{48}{x^{2}}

Bước 2: Gọi M là trung điểm của CD. Tính SM theo x, từ đó tính $S_{Δ S C D}$ theo x.

Gọi M là trung điểm của CD ta có $\{\begin{matrix} C D ⊥ O M \\ C D ⊥ S O \end{matrix} \Rightarrow C D ⊥ (S O M) \Rightarrow C D ⊥ S M$

Ta có $O M = \frac{1}{2} A D = \frac{1}{2} A B = \frac{x}{2}$ áp dụng định lí Pytago ta có:

S M = \sqrt{S O^{2} + O M^{2}} = \sqrt{{(\frac{48}{x^{2}})}^{2} + \frac{x^{2}}{4}}

\Rightarrow S_{Δ S C D} = \frac{1}{2} S M . C D = \frac{1}{2} \sqrt{{(\frac{48}{x^{2}})}^{2} + \frac{x^{2}}{4}} . x = \frac{1}{2} \sqrt{\frac{48^{2}}{x^{2}} + \frac{x^{4}}{4}}

Bước 3: Tìm GTNN của diện tích mạ vàng

Để diện tích mạ vàng nhỏ nhất thì $S_{Δ S C D}$ nhỏ nhất $\Rightarrow \frac{48^{2}}{x^{2}} + \frac{x^{4}}{4}$ đạt giá trị nhỏ nhất.

Ta có $\frac{48^{2}}{x^{2}} + \frac{x^{4}}{4} = \frac{1152}{x^{2}} + \frac{1152}{x^{2}} + \frac{x^{4}}{4} \geq 3 \sqrt[3]{\frac{1152}{x^{2}} . \frac{1152}{x^{2}} . \frac{x^{4}}{4}} \geq 3. \sqrt[3]{331776}$ (BĐT Cô-si).

Vậy diện tích mạ vàng nhỏ nhất là $4.3. \sqrt[3]{331776} \approx 831 c m^{3}$

Câu 5:

Khi xây nhà, cô Ngọc cần xây một bể đựng nước mưa có thể tích $V = 6 m^{3}$ dạng hình hộp chữ nhật với chiều dài gấp ba lần chiều rộng, đáy và nắp và các mặt xung quanh đều được đổ bê tông cốt thép. Phần nắp bể để hở một khoảng hình vuông có diện tích bằng $\frac{2}{9}$ diện tích nắp bể. Biết rằng chi phí cho $1 m^{2}$ bê tông cốt thép là 1.000.000d. Tính chi phí thấp nhất mà cô Ngọc phải trả khi xây bể (làm tròn đến hàng trăm nghìn và các chữ số viết liền)?

Xem đáp án

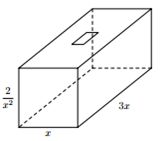
Bước 1: Gọi x(m),3x(m) lần lượt là chiều rộng, chiều dài của bể. Tính chiều cao của bể.

Gọi x(m),3x(m) lần lượt là chiều rộng, chiều dài của bể, h là chiều cao của bể.

Theo bài ra ta có: $V = x .3 x . h = 6 \Rightarrow h = \frac{6}{3 x^{2}} = \frac{2}{x^{2}} (m)$

Bước 2: Tính tổng diện tích các mặt làm bê tông.

Khi đó tổng diện tích các mặt bể được làm bê tông là:

2 x . \frac{2}{x^{2}} + 2.3 x . \frac{2}{x^{2}} + 2 x .3 x - x .3 x . \frac{2}{9} = \frac{16 x^{2}}{3} + \frac{16}{x}

Bước 3: Sử dụng BĐT Cô-si cho 3 số dương để tính số tiền ít nhất cần tìm

Áp dụng BĐT Cô-si ta có:

\frac{16 x^{2}}{3} + \frac{16}{x} = \frac{16 x^{2}}{3} + \frac{8}{x} + \frac{8}{x} \geq 3 \sqrt[3]{\frac{16 x^{2}}{3} . \frac{8}{x} . \frac{8}{x}} = 8 \sqrt[3]{18}

Dấu “=” xảy ra khi $\frac{16 x^{2}}{3} = \frac{8}{x} \Leftrightarrow x = \sqrt[3]{\frac{3}{2}}$

Vậy số tiền ít nhất mà cô Ngọc cần bỏ ra là $8 \sqrt[3]{18} {.10}^{6} \approx 21.000.000 d$

Câu 6:

Cho một cây nến hình lăng trụ lục giác đều có chiều cao và độ dài cạnh đáy lần lượt là 15cm và 5cm. Người ta xếp cây nến trên vào trong một hộp có dạng hình hộp chữ nhật sao cho cây nến nằm khít trong hộp ( có đáy tiếp xúc như hình vẽ). Thể tích của chiếc hộp đó bằng.

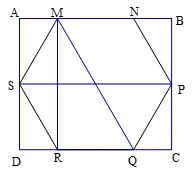
Media VietJack