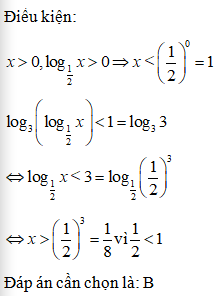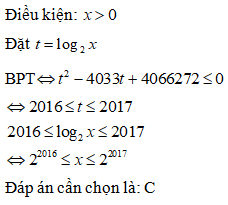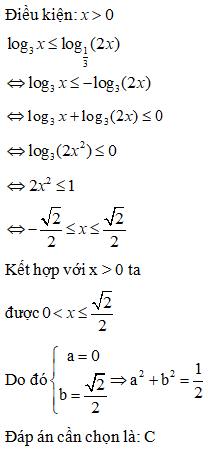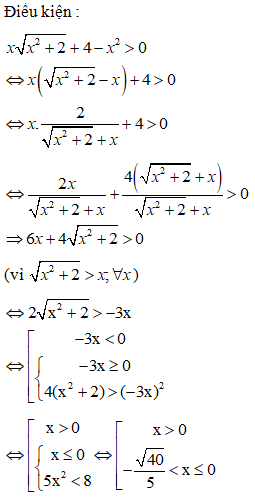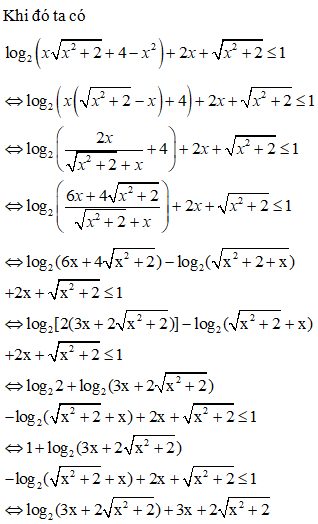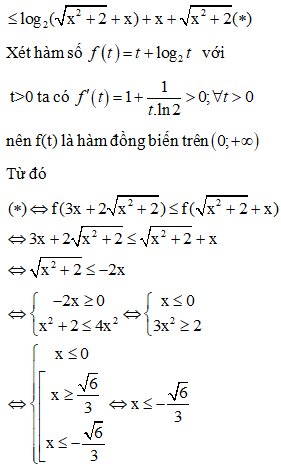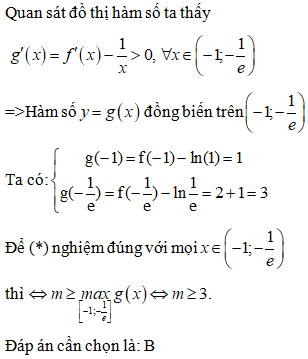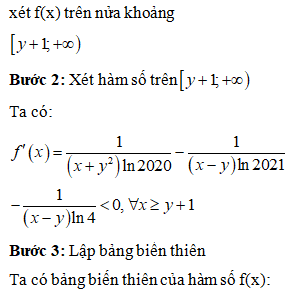Bất phương trình có logarit
-
499 lượt thi
-
27 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 2:
 Xem đáp án
Xem đáp án
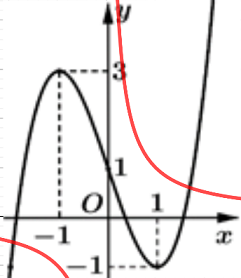
Điều kiện:
BPT
Kết hợp điều kiện ta được
Đáp án cần chọn là: A
Câu 3:
 Xem đáp án
Xem đáp án
Điều kiện:
Kết hợp với điều kiện suy ra S = (1;2)
Đáp án cần chọn là: DCâu 5:
 Xem đáp án
Xem đáp án
Điều kiện: x>-2
Bất phương trình
Nên x > 3 hoặc x < −1.
Kết hợp điều kiện x > −2 ta được x > 3 hoặc -2<x<-1.
Đáp án cần chọn là: C
Câu 7:
 Xem đáp án
Xem đáp án
Điều kiện:
Vậy số nguyên nhỏ nhất thỏa mãn bất phương trình là x = 8.
Đáp án cần chọn là: B
Câu 9:
 Xem đáp án
Xem đáp án
Điều kiện: x > 0
Tập nghiệm của bất phương trình là:
Đáp án cần chọn là: BCâu 11:
 Xem đáp án
Xem đáp án
Đkxđ:
Xét dấu
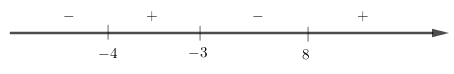
Vậy -4 < x < -3 hoặc x > 8
Kết hợp với điều kiện ta được -4 < x < -3 hoặc x > 8.
Đáp án cần chọn là A
Câu 12:
 Xem đáp án
Xem đáp án
Điều kiện: x > 1
Đáp án cần chọn là: A
Câu 18:
 Xem đáp án
Xem đáp án
Điều kiện:
Do x = 1 là một nghiệm của bất phương trình nên
Khi đó, ta có:
Kết hợp với điều kiện xác định ta có nghiệm của bpt là:
Đáp án cần chọn là: C
Câu 19:
 Xem đáp án
Xem đáp án
Thử giá trị Loại đáp án A
Thử giá trị Loại đáp án D
Thử giá trị x = 0,5: MATH ERROR: Loại đáp án C
Đáp án cần chọn là: B
Câu 21:
 Xem đáp án
Xem đáp án
ĐKXĐ: x > 0.
Ta có:
Lấy logarit cơ số 9 cả 2 vế bất phương trình ta được:
Kết hợp điều kiện xác định ta có
Vậy tập nghiệm của bất phương trình là:
Đáp án cần chọn là: B