50 câu hỏi trắc nghiệm thuộc Tổng hợp đề thi thptqg môn Toán cực hay mới nhất - đề 5

Câu 1:

Cho lăng trụ đứng ABC.A′B′C′ có đáy là tam giác cân, $AB = AC = 2 a, \hat{BAC} = 120 °$ . Mặt phẳng $(AB' C')$ tạo với đáy một góc $60 °$ . Thể tích khối lăng trụ bằng

A. $\frac{a^{3}}{2}$ (dvtt)

B. $a^{3}$ (dvtt)

C. $\frac{a^{3}}{6}$ (dvtt)

D. $3 a^{3}$ (dvtt)

Xem đáp án

Câu 2:

Hoành độ giao điểm của đồ thị hàm số $y = x^{4} - 3 x^{2} - 4$ và trục hoành là

A. −1; 1

B. −2; 2

C. −2; −1; 1; 2

D. −2; −1; 2

Xem đáp án

Câu 3:

Cho hình chóp $S . ABCD$ có đáy $ABCD$ là hình vuông cạnh 2a, $SD = \frac{a \sqrt{23}}{2}$ . Hình chiếu vuông góc của $S$ lên mặt phẳng $(ABCD)$ là trung điểm H của đoạn AB . Thể tích của chóp $S . ABCD$ là

A. $\frac{2 \sqrt{3} a^{3}}{3}$

B. $\frac{\sqrt{3} a^{3}}{6}$

C. $\frac{\sqrt{3} a^{3}}{2}$

D. $2 \sqrt{3} a^{3}$

Xem đáp án

Câu 4:

Cho đường thẳng $(d) : \frac{x - 2}{2} = \frac{y - 2}{1} = \frac{z}{2}$ và điểm $A (2; 3; 1)$ . Phương trình mặt phẳng $(P)$ chứa A và $(d)$ là

A. $x + y + z - 6$

B. $- x - 2 y + 2 z + 6 = 0$

C. $2 x - 3 y + 5 = 0$

D. $x + 2 y + z - 9 = 0$

Xem đáp án

Câu 5:

Phát biểu nào sau đây là đúng?

A. Hai số phức bằng nhau khi và chỉ khi phần thực của hai số đó bằng nhau và phần ảo của hai số đó bằng nhau

B. Hai số phức bằng nhau khi và chỉ khi hai phần thực của hai số đó bằng nhau

C. Hai số phức bằng nhau khi và chỉ khi môđun của hai số đó bằng nhau

D. Hai số phức bằng nhau khi và chỉ khi hai phần ảo của hai số đó bằng nhau

Xem đáp án

Đáp án A

Hai số phức bằng nhau khi và chỉ khi phần thực của hai số đó bằng nhau và phần ảo của hai số đó bằng nhau.

Câu 6:

Phương trình tiếp tuyến của đồ thị hàm số $y = f (x) = x^{4}$ tại điểm có hoành độ bằng -1 là

A. $y = - 4 x + 5$

B. $y = - 4 x - 4$

C. $y = - 4 x - 3$

D. $y = - 4 x - 5$

Xem đáp án

Câu 7:

Tìm m để phương trình $4^{x} - 2^{x + 2} + 3 = m$ có hai nghiệm thực.

A. $- 1 < m < 3$

B. $m > - 1$

C. $m < 3$

D. $m \geq 1$

Xem đáp án

Câu 8:

Tìm số phù hợp tiếp theo của dãy số sau đây: 1, 11, 21, 1211, 111221,…

A. 312211

B. 32121

C. 132111

D. 23421

Xem đáp án

Đáp án A

Có thể gọi đây là dãy số “nhìn và đọc”, cứ số đằng sau thì mô tả số ngay trước nó. Ví dụ:

1 (tức là có một số 1) thì số sau đó là 11

11 (tức là có hai số 1) thì số sau đó là 21

21 (tức là có một số 2 và một số 1) thì số sau đó là: 1211

…

Tiếp tục như vậy, 11221 (tức là có ba số 1, hai số 2 và một số 1) thì số tiếp sau đó là 312211.

Câu 9:

Tính đạo hàm của hàm số $y = \frac{sinx}{e^{x}}$

A. $\frac{cosx + sinx}{e^{2^{x}}}$

B. $\frac{cosx - sinx}{e^{x}}$

C. $\frac{cosx - sinx}{e^{2^{x}}}$

D. $\frac{cosx . e^{x} + sinx . e^{x}}{e^{2^{x}}}$

Xem đáp án

Câu 10:

Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số $y = 3 sinx - 4 cosx + 1 .$ Khẳng định nào sau đây là đúng?

A. $M = 4; m = - 6$

B. $M = 6; m = - 4$

C. $M = 5; m = - 5$

D. $M = 3; m = - 4$

Xem đáp án

Câu 11:

Cho hàm số $f (x) = \{\begin{cases} \sqrt{6 - 2 x} + 1 vs x \leq 3 \\ ax v s x > 3 \end{cases}$ . Với giá trị thực nào của a thì hàm số liên tục tại $x = 3$ ?

A. $x = - \frac{1}{3}$

B. x=3

C. $x = \frac{1}{3}$

D. x=-2

Xem đáp án

Câu 12:

Nếu phép tịnh tiến biến điểm $A (1; 2)$ thành điểm $A' (- 2; 3)$ thì nó biến điểm $B (0; 1)$ thành điểm nào?

A. $(- 3; 2)$

B. $(3; 0)$

C. $(3; - 2)$

D. $(- 3; 1)$

Xem đáp án

Câu 13:

Nguyên hàm của hàm số $y = 50 x . e^{\frac{- x}{2}}$ trên tập các số thực là

A. $- 100 x . e^{\frac{- x}{2}} + 50 e^{\frac{- x}{2}} + C$

B. $- 100 x . e^{\frac{- x}{2}} - 50 e^{\frac{- x}{2}} + C$

C. $- 100 x . e^{\frac{- x}{2}} + 200 e^{\frac{- x}{2}} + C$

D. $- 100 x . e^{\frac{- x}{2}} - 200 e^{\frac{- x}{2}} + C$

Xem đáp án

Câu 14:

Chu vi của một đa giác là 158cm, số đo các cạnh của nó lập thành một cấp số cộng với công sai $d = 3$ cm. Biết cạnh lớn nhất là 44cm. Số các cạnh của đa giác đó là

A. 5

B. 3

C. 4

D. 6

Xem đáp án

Câu 15:

Cho hàm số $f (x) = \frac{x^{2} - 4 x}{7 x}$ với $x \neq 0$ . Phải bổ sung thêm giá trị $f (0)$ bằng bao nhiêu thì hàm số liên tục trên R?

A. $\frac{1}{7}$

B. $\frac{- 4}{7}$

C. $\frac{4}{7}$

D. 0

Xem đáp án

Câu 16:

Tính giá trị nhỏ nhất của hàm số $y = \log_{2}^{2} x - 4 \log_{2} x + 1$ trên đoạn [1;8].

A. $- 2$

B. $- 1$

C. $- 4$

D. $- 3$

Xem đáp án

Câu 17:

Đồ thị hàm số $y = 2 x^{3} - 6 x + 1$ có mấy điểm cực trị?

A. 2

B. 1

C. Đáp án khác

D. 0

Xem đáp án

Câu 18:

Cho hàm số $y = f (x)$ có đạo hàm là $f' (x) = \frac{1}{2 x - 1}$ và $f (1) = 1$ thì $f (5)$ có giá trị là

A. ln 5+1

B. ln 2

C. ln 5

D. ln 3+1

Xem đáp án

Câu 19:

Trong không gian với hệ tọa độ Oxyz, cho ba điểm $A (- 3; 4; 2)$ , $B (- 5; 6; 2)$ , $C (- 4; 7; - 1)$ . Tìm tọa độ điểm D thỏa mãn $\vec{AD} = 2 \vec{AB} + 3 \vec{AC} .$

A. $(10; - 17; - 7)$

B. $(- 10; - 17; - 7)$

C. $(10; 17; 7)$

D. $(- 10; 17; - 7)$

Xem đáp án

Câu 20:

Phương trình $9^{x} - 4 {.3}^{x} + 3 = 0$ có hai nghiệm $x_{1}, x_{2} (x_{1} < x_{2})$ .Tính giá trị của biểu thức $A = 2 {x_{1}}^{2} + {x_{2}}^{2}$

A. 4

B. 3

C. 1

D. 2

Xem đáp án

Câu 21:

Trong tủ giày có 6 đôi giày. Lấy ngẫu nhiên 4 chiếc giày. Tìm xác suất sao cho trong các chiếc giày lấy ra có đúng 1 đôi giày

A. $\frac{16}{33}$

B. $\frac{4}{33}$

C. $\frac{6}{11}$

D. $\frac{26}{55}$

Xem đáp án

Câu 22:

Điều kiện xác định của hàm số $y = \frac{1}{\cot 2 x}$ là

A. $x \neq \frac{kπ}{2}, k \in Z$

B. $x \neq kπ, k \in Z$

C. $x \neq \frac{π}{2} + \frac{kπ}{2}, k \in Z$

D. $x \neq \frac{kπ}{4}, k \in Z$

Xem đáp án

Câu 23:

Cho hàm số $y = \frac{3 x + 2}{x - 3}$ .Chọn khẳng định đúng trong các khẳng định sau?

A. Hàm số đã cho luôn nghịch biến trên các nửa khoảng (−∞; 3] và [3; +∞)

B. Hàm số đã cho đồng biến trên R

C. Hàm số đã cho luôn nghịch biến trên các khoảng (−∞; 3) và (3; +∞)

D. Hàm số đã cho luôn đồng biến trên các khoảng (−∞; 3) và (3; +∞)

Xem đáp án

Câu 24:

Cho hình hộp chữ nhật $ABCD . A ’ B ’ C ’ D ’$ có $AB = AA ’ = a, AD = a \sqrt{3}$ . Khoảng cách giữa BD và CD' bằng

A. $a \sqrt{\frac{3}{5}}$

B. 2a

C. $a \sqrt{7}$

D. $a \sqrt{\frac{7}{3}}$

Xem đáp án

Đáp án D

Kẻ CM vuông góc với B’D’; MJ vuông góc với BD; JK vuông góc với CM. Chứng minh khoảng cách giữa BD và CD’ bằng độ dài đoạn JK.

Thật vậy, ta có

Câu 25:

Cho hình chóp tam giác đều $S . ABC$ có cạnh đáy bằng 2a, góc giữa cạnh bên và mặt đáy bằng $60^{o}$ . Khoảng cách từ điểm S đến mặt đáy $(ABC)$ là

A. 2a

B. $\sqrt{2} a$

C. $\sqrt{3} a$

D. a

Xem đáp án

Câu 26:

Cho số phức $z + (1 - i) \bar{z} = 4 + i$ . Môđun của số phức z là

A. 5

B. $\sqrt{37}$

C. 4

D. 2

Xem đáp án

Câu 27:

Có 2 chiếc hộp, mỗi hộp chứa 5 chiếc thẻ đều được đánh số từ 1 đến 5. Từ mỗi hộp rút ngẫu nhiên ra 1 chiếc thẻ. Tính xác suất để rút được 2 thẻ có tổng số ghi trên hai tấm thẻ bằng 6?

A. $\frac{2}{25}$

B. $\frac{1}{5}$

C. $\frac{3}{25}$

D. $\frac{4}{25}$

Xem đáp án

Câu 28:

Số điểm biểu diễn nghiệm của phương trình $\sin 2 x + 4 (cosx - sinx) = 4$ trên đường tròn lượng giác là

A. 2

B. 1

C. 4

D. 3

Xem đáp án

Câu 29:

Cho tam giác ABC với trọng tâm G, trực tâm H và tâm đường tròn ngoại tiếp O. Phép vị tự $V_{(O; k)}$ biến O thành H. Tìm k.

A. $- \frac{1}{2}$

B. 2

C. $\frac{1}{2}$

D. -2

Xem đáp án

Câu 30:

Điểm biểu diễn số phức liên hợp của số phức $z = - 1 - 2 i$ là

A. $(- 1; - 2 i)$ $(1; 2)$

B. $(- 1; 2)$

C. $(- 1; - 2)$

D. $(- 1; 2)$

Xem đáp án

Câu 31:

Đồ thị hàm số $y = \frac{x^{2} - 3 x + 4}{x - 2}$ có tiệm cận đứng là đường thẳng

A. $x = 2$

B. $y = 2$

C. $x = - 2$

D. $x = - 1$

Xem đáp án

Câu 32:

Hình vẽ sau đây giống với đồ thị của hàm số nào nhất?

A. $x^{3} + 3 x^{2} + 2$

B. $- x^{3} - 3 x + 2$

C. $x^{3} + 3 x - 4$

D. $x^{3} - 3 x + 2$

Xem đáp án

Câu 33:

Cho $I =_{0}^{\frac{π}{a}} \frac{\sin 2 x}{1 + \sin^{2} x} dx$ , với giá trị nguyên nào của $a$ thì $I =_{0}^{\frac{π}{a}} \frac{\sin 2 x}{1 + \sin^{2} x} dx = \ln 2 ?$

A. $a = - 2$

B. $a = 2$

C. $a = \pm 1$

D. $a = \pm 2$

Xem đáp án

Câu 34:

Trong không gian với hệ tọa độ $Oxyz$ , cho đường thẳng $d : \{\begin{cases} x = 2 + t \\ y = 1 - t \\ z = 3 + 2 t \end{cases}$ . Phương trình nào sau đây là phương trình chính tắc của d?

A. $d : \frac{x - 2}{1} = \frac{y + 1}{- 1} = \frac{z - 3}{2}$

B. $d : \frac{x + 2}{1} = \frac{y - 1}{- 1} = \frac{z + 3}{2}$

C. $d : \frac{x - 2}{1} = \frac{y - 1}{1} = \frac{z - 3}{2}$

D. $d : \frac{x - 2}{1} = \frac{y - 1}{- 1} = \frac{z - 3}{2}$

Xem đáp án

Câu 35:

Cho $P (A) = \frac{1}{4}; P (A \cup B) = \frac{1}{2}$ . Biết A và B là hai biến cố độc lập thì $P (B)$ bằng

A. $\frac{1}{4}$

B. $\frac{1}{3}$

C. $\frac{1}{2}$

D. $\frac{2}{3}$

Xem đáp án

Câu 36:

Cho đường tròn (C) có phương trình: ${(x - 1)}^{2} + {(y + 1)}^{2} = 4$ . Viết phương trình đường tròn (C’) là ảnh của (C) qua phép đối xứng qua trục Oy.

A. ${(x + 1)}^{2} + {(y + 1)}^{2} = 4$

B. ${(x - 1)}^{2} + {(y + 1)}^{2} = 4$

C. ${(x + 1)}^{2} + {(y - 1)}^{2} = 4$

D. ${(x - 1)}^{2} + {(y - 1)}^{2} = 4$

Xem đáp án

Đáp án A

Đường tròn (C) có tâm $I (1; - 1)$ và bán kính $R = 2$ . Qua phép đối xứng qua trục Oy tâm $I (1; - 1)$ biến thành $I ’ (- 1; - 1)$ và bán kính $R = 2$ không đổi.

Vậy đường tròn (C’) là ${(x + 1)}^{2} + {(y + 1)}^{2} = 4$

Câu 37:

Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = 4 x - x^{2}$ và $y = x^{3} - 4$ .

A. $\frac{71}{3}$

B. $\frac{71}{6}$

C. $\frac{57}{12}$

D. $\frac{27}{8}$

Xem đáp án

Câu 38:

Với giá trị nào của tham số m thì hàm số $y = x^{3} + 3 (m + 1) x^{2} + 1 - m$ đạt cực tiểu tại $x = - 1$ .

A. $m = \frac{1}{2}$

B. $m = - \frac{1}{2}$

C. $m = - \frac{3}{2}$

D. Không có giá trị nào của m thỏa mãn điều kiện đề bài

Xem đáp án

Câu 39:

Đến mùa sinh sản, một con cá hồi bơi ngược dòng để vượt một quãng đường 240km. Vận tốc dòng nước là 3km/h. Nếu vận tốc bơi của cá khi nước yên lặng là v(km/h) thì năng lượng tiêu hao của con cá trong t giờ được cho bởi công thức $E (v) = {cv}^{3} t$ , trong đó c là hằng số, E được tính bằng jun. Tìm vận tốc của con cá khi nước đứng yên để năng lượng tiêu hao là ít nhất.

A. $\frac{9}{2} km$

B. $5 km$

C. $9 km$

D. $6 km$

Xem đáp án

Câu 40:

Nếu $\log_{12} 6 = a$ và $\log_{12} 7 = b$ thì

A. $\log_{2} 7 = \frac{b}{1 + a}$

B. $\log_{2} 7 = \frac{1 - a}{b}$

C. $\log_{2} 7 = \frac{1 - a}{b}$

D. ${log}_{2} 7 = \frac{1 + a}{b}$

Xem đáp án

Câu 41:

Với giá trị nào của m thì hàm số $y = \frac{sinx - m}{sinx + m}$ đồng biến trên khoảng $(0; \frac{π}{2})$

A. $- 1 < m$

B. $- 1 < m < 0$

C. $m \leq - 1$

D. $- 1 \leq m \leq 0$

Xem đáp án

Câu 42:

Cho $a, b$ là hai số dương. Gọi K là hình phẳng nằm trong góc phần tư thứ hai, giới hạn bởi parabol $y = {ax}^{2}$ và đường thẳng $y = - b x$ . Thể tích khối tròn xoay tạo được khi quay $K$ xung quanh trục hoành là một số không phụ thuộc và giá trị của a và b nếu a và b thỏa mãn điều kiện sau

A. $b^{4} = 2 a^{3}$

B. $b^{4} = 2 a^{2}$

C. $b^{5} = a^{3}$

D. $b^{3} = a^{5}$

Xem đáp án

Câu 43:

Cho hình thang vuông ABCD có đường cao $AD=1$ , đáy nhỏ AB=1, đáy lớn $CD = 2$ . Cho hình thang đó quay quanh AB ta được khối tròn xoay có thể tích bằng

A. $\frac{4 π}{3} (dvtt)$

B. $\frac{5 π}{3} (dvtt)$

C. $\frac{π}{3} (dvtt)$

D. $\frac{2 π}{3} (dvtt)$

Xem đáp án

Đáp án B

Khi quay hình thang quanh AB, ta được khối tròn quay có thể tích băng thể tích hình trụ bán kính đáy AD, chiều cao CD trừ đi thể tích hình nón có bán kính đáy AD, chiều cao CE.

Dễ dàng tính được CE=1.

Ta có

Câu 44:

Trong mặt phẳng tọa độ $Oxy$ , gọi M là điểm biểu diễn số phức $z = 1 - 2 i$ , N là điểm biểu diễn số phức $z^{'} = \frac{1 - i}{2} z$ . Tính diện tích tam giác OMM'

A. $\frac{10}{3}$

B. $\frac{5}{2}$

C. $\frac{5}{4}$

D. $\frac{3}{5}$

Xem đáp án

Câu 45:

Trong không gian với hệ tọa độ $Oxyz$ , cho hai điểm $M (1; 2; 3)$ và $N (2; 1; - 2)$ . Phương trình mặt phẳng $(P)$ chứa hai điểm $M, N$ và song song với trục Ox là

A. $- 5 y - z + 8 = 0$

B. $- 5 y + z + 7 = 0$

C. $- 5 y + z - 7 = 0$

D. $- 5 y - z + 5 = 0$

Xem đáp án

Câu 46:

Một cái ly có dạng hình nón như sau

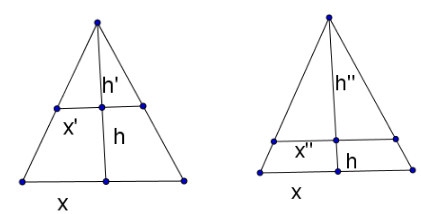
Người ta đổ một lượng nước vào ly sao cho chiều cao của lượng nước bằng $\frac{1}{2}$ chiều cao của ly. Nếu bịt kín miệng ly rồi lộn ngược ly lên thì tỷ lệ chiều cao của nước và chiều cao của ly bằng bao nhiêu?

A. $\frac{1}{8}$

B. $\frac{2 - \sqrt[3]{7}}{2}$

C. $\frac{1}{2}$

D. $\frac{2 - \sqrt[3]{4}}{2}$

Xem đáp án

Đáp án B

Minh họa trước và sau khi úp ly như hình vẽ.

Câu 47:

Trong không gian với hệ tọa độ Oxyz, cho sáu điểm $A (0; 1; 2), B (2; - 1; - 2);$ $C (3; 1; 2), A^{'}, B^{'}, C^{'}$ thỏa mãn $\vec{{AA}^{'}} + \vec{{BB}^{'}} + \vec{{CC}^{'}} = \vec{0} .$ Gọi G' là trọng tâm tam giác A'B'C' thì G' có tọa độ là

A. $(5; 1; 2)$

B. $(\frac{5}{3}; \frac{1}{3}; \frac{4}{3})$

C. $(\frac{5}{3}; \frac{1}{3}; \frac{2}{3})$

D. $(\frac{1}{3}; \frac{2}{3}; \frac{2}{3})$

Xem đáp án

Câu 48:

Giải bất phương trình $6^{{\log^{2}}_{6} x} + x^{\log_{6} x} \leq 12$

A. $0 \leq x \leq 6$

B. $(- \infty; \frac{1}{6}) \cup (6; + \infty)$

C. $\frac{1}{6} \leq x \leq 6$

D. $0 \leq x \leq \frac{1}{6}$

Xem đáp án

Câu 49:

Gọi $x_{1}$ là nghiệm của phương trình ${log}_{2} (1 + \sqrt{x}) = \log_{3} x$ . Tính giá trị biểu thức $A = {x_{1}}^{2} + 2 x_{1} .$

A.15

B. 9

C. 171

D. 99

Xem đáp án

Câu 50:

Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, cạnh bên SA=2a. Góc giữa (SAB) và đáy bằng $60^{o}$ , góc giữa (SBC) và đáy bằng $45^{o}$ . Tính thể tích khối chóp S.ABCD biết chân đường cao hạ từ S nằm trong hình vuông ABCD.

A. $\frac{16 a^{3}}{7} (dvtt)$

B. $\frac{16 a^{3}}{21} (dvtt)$

C. $2 a^{3} (dvtt)$

D. $\sqrt{2} a^{3} (dvtt)$

Xem đáp án

CHỌN BỘ SÁCH BẠN MUỐN XEM

Tổng hợp đề thi thptqg môn Toán cực hay mới nhất

Tổng hợp đề thi thptqg môn Toán cực hay mới nhất - đề 5

Danh sách câu hỏi

Bài thi liên quan