50 câu hỏi trắc nghiệm thuộc Tổng hợp đề thi thptqg môn Toán cực hay mới nhất - đề 14

Câu 1:

Thể tích khối tròn xoay được giới hạn bởi đường $y = \sqrt{1 - x^{2}}, y = 0, x = 0$ khi quay quanh trục Ox không được tính bằng công thức nào sau đây?

A. $π {(x - \frac{x^{3}}{3})|}_{0}^{1}$

B. $π \int_{0}^{1} (1 - x^{2}) dx$

C. $π \int_{0}^{1} {(1 - x^{2})}^{2} dx$

D. $\frac{2 π}{3}$

Xem đáp án

Câu 2:

Diện tích hình tròn lớn của một hình cầu là 2a . Một mặt phẳng (P) cắt hình cầu đó theo đường tròn nhỏ có bán kính r và có diện tích bằng một nửa diện tích đường tròn lớn. Biết bán kính của hình cầu là R, chọn đáp án đúng:

A. $R = \frac{2 r}{\sqrt{3}}$

B. $R = r \sqrt{2}$

C. $R = 2 \sqrt{2} r$

D. $R = 2 r$

Xem đáp án

Câu 3:

$\lim \frac{n^{2} - 3 n^{3} + 1}{2 n^{3} + 5 n - 2}$ bằng

A. $\frac{1}{2}$

B. 0

C. $- \frac{3}{2}$

D. $\frac{1}{5}$

Xem đáp án

Đáp án C

$\lim \frac{n^{2} - 3 n^{3} + 1}{2 n^{3} + 5 n - 2} = \frac{- 3}{2}$

Câu 4:

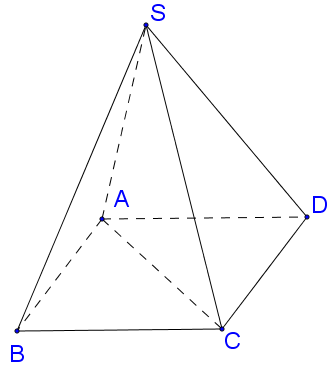
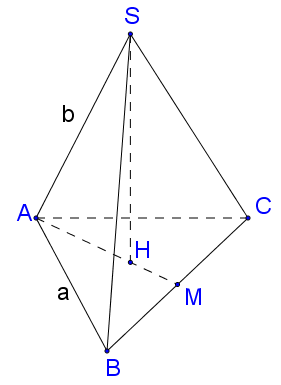
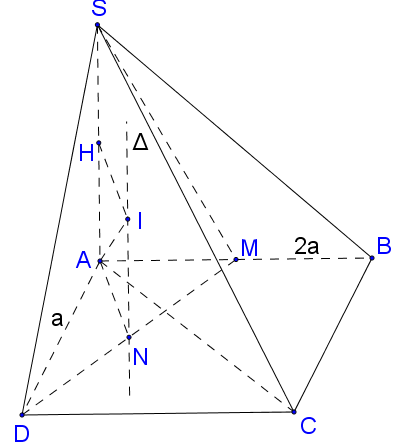
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, $AD = a, AB = 2 a$ , cạnh bên $SA = a \sqrt{3}$ và vuông góc với mặt phẳng đáy (ABCD). Gọi M là trung điểm AB. Tính bán kính hình cầu ngoại tiếp hình chóp S.AMD.

A. $\frac{a \sqrt{5}}{2}$

B. $\frac{a \sqrt{5}}{4}$

C. $\frac{a \sqrt{2}}{2}$

D. $\frac{a \sqrt{3}}{2}$

Xem đáp án

Đáp án A

Gọi N là trung điểm của MD, khi đó N là tâm đường tròn ngoại tiếp tam giác vuông ADM.

Dựng đường thẳng Δ đi qua N và song song với SA⇒Δ là trục đường tròn ngoại tiếp tam giác ADM.

Dựng mặt phẳng trung trực (P) của SA, $(P) \cap Δ = I$ , khi đó I là tâm của mặt cầu ngoại tiếp hình chóp SADM, bán kính $R = IA$ .

Câu 5:

Biết $\int_{0}^{1} (e^{x} - \frac{2}{x + 1}) dx = e + aln 2 + b$ $(a, b \in ℤ)$ . Tính giá trị biểu thức $P = 2 a + b$ .

A. 5

B. -5

C. -4

D. 3

Xem đáp án

Câu 6:

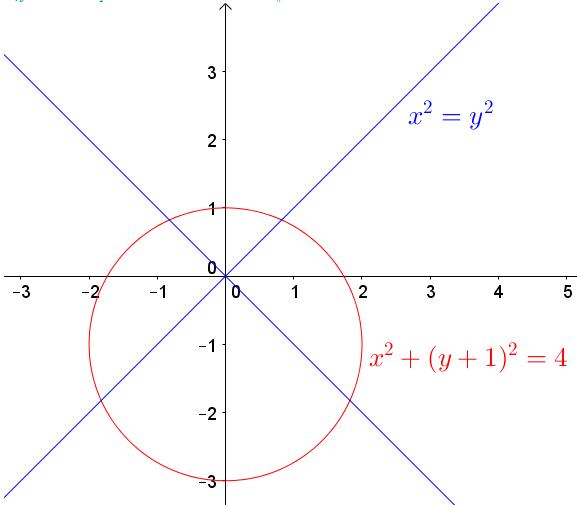
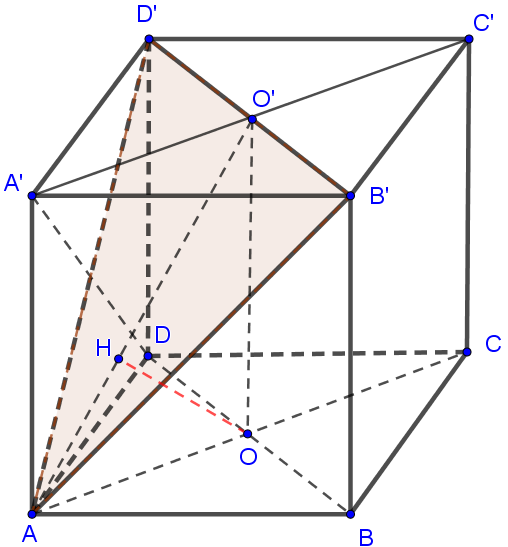
Tập hợp các điểm có tọa độ $(x; y; z)$ sao cho $0 \leq x \leq 3, - 1 \leq y \leq 5, - 2 \leq z \leq 2$ là tập hợp của một khối đa diện (lồi) có một tâm đối xứng. Tìm tọa độ tâm đối xứng đó.

A. $(\frac{3}{2}; 3; 2)$

B. $(2; 3; 2)$

C. $(- 1; 0; 2)$

D. $(\frac{3}{2}; 2; 0)$

Xem đáp án

Đáp án D

Tập hợp các điểm thỏa mãn yêu cầu bài toán là khối hộp chữ nhật với các kích thước là $(x, y, z) = (3, 6, 4)$ .

Tâm đối xứng I của khổi hộp chính là giao điểm của ba mặt phẳng trung trực tương ứng với 3 cạnh xuất phát từ một đỉnh của khối hộp. Do đó $I (\frac{0 + 3}{2}; \frac{- 1 + 5}{2}; \frac{- 2 + 2}{2}) = (\frac{3}{2}; 2; 0)$ .

Câu 7:

Rút gọn biểu thức $P = \frac{\sqrt[3]{a^{2}}}{a^{2}}$ .

A. $a^{\frac{3}{4}}$

B. $a^{\frac{- 1}{2}}$

C. $a^{\frac{- 4}{3}}$

D. $a^{\frac{1}{3}}$

Xem đáp án

Đáp án C

$P = \frac{a^{\frac{2}{3}}}{a^{2}} = a^{\frac{- 4}{3}}$

Câu 8:

Có 8 cái bút khác nhau và 7 quyển vở khác nhau được gói trong 15 hộp. Một học sinh được chọn bất kì hai hộp. Xác suất để học sinh đó chọn được một cặp bút và vở là

A. $\frac{8}{15}$

B. $\frac{8}{105}$

C. $\frac{1}{15}$

D. $\frac{1}{7}$

Xem đáp án

Đáp án A

Xác suất cần tính là $\frac{C_{8}^{1} C_{7}^{1}}{C_{15}^{2}} = \frac{8}{15}$

Câu 9:

Cho cấp số cộng $(u_{n})$ có $u_{1} = - 2$ và công sai $d = 3$ . Số hạng $u_{10}$ là

A. 25

B. 26

C. 27

D. 28

Xem đáp án

Đáp án A

$u_{n} = u_{1} + (n - 1) d \Rightarrow u_{10} = - 2 + 9 .3 = 25$

Câu 10:

Số nghiệm nguyên dương của bất phương trình $9^{x + 1} \leq {(\frac{1}{3})}^{- \frac{4}{x}}$ là

A. 2

B. 1

C. Vô số nghiệm nguyên dương

D. 3

Xem đáp án

Câu 11:

Cho hàm số f(x) có đạo hàm trên đoạn $[- 5; 5]$ . Biết $f (- 2) = 3$ và $f (3) = 2$ , tính $I = \int_{- 2}^{3} f^{'} (x) dx$ .

A. 1

B. 5

C. -1

D. 0

Xem đáp án

Câu 12:

Tìm giá trị lớn nhất của hàm số $y = \log_{2} (2 x - x^{2})$ .

A. 1

B. 2

C. 0

D. Hàm số không tồn tại giá trị lớn nhất

Xem đáp án

Câu 13:

Cho $\int_{- 1 / 2}^{1} f (x) d x = 3$ . Tính tích phân $I = \int_{0}^{π / 3} f (\cos 2 x) \sin 2 xdx$ .

A. $\frac{2}{3}$

B. 3

C. -3

D. $\frac{3}{2}$

Xem đáp án

Câu 14:

Trong không gian với hệ tọa độ Oxyz, cho các véctơ $\vec{a} = (1; - 3; 0), \vec{b} = (0; 9; - 3),$ $\vec{c} = (5; 5; 5), \vec{d} = (2; 3; - 3)$ . Biết $\vec{d} = x . \vec{a} + y . \vec{b} + z . \vec{c}$ . Tính tổng $x + y + z .$

A. 5

B. 4

C. 6

D. 3

Xem đáp án

Câu 15:

Cho khối chóp S.ABCD có thể tích bằng $64 {cm}^{3}$ . Mặt bên SAB là tam giác đều cạnh bằng 4cm và đáy ABCD là hình bình hành. Tính khoảng cách giữa hai đường thẳng SA và CD.

A. $2 \sqrt{3}$

B. $6 \sqrt{3}$

C. $4 \sqrt{3}$

D. $8 \sqrt{3}$

Xem đáp án

Câu 16:

Cho hàm số $y = x^{3} - 3 x^{2} - m$ . Tìm m để hàm số có giá trị cực đại và giá trị cực tiểu trái dấu nhau.

A. $0 < m < 4$

B. $m > 4$ hoặc $m < 0$

C. $m > 0$ hoặc $m < - 4$

D. $- 4 < m < 0$

Xem đáp án

Câu 17:

Tính đạo hàm của hàm số $y = \ln (\sqrt{x^{2} + 1} - x)$ .

A. $y^{'} = - \frac{1}{\sqrt{x^{2} + 1}}$

B. $y^{'} = \frac{1}{\sqrt{x^{2} + 1}}$

C. $y^{'} = \frac{x}{\sqrt{x^{2} + 1}}$

D. $y^{'} = - \frac{1}{\sqrt{x^{2} + 1} - x}$

Xem đáp án

Câu 18:

Các đường tiệm cận của đồ thị hàm số $y = \frac{2 x - 2}{1 + 3 x}$ tạo với hai trục tọa độ một hình chữ nhật có diện tích bằng

A. $\frac{2}{9}$

B. $\frac{1}{9}$

C. $\frac{1}{3}$

D. $\frac{3}{2}$

Xem đáp án

Đáp án A

Đồ thị hàm số có đường tiệm cận ngang là $y = \frac{2}{3}$ và tiệm cận đứng là $x = - \frac{1}{3}$ .

Do đó diện tích hình chữ nhật cần tính là: $S = |\frac{2}{3} . (- \frac{1}{3})| = \frac{2}{9}$ .

Câu 19:

Cho $I = \int_{1}^{a} (x^{2} - 2 x + 1) dx = \frac{1}{3}$ , khi đó giá trị của a là

A. a = 0

B. a = 2

C. a = 3

D. a = 1

Xem đáp án

Câu 20:

Tập xác định của hàm số $y = {(- e^{2 x} + 6 e^{x} - 5)}^{\frac{1}{3}}$ là

A. $x < 0$

B. $x > \ln 5$

C. $0 < x < e^{5}$

D. $0 < x < \ln 5$

Xem đáp án

Đáp án C

Câu 21:

Tổng phần thực và phần ảo của số phức $z = (1 - 2 i) (- 2 + 3 i)$ là

A. 11

B. -3

C. 4+7i

D. 4-7i

Xem đáp án

Câu 22:

Cho hai điểm $A (1; 1; 2), B (2; 1; - 2)$ . Mặt cầu có tâm thuộc trục hoành và đi qua hai điểm A, B có phương trình là

A. ${(x - \frac{3}{2})}^{2} + y^{2} + z^{2} = \frac{21}{2}$

B. ${(x - \frac{3}{2})}^{2} + y^{2} + z^{2} = \frac{21}{4}$

C. ${(x + \frac{3}{2})}^{2} + y^{2} + z^{2} = \frac{21}{4}$

D. ${(x + \frac{3}{2})}^{2} + y^{2} + z^{2} = \frac{21}{2}$

Xem đáp án

Câu 23:

Cho ba số thực dương a,b,c khác 1. Đồ thị các hàm số $y = \log_{a} x, y = \log_{b} x$ và $y = \log_{c} x$ được cho trong hình vẽ sau:

A. $c < b < a$

B. $a < b < c$

C. $a < c < b$

D. $b < c < a$

Xem đáp án

Câu 24:

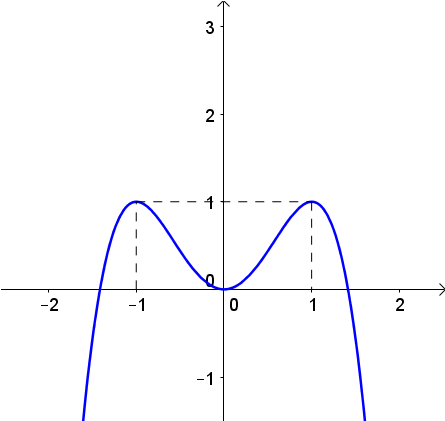
Số điểm có tọa độ nguyên nằm trên đồ thị hàm số $y = \frac{3 x + 5}{x + 1}$ là

A. 2

B. 4

C. 1

D. 3

Xem đáp án

Đáp án B

Yêu cầu bài toán tương đương với “Tìm x nguyên để y nhận giá trị nguyên”.

Ta có

Câu 25:

Nếu $\log_{a} b = m$ thì $\log_{a} a^{3} b^{4}$ bằng

A. $3 + \frac{4}{m}$

B. $4 + 3 m$

C. $12 m$

D. $3 + 4 m$

Xem đáp án

Câu 26:

Giá trị cực đại của hàm số $y = \sqrt{2} x + \cos 2 x$ trên $[0; \frac{π}{4}]$ là

A. $y_{\min} = \frac{π}{4}; y_{\max} = 1$

B. $y_{\min} = \frac{π \sqrt{2}}{8} - \frac{\sqrt{2}}{2}; y_{\max} = \frac{π}{4}$

C. $y_{\min} = 1; y_{\max} = \frac{π \sqrt{2}}{8} + \frac{\sqrt{2}}{2}$

D. $y_{\min} = \frac{π \sqrt{2}}{8}; y_{\max} = \frac{π \sqrt{2}}{8} + \frac{\sqrt{2}}{2}$

Xem đáp án

Câu 27:

Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = f (x) = sinxcosx$ , đường thẳng $y = 0, x = 0$ và $x = \frac{π}{2}$

A. 1

B. $\frac{1}{2}$

C. $\frac{π}{2}$

D. $\frac{1}{4}$

Xem đáp án

Câu 28:

Một hộp đựng 10 viên bi có kích thước khác nhau, trong đó có 7 viên bi màu đỏ và 3 viên bi màu xanh. Chọn ngẫu nhiên 2 viên bi. Xác suất để 2 viên bi được chọn có đúng một viên bi màu xanh bằng

A. $\frac{1}{15}$

B. $\frac{8}{15}$

C. $\frac{7}{15}$

D. $\frac{2}{15}$

Xem đáp án

Đáp án C

Xác suất cần tính là $\frac{C_{7}^{1} C_{3}^{1}}{C_{10}^{2}} = \frac{7}{15}$

Câu 29:

Nếu số phức $z \neq 1$ thỏa mãn $|z| = 1$ thì phần thực của số phức $\frac{1}{1 - z}$ bằng

A. 1

B. $- \frac{1}{2}$

C. $\frac{1}{2}$

D. 2

Xem đáp án

Câu 30:

Cho hàm số $y = x^{4} - 2 x^{2} + m$ . Tìm các giá trị thực của m để đồ thị hàm số có ba điểm cực trị tạo thành một tam giác vuông cân.

A. $m = 1$

B. $m = \pm 1$

C. $m \in ℝ$

D. $m = 0$

Xem đáp án

Câu 31:

Cho hình chữ nhật ABCD có cạnh $AB = 4, AD = 6$ . Gọi M, N lần lượt là trung điểm của AD, BC. Tính thể tích hình trụ tròn xoay được tạo thành khi quay hình chữ nhật ABCD quanh cạnh MN.

A. $18 π$

B. $12 π$

C. $36 π$

D. $24 π$

Xem đáp án

Câu 32:

Trong không gian với hệ tọa độ Oxyz, cho điểm $A (0; 0; - 1)$ và đường thẳng $d : \{\begin{cases} x = t \\ y = - 1 + 2 t \\ z = - t \end{cases}$

Gọi (P) là mặt phẳng chứa đường thẳng d và đi qua A. Viết phương trình mặt cầu tâm O tiếp xúc với mặt phẳng (P).

A. $(S) : x^{2} + y^{2} + z^{2} = \sqrt{3}$

B. $(S) : x^{2} + y^{2} + z^{2} = \frac{1}{\sqrt{3}}$

C. $(S) : x^{2} + y^{2} + z^{2} = 3$

D. $(S) : x^{2} + y^{2} + z^{2} = \frac{1}{3}$

Xem đáp án

Câu 33:

Cho A,B,C là các điểm biểu diễn số phức z thỏa mãn $z^{3} - i = 0$ . Tìm phát biểu sai

A. Tam giác ABC là tam giác đều

B. Tam giác ABC có trọng tâm $O (0; 0)$

C. Tâm đường tròn ngoại tiếp tam giác ABC nằm trên trục tung

D. Diện tích tam giác ABC bằng $\frac{3 \sqrt{3}}{2}$

Xem đáp án

Câu 34:

Cho hàm số y=f(x) xác định trên R∖{1}, liên tục trên các khoảng xác định của nó và có bảng biến thiên như hình vẽ:

Khẳng định nào sau đây là đúng?

A. Giá trị lớn nhất của hàm số là −22

B. Đồ thị hàm số có 3 đường tiệm cận

C. Đồ thị hàm số có 2 giá trị cực tiểu

D. Hàm số nghịch biến trên khoảng (−1;+∞)

Xem đáp án

Câu 35:

Cho hình chóp tam giác đều SABC cạnh đáy bằng a và cạnh bên bằng b. Tính thể tích khối chóp S.ABC.

A. $\frac{a^{2} \sqrt{3 b^{2} - a^{2}}}{12}$

B. $\frac{a^{2} \sqrt{3 b^{2} - a^{2}}}{4}$

C. $\frac{a^{2} \sqrt{b^{2} - a^{2}}}{4}$

D. $\frac{a^{2} \sqrt{b^{2} - a^{2}}}{12}$

Xem đáp án

Câu 36:

Hình vẽ bên giống với đồ thị của hàm số nào nhất?

A. $y = x^{4} + 2 x^{2}$

B. $y = - x^{4} + x^{2}$

C. $y = x^{4} + x^{2}$

D. $y = - x^{4} + 2 x^{2}$

Xem đáp án

Câu 37:

Họ nguyên hàm F(x) của hàm số f(x) = xln⁡x là

A. $F (x) = \int^{} xlnxdx$

B. $F (x) = \int^{} x^{2} . lnxdx$

C. $F (x) = \int 2^{} x^{2} . lnxdx$

D. $F (x) = \int 2^{} x . lnxdx$

Xem đáp án

Câu 38:

Cho hàm số y=f(x) có đạo hàm là f′(x)=(x−1)(x−2)2(x−3). Số điểm cực trị của hàm số là

A. 3

B. 1

C. 2

D. 0

Xem đáp án

Câu 39:

Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA=SB=SC=2a. Cosin của góc giữa đường thẳng SC và mặt phẳng (ABC) bằng

A. $\frac{3}{\sqrt{6}}$

B. $\frac{2}{\sqrt{5}}$

C. $\frac{2}{\sqrt{6}}$

D. $\frac{3}{\sqrt{5}}$

Xem đáp án

Câu 40:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm $A (1; 2; 3), B (3; - 2; 1)$ và mặt phẳng $(P) : x + y - z - 3 = 0$ . Gọi M, N lần lượt là hình chiếu của A và B lên mặt phẳng (P). Tính độ dài đoạn thẳng MN.

A. $2 \sqrt{6}$

B. $4 \sqrt{3}$

C. 24

D. $3 \sqrt{2}$

Xem đáp án

Câu 41:

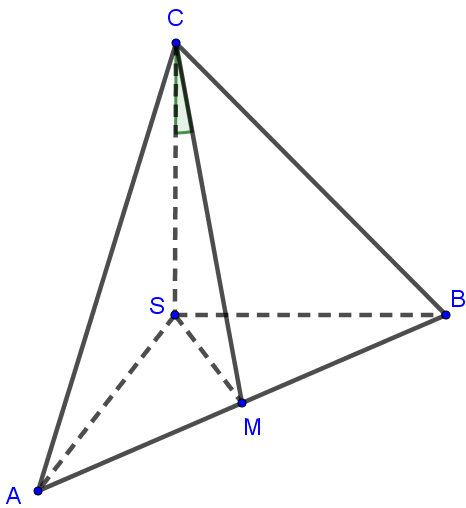
Cho hình lăng trụ ABC.A′B′C′ có đáy ABC là tam giác đều cạnh 2a. Hình chiếu vuông góc của A′ xuống mặt phẳng ABC trùng với trung điểm của cạnh AB. Mặt bên (ACC′A′) tạo với đáy một góc $60^{0}$ . Tính thể tích khối lăng trụ ABC.A′B′C′.

A. $\frac{3 a^{3}}{2}$

B. $\frac{3 a^{3} \sqrt{3}}{2}$

C. $\frac{a^{3} \sqrt{3}}{2}$

D. $\frac{a^{3} \sqrt{3}}{3}$

Xem đáp án

Đáp án B

Gọi M, N lần lượt là trung điểm của AC và AM.

Khi đó ΔAHM là tam giác đều và $NH ⊥ AC$ .

Câu 42:

Biết n là số nguyên dương thỏa mãn $C_{n}^{n - 1} + C_{n}^{n - 2} = 78$ . Số hạng chứa $x^{4}$ trong khai triển ${(x^{2} - \frac{2}{x})}^{n}$ là

A. 126720

B. $- 25344 x^{4}$

C. $25344 x^{4}$

D. $- 112640$

Xem đáp án

Câu 43:

Giá trị lớn nhất của hàm số $y = 2 \cos^{2} x - \sin 2 x + 5$ là

A. $6 + \sqrt{2}$

B. $\sqrt{2}$

C. $- \sqrt{2}$

D. $6 - \sqrt{2}$

Xem đáp án

Câu 44:

Có bao nhiêu nghiệm phức z thỏa mãn $|z + i| = 2$ và $z^{2}$ là số thuần ảo?

A. 2

B. 4

C. 1

D. 3

Xem đáp án

Câu 45:

Cho hàm số $y = \frac{x^{2} + 2 x}{x - m}$ . Tìm m để hàm số đồng biến trên $(- 1; + \infty)$

A. $m \in (- \infty; - 1]$

B. $m \leq 0$

C. $m \geq - 1$

D. $m > - 1$

Xem đáp án

Câu 46:

Cho số phức z thỏa mãn $|z + i + 1| = |\bar{z} - 2 i|$ . Tìm giá trị nhỏ nhất của mô đun của số phức z.

A. $\frac{1}{\sqrt{2}}$

B. $\sqrt{2}$

C. $\frac{1}{2}$

D. $\frac{1}{4}$

Xem đáp án

Câu 47:

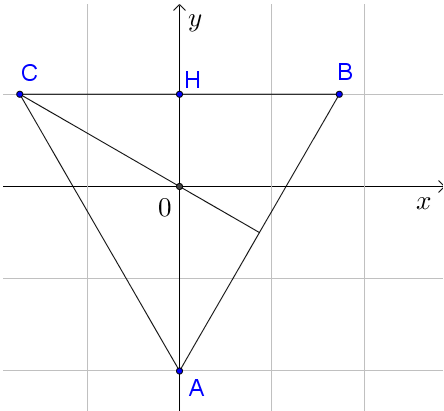
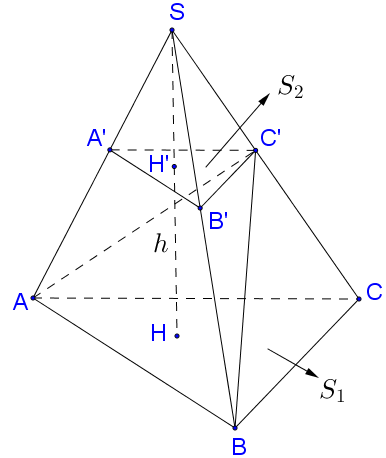
Cho hình chóp cụt ABC.A′B′C′ có hai đáy ABC và A′B′C′ có diện tích lần lượt là $S_{1}$ và $S_{2}$ . Mặt phẳng (ABC′) chia hình chóp cụt thành hai phần, Tính tỉ số thể tích hai phần đó.

A. $\frac{S_{2}}{S_{1} + \sqrt{S_{1} S_{2}}}$

B. $\frac{S_{1}}{S_{2} + \sqrt{S_{1} S_{2}}}$

C. $\frac{S_{1}}{S_{2} - \sqrt{S_{1} S_{2}}}$

D. $\frac{S_{2}}{S_{1} - \sqrt{S_{1} S_{2}}}$

Xem đáp án

Đáp án B

Gọi HH' = h là khoảng cách giữa hai mặt phẳng đáy, S là đỉnh của hình chóp cụt (hình vẽ).

Mặt phẳng (ABC′) chia hình chóp cụt thành 2 phần: C′ABC và ABB′A′C′ có thể tích lần lượt là $V_{1}$ và $V_{2}$ .

$V_{1} = \frac{1}{3} h S$

Gọi V là thể tích khối chóp cụt ABCA′B′C′

Câu 48:

Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Khoảng cách từ điểm D đến mặt phẳng (AD’B’) bằng

A. $a$

B. $\frac{a \sqrt{2}}{2}$

C. $\frac{a \sqrt{3}}{3}$

D. $\frac{a \sqrt{6}}{3}$

Xem đáp án

Câu 49:

Số cách chia 10 phần quà giống nhau cho 3 bạn sao cho ai cũng có ít nhất 2 phần quà là

A. 30

B. 15

C. 21

D. 10

Xem đáp án

Đáp án B

Để đảm bảo mỗi bạn có ít nhất 2 phần quà, ta chia cho 3 bạn mỗi bạn 2 phần quà có 1 cách (vì các phần quà là như nhau)

Như vậy bài toán trở thành: Có 4 phần quà, chia cho 3 bạn, có thể có bạn không có phần nào.

Xếp 4 phần quà theo hàng ngang, để chia thành 3 nhóm ta cần 2 cách ngăn. Vậy bài toán quy về trong 6 vị trí (quà và vách ngăn), chọn 2 vị trí để đặt vách ngăn. Vậy số cách chọn là $C_{6}^{2} = 15$ cách.

Câu 50:

Trong không gian cho 2n điểm phân biệt $n \geq 4, \in N$ , trong đó không có ba điểm nào thẳng hàng và trong 2n điểm đó có đúng n điểm cùng nằm trên một mặt phẳng. Tìm tất cả các giá trị của n sao cho từ 2n điểm đã cho tạo ra đúng 505 mặt phẳng phân biệt?

A. 12

B. 7

C. 24

D. 8

Xem đáp án

Đáp án D

Số cách chọn ra 3 điểm từ 2n điểm đã cho là $C_{2 n}^{3}$ suy ra số mặt phẳng được tạo ra là $C_{2 n}^{3}$ .

Do trong 2n điểm đã cho có n điểm đồng phẳng nên có $C_{n}^{3}$ mặt phẳng trùng nhau.

Suy ra số mặt phẳng được tạo thành từ 2n điểm đã cho là $C_{2 n}^{3} - C_{n}^{3} + 1$ .

CHỌN BỘ SÁCH BẠN MUỐN XEM

Tổng hợp đề thi thptqg môn Toán cực hay mới nhất

Tổng hợp đề thi thptqg môn Toán cực hay mới nhất - đề 14

Danh sách câu hỏi

Bài thi liên quan