50 câu hỏi trắc nghiệm thuộc Tổng hợp đề thi thptqg môn Toán cực hay mới nhất - đề 18

Câu 1:

Cho đường thẳng $d : y = - 2 x + 1$ . Đồ thị của hàm số $y = x^{3} - 3 mx + 1$ có hai điểm cực trị nằm trên đường thẳng d khi

A. m = 0

B. m = 2

C. m = $\sqrt{2}$

D. m = 1

Xem đáp án

Câu 2:

Một người gửi tiết kiệm 300 triệu đồng loại kì hạn 6 tháng vào ngân hàng với lãi suất 10%/năm thì sau 9 năm 9 tháng người đó nhận đc bao nhiêu tiền cả vốn lẫn lãi, biết người đó không rút lãi ở các định kì trước. Nếu có rút trước thời hạn thì ngân hàng trả lãi suất loại không kì hạn là 0.015%/ ngày 1tháng = 30ngày.

A. 0,978 tỉ đồng

B. 1,062 tỉ đồng

C. 1,147 tỉ đồng

D. 1,001 tỉ đồng

Xem đáp án

Đáp án B

Lãi suất với kì hạn 6 tháng là $r = \frac{10 %}{2} = 5 %$

Trong 9 năm 6 tháng thì người đó nhận được số tiền cả gốc lẫn lãi là $300 {(1 + r)}^{9 \times 2 + 1}$

Ba tháng còn lại là người đó rút trước thời gian và tính theo lãi suất không kì hạn là 0,015%/ ngày. Do đó, số tiền nhận được trong 3 tháng này là

Vậy sau 9 năm 9 tháng người đó nhận được số tiền là

$300 {(1 + r)}^{9 \times 2 + 1} + 300 {(1 + 0, 015 %)}^{3 \times 30}$

$\approx 1, 062$ tỉ đồng.

Câu 3:

Cho hình chữ nhật ABCD có $AB = 2, AD = 4$ . Tính thể tích V của khối trụ tạo thành khi quay hình chữ nhật ABCD quanh trục CD

A. $24 π$

B. $\frac{32 π}{3}$

C. $32 π$

D. $16 π$

Xem đáp án

Đáp án C

Câu 4:

Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng $d : \frac{x}{2} = \frac{y - 1}{2} = \frac{z}{- 1}$ và điểm A(1;0;0). Viết phương trình đường thẳng đi qua A và song song với đường thẳng d.

A. $\frac{x - 1}{1} = \frac{y}{1} = \frac{z}{4}$

B. $\frac{x + 1}{1} = \frac{y}{1} = \frac{z}{4}$

C. $\frac{x + 1}{2} = \frac{y}{2} = \frac{z}{- 1}$

D. $\frac{x - 1}{2} = \frac{y}{2} = \frac{z}{- 1}$

Xem đáp án

Câu 5:

Tìm các giá trị thực của m để phương trình $lnx + \ln (1 - x) = m$ có hai nghiệm phân biệt thuộc khoảng (0;1).

A. $m \leq - 2 \ln 2$

B. $m > - 2 \ln 2$

C. $m < - 2 \ln 2$

D. $0 < m < 1$

Xem đáp án

Câu 6:

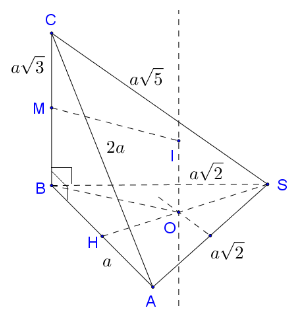
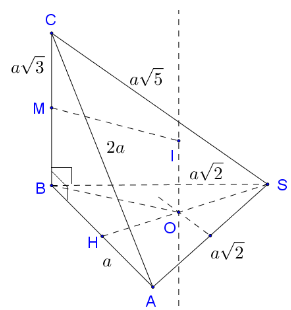
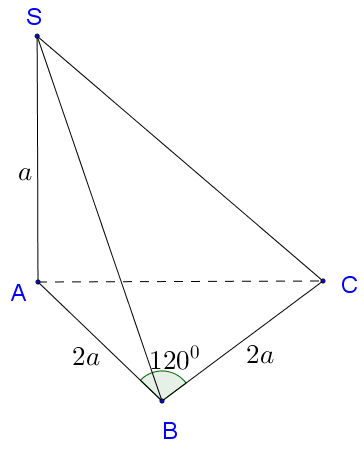
Cho hình chóp S.ABC có $SA = a, SA ⊥ (ABC)$ . Tam giác ABC có $AB = BC = 2 a$ , $\hat{ABC} = 120^{0}$ . Tính khoảng cách từ A đến mặt phẳng (SBC).

A. $\frac{a \sqrt{3}}{4}$

B. $\frac{a \sqrt{3}}{2}$

C. $\frac{a \sqrt{3}}{3}$

D. $a \sqrt{2}$

Xem đáp án

Đáp án B

Câu 7:

Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng d có phương trình $\frac{x - 1}{2} = \frac{y}{- 3} = \frac{z - 2}{0}$ và mặt phẳng $(P) : x + y = 0$ . Tìm tọa độ điểm M trên d có hoành độ dương sao cho khoảng cách từ M đến (P) bằng $\sqrt{2}$ .

A. $M (3; - 3; 2)$

B. $M (7; - 9; 2)$

C. $M (5; - 6; 2)$

D. $M (- 1; 3; 2)$

Xem đáp án

Câu 8:

Cho hàm số $y = {ax}^{3} + {bx}^{2} + cx + d$ , $(a \neq 0)$ có đồ thị như hình vẽ sau. Khẳng định nào sau đây là đúng?

A. $a > 0; b^{2} - 3 ac = 0$

B. $a < 0; b^{2} - 3 ac \leq 0$

C. $a < 0; b^{2} - 3 ac = 0$

D. $a > 0; b^{2} - 3 ac \leq 0$

Xem đáp án

Câu 9:

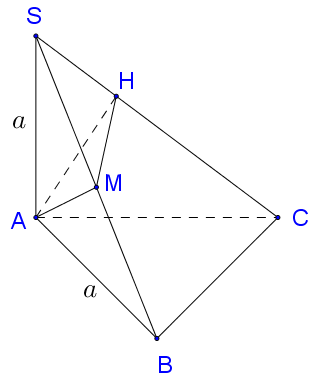
Cho hình chóp S.ABC có SA vuông góc với đáy, SA = a, tam giác ABC vuông cân, Ab = BC = a là trung điểm của SB, H là chân đường cao hạ từ A của tam giác SAC. Tính thể tích hình chóp S.AMH.

A. $\frac{a^{3}}{9}$

B. $\frac{a^{3}}{12}$

C. $\frac{a^{3}}{27}$

D. $\frac{a^{3}}{36}$

Xem đáp án

Đáp án D

Câu 10:

Giá trị của tích phân $I = \int_{0}^{π} xsinxdx$ được biểu diễn dưới dạng $I = aπ + b$ . Khi đó tổng a+b bằng

A. $π - 1$

B. 0

C. 1

D. $2 π$

Xem đáp án

Câu 11:

Cho hàm số f(x) liên tục trên [1;4] và thỏa mãn điều kiện $\int_{1}^{2} f (x) dx = 1$ , $\int_{1}^{2} f (2 x - 1) dx = 2$ . Tính giá trị của biểu thức $I=_{2}^{3} f (x) d x$ .

A. 3

B. -1

C. 1

D. 0

Xem đáp án

Câu 12:

Cho Parabol $(P) : y = 2 x^{2}$ . Gọi d là tiếp tuyến với (P) tại điểm có hoành độ bằng 2. Tính diện tích hình phẳng giới hạn bởi đồ thị (P), đường thẳng d và đường thẳng x=1.

A. $\frac{2}{3}$

B. $\frac{1}{2}$

C. $\frac{1}{3}$

D. $\frac{3}{2}$

Xem đáp án

Câu 13:

Tìm tất cả các giá trị thực của tham số m để hàm số $y = {mx}^{3} - 3 mx + 1$ nghịch biến trên (1;+∞).

A. $m < 1$

B. $m < 0$

C. $m > 0$

D. $m \leq 0$

Xem đáp án

Câu 14:

Gọi A,B,C là điểm biểu diễn các số phức $z = 2 i; z = 2 + i; z = - 3 i$ . Khi đó diện tích tam giác ABC là

A. 7

B. 5

C. 6

D. 4

Xem đáp án

Câu 15:

Tìm giá trị thực của tham số m để ba điểm cực trị của đồ thị hàm số $y = x^{4} - 2 (m + 1) x^{2} - m + 1$ là ba đỉnh của một tam giác vuông là

A. m = 0

B. m = 2

C. m = 1

D. m = -1

Xem đáp án

Câu 16:

Số các tổ hợp chập k của một tập hợp có n phần tử với $1 \leq k \leq n$ là

A. $\frac{k! (n - k)!}{n!}$

B. $\frac{A_{n}^{k}}{(n - k)!}$

C. $\frac{n!}{(n - k)!}$

D. $\frac{A_{n}^{k}}{k!}$

Xem đáp án

Đáp án D

Số các tổ hợp chập k của một tập hợp có n phần tử với $1 \leq k \leq n$ là $C_{n}^{k} = \frac{n!}{k! (n - k)!} = \frac{A_{n}^{k}}{k!}$

Câu 17:

Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng $(P) : x - y + z + 4 = 0$ và mặt cầu $(S) : x^{2} + {(y - 1)}^{2} + {(z - 3)}^{2} = 12$ . Khẳng định nào sau đây là đúng về vị trí tương đối của (P) và (S)?

A. Mặt phẳng (P) không cắt mặt cầu (S)

B. Mặt phẳng (P) tiếp xúc với mặt cầu (S)

C. Mặt phẳng (P) cắt mặt cầu (S)với giao tuyến là một đường tròn bán kính lớn nhất

D. Mặt phẳng (P) cắt mặt cầu (S)với giao tuyến là một đường tròn bán kính bằng $2 \sqrt{33}$

Xem đáp án

Câu 18:

Cho đa giác đều 2n đỉnh $(n \geq 2) .$ Hỏi có bao nhiêu hình chữ nhật có 4 đỉnh là 4 trong 2n đỉnh của đa giác.

A. $C_{2 n}^{2}$

B. $C_{n}^{4}$

C. $C_{2 n}^{4}$

D. $C_{n}^{2}$

Xem đáp án

Đáp án D

Đa giác đều 2n đỉnh có n đường chéo qua tâm. Cứ 2 đường chéo qua tâm tương ứng với 1 hình chữ nhật có 4 đỉnh là đỉnh của đa giác. Do đó số hình chữ nhật là $C_{n}^{2}$

Câu 19:

Cho hai số phức $z_{1} = 1 + \sqrt{3} i$ , $\bar{z_{2}} = - 3 + 2 i$ . Tính $|z_{1} + z_{2}|$

A. $\sqrt{11 - 4 \sqrt{3}}$

B. $\sqrt{11 + 4 \sqrt{3}}$

C. $\sqrt{11 - 2 \sqrt{3}}$

D. $\sqrt{11 + 2 \sqrt{3}}$

Xem đáp án

Câu 20:

Cho các số thực x,y,z thỏa mãn $y = 10^{\frac{1}{1 - logx}}$ , $z = 10^{\frac{1}{1 - logy}}$ . Mệnh đề nào sau đây là đúng?

A. $x = 10^{\frac{1}{1 - lnz}}$

B. $x = 10^{\frac{- 1}{1 - logz}}$

C. $x = 10^{\frac{1}{1 + \log z}}$

D. $x = 10^{\frac{1}{1 - logz}}$

Xem đáp án

Câu 21:

Tìm giá trị lớn nhất của hàm số $y = sinxcosx$ trên đoạn $[0; \frac{π}{2}]$ .

A. $y_{\max} = 1$

B. $y_{\max} = 0$

C. $y_{\max} = 2$

D. $y_{\max} = \frac{1}{2}$

Xem đáp án

Câu 22:

Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng $(P) : 2 y - z + 4 = 0$ và điểm M(−1;0;−1). Xác định tọa độ hình chiếu vuông góc của M lên mặt phẳng (P)

A. $H (- 1; 4; 3)$

B. $H (- 1; 0; 0)$

C. $H (- 1; - 2; 0)$

D. $H (- 1; 2; - 2)$

Xem đáp án

Câu 23:

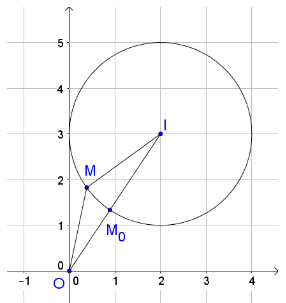
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu $(S) : {(x - 1)}^{2} + {(y - 1)}^{2} + z^{2} = 1$ . Tìm khoảng cách ngắn nhất từ gốc tọa độ O(0;0;0) đến mặt cầu (S).

A. $1 + \frac{1}{\sqrt{2}}$

B. $\sqrt{2} - 1$

C. $\sqrt{2} + 1$

D. $2 \sqrt{2} - 1$

Xem đáp án

Đáp án B

Mặt cầu (S) có tâm I(1;1;0) và bán kính R = 1

Câu 24:

Bảng biến thiên trong hình dưới đây giống với đồ thị của hàm số nào nhất?

A. $y = \frac{3 - x}{x - 1}$

B. $y = \frac{x - 2}{x - 1}$

C. $y = \frac{x + 2}{x - 1}$

D. $y = \frac{3 + x}{x - 1}$

Xem đáp án

Câu 25:

Cho F(x) là nguyên hàm của hàm số $f (x) = \frac{{(2 x + 1)}^{8}}{{(x + 1)}^{10}}$ thỏa mãn F(0)=1. Tìm hàm số F(x).

A. $F (x) = \frac{1}{8} {(\frac{2 x + 1}{x + 1})}^{8} + \frac{7}{8}$

B. $F (x) = \frac{1}{9} \ln (\frac{2 x + 1}{x + 1}) + \frac{8}{9}$

C. $F (x) = \frac{1}{9} {(\frac{2 x + 1}{x + 1})}^{9} + \frac{8}{9}$

D. $F (x) = - \frac{1}{9} {(\frac{x + 1}{2 x + 1})}^{9} + \frac{10}{9}$

Xem đáp án

Câu 26:

Phương trình sau đây có bao nhiêu nghiệm $\log_{2} x + \log_{3} x + \log_{4} x$ $+ . .. + \log_{10} x = 0$ ?

A. 1

B. 0

C. 2

D. 3

Xem đáp án

Câu 27:

Phần ảo của số phức $z = \frac{\sqrt{2} + 3 i}{1 - \sqrt{2} i}$ là

A. $- \frac{2 \sqrt{2}}{3}$

B. $\frac{5}{3}$

C. $- \frac{5}{3}$

D. $\frac{5}{3} i$

Xem đáp án

Câu 28:

Tập nghiệm của bất phương trình $\log_{2} (\log_{x} (x - 1)) \leq 1$ là

A. $x \in ℝ$

B. $x \neq 0$

C. $x \in \emptyset$

D. $x \in (1; + \infty)$

Xem đáp án

Câu 29:

Tiếp tuyến của đồ thị hàm số $y = 4 x^{4} - 2 x^{2} + 1$ tại điểm có hoành độ bằng 1 có phương trình

A. $y = 12 x - 12$

B. $y = 4 x - 1$

C. $y = - 9$

D. $y = 12 x - 9$

Xem đáp án

Câu 30:

Hàm số $F (x) = \log_{2} x + \frac{1}{e^{x}} + x^{2} + C$ là nguyên hàm của hàm số nào sau đây?

A. $f (x) = \frac{1}{xln 2} - \frac{1}{e^{x}} + 2 x$

B. $f (x) = \frac{1}{x} - \frac{1}{e^{x}} + 2 x$

C. $f (x) = \frac{1}{xln 2} + \frac{1}{e^{x}} + 2 x$

D. $f (x) = \frac{\ln 2}{x} - \frac{1}{e^{x}} + 2 x$

Xem đáp án

Câu 31:

Tìm số phức z có phần ảo dương thỏa mãn $\bar{z} - \frac{3 - 2 i}{z} - 2 i = 0$ . Khi đó |z| bằng

A. $|z| = \sqrt{5 - 2 \sqrt{3}}$

B. $|z| = \sqrt{5 - \sqrt{3}}$

C. $|z| = \sqrt{5 + 2 \sqrt{3}}$

D. $|z| = \sqrt{4 - 2 \sqrt{3}}$

Xem đáp án

Câu 32:

Cho hàm số $f (x) = e^{x} lnx$ . Khẳng định nào sau đây là đúng?

A. Hàm số có tập xác định là $D = ℝ$

B. Hàm số luôn nghịch biến trên $ℝ$

C. $\lim_{x \to 0^{+}} f (x) = - \infty$

D. Hàm số có duy nhất một điểm cực trị

Xem đáp án

Đáp án C

Câu 33:

Cho (H) là hình phẳng giới hạn bởi các đường $y = e^{x}$ , trục tung, trục hoành và đường thẳng x = 1. Gọi V là thể tích khối tròn xoay tạo thành khi quay hình (H) quanh trục Ox. Khẳng định nào sau đây là đúng về thể tích V?

A. $V = \frac{π}{2} e^{2}$

B. $V = \frac{π}{2} (e - 1)$

C. $V = \frac{1}{2} (e^{2} - 1)$

D. $V = \frac{π}{2} (e^{2} - 1)$

Xem đáp án

Câu 34:

Hàm số $y = - \frac{3}{4} x^{4} - 3 x^{2} + 1$ đồng biến trên các khoảng

A. $ℝ$

B. $(- \sqrt{2}; \sqrt{2})$

C. $(- \infty; 0)$

D. $(0; + \infty)$

Xem đáp án

Câu 35:

Biết rằng phương trình $3^{x} {.5}^{\frac{1}{2 x - 1}} = 15$ có hai nghiệm thực phân biệt $x_{1}, x_{2}$ . Tính $x_{1} x_{2}$ .

A. $x_{1} x_{2} = \log_{3} 5 + \frac{1}{2}$

B. $x_{1} x_{2} = - (\log_{3} 5 + \frac{1}{2})$

C. $x_{1} x_{2} = \log_{5} 3 + \frac{1}{2}$

D. $x_{1} x_{2} = - \log_{3} 5 + \frac{1}{2}$

Xem đáp án

Câu 36:

Trong các khốp chóp sau, khối chóp nào không có mặt cầu ngoại tiếp?

A. Hình chóp có đáy là hình chữ nhật

B. Hình chóp có đáy là hình bình hành

C. Hình chóp có đáy là hình vuông

D. Hình chóp tam giác

Xem đáp án

Đáp án B

Hình chóp có đáy là hình bình hành

Câu 37:

Tổng hai nghiệm dương liên tiếp nhỏ nhất của phương trình $\cos 4 x + \frac{1}{2} = 0$ là

A. $\frac{π}{2}$

B. $\frac{7 π}{6}$

C. $\frac{π}{6}$

D. $\frac{5 π}{6}$

Xem đáp án

Câu 38:

Cho hình lăng trụ đứng ABC.A′B′C′ có đáy là tam giác đều cạnh a. Cạnh bên BB′=b. Thể tích của khối lăng trụ ABC.A′B′C′ là

A. $a^{3} b \sqrt{3}$

B. $\frac{a^{2} b \sqrt{3}}{4}$

C. $a^{2} b \sqrt{3}$

D. $\frac{a^{3} b \sqrt{3}}{3}$

Xem đáp án

Đáp án B

Câu 39:

Tìm các giá trị thực của a để hàm số $y = \log_{a + 1} x$ đồng biến trên (0;+∞).

A. a > 1

B. a > 2

C. a > 0

D. a > -1

Xem đáp án

Câu 40:

Một người thợ thiết kế một bể các hình hộp chữ nhật có đáy nhưng không có nắp đậy, có chiều cao là 75cm, thể tích bể là $600000 {cm}^{3}$ . Người thợ dùng loại kính để sử dụng làm mặt bên có giá thành 700000 đồng/ $m^{2}$ và loại kính để làm mặt đáy có giá thành 1000000 đồng/ $m^{2}$ . Giả sử phần tiếp xúc giữa các mặt bên là không đáng kể. Số tiền mua kính ít nhất để hoàn thành bể cá là

A. 2,678 (triệu đồng)

B. 3,012 (triệu đồng)

C. 2,132 (triệu đồng)

D. 2,108 (triệu đồng)

Xem đáp án

Câu 41:

Cho cấp số cộng $(u_{n})$ có công sai $d = - 3$ và $u_{2}^{2} + u_{3}^{2} + u_{4}^{2}$ đạt giá trị nhỏ nhất. Tính tổng $S_{100}$ của 100 số hạng đầu tiên của cấp số cộng đó.

A. $S_{100} = - 14650$

B. $S_{100} = - 14400$

C. $S_{100} = - 15450$

D. $S_{100} = - 14250$

Xem đáp án

Câu 42:

Cho đa giác đều $A_{1} A_{2} . .. A_{2 n}$ $(n \geq 2, n \in Z)$ nội tiếp đường tròn O. Biết rằng số tam giác trong 2n điểm $A_{1}, A_{2}, . .., A_{2 n}$ gấp 20 lần số hình chữ nhật có 4 đỉnh trong 2n điểm đó. Tìm n.

A. 12

B. 8

C. 16

D. 10

Xem đáp án

Câu 43:

Cho hình chóp đều S.ABCD có khoảng cách từ A đến mặt phẳng (SCD) bằng a. Tính giá trị nhỏ nhất của thể tích khối chóp S.ABCD theo a.

A. $\frac{a^{3} \sqrt{3}}{6}$

B. $\frac{a^{3} \sqrt{3}}{2}$

C. $\frac{a^{3} \sqrt{3}}{4}$

D. $\frac{a^{3} \sqrt{3}}{3}$

Xem đáp án

Câu 44:

Cho hình chóp S ABCD, có đáy ABCD là hình vuông cạnh bằng 1. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy (ABCD). Tính khoảng cách từ A đến (SCD).

A. $\frac{\sqrt{21}}{7}$

B. $\sqrt{2}$

C. 1

D. $\frac{2 \sqrt{3}}{3}$

Xem đáp án

Câu 45:

Tìm số nghiệm của phương trình $\sin (cosx) = 0$ trên đoạn x∈[0;2π].

A. 0

B. 1

C. 2

D. Vô số

Xem đáp án

Câu 46:

Cho tứ diện SABC có tam giác ABC vuông tại B, $AB = a, BC = a \sqrt{3}$ và $SA = a \sqrt{2}$ , $SB = a \sqrt{2}, SC = a \sqrt{5}$ . Tính bán kính mặt cầu ngoại tiếp tứ diện S.ABC.

A. $R = \frac{a \sqrt{37}}{28}$

B. $R = \frac{a \sqrt{259}}{7}$

C. $R = \frac{a \sqrt{259}}{14}$

D. $R = \frac{a \sqrt{37}}{14}$

Xem đáp án

Câu 47:

Cho hình lập phương ABCD.A’B’C’D’. Gọi M là trung điểm của DD’ (tham khảo hình vẽ dưới đây). Tính cosin của góc giữa hai đường thẳng B’C và C’M.

A. $\frac{1}{3}$

B. $\frac{1}{\sqrt{10}}$

C. $\frac{1}{\sqrt{3}}$

D. $\frac{2 \sqrt{2}}{9}$

Xem đáp án

Câu 48:

Trong các số phức z thỏa mãn $|z - 2 - 3 i| = 2$ , gọi $z_{0}$ là số phức có môđun nhỏ nhất. Khi đó $|z_{0}|$ bằng

A. $|z_{0}| = \sqrt{15 - 4 \sqrt{13}}$

B. $|z_{0}| = \sqrt{18 - 4 \sqrt{13}}$

C. $|z_{0}| = 2 \sqrt{4 - \sqrt{13}}$

D. $|z_{0}| = \sqrt{17 - 4 \sqrt{13}}$

Xem đáp án

Câu 49:

Cho hàm số $f (x) = \{\begin{cases} \frac{\sqrt{2 x + 1} - 1}{x} khi x \neq 0 \\ m^{2} + 2 m + 1 khi x = 0 \end{cases}$ . Tìm tất cả các giá trị của tham số m để hàm số liên tục tại x=0.