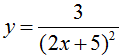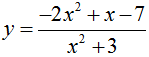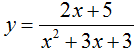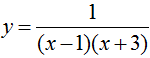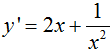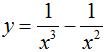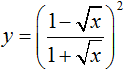Trắc nghiệm Toán 11 Chương 5: Đạo hàm cơ bản (phần 2) (có đáp án)
-
2879 lượt thi
-
25 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 2:
Tính đạo hàm của hàm số sau: y = (x7 + x)2.
Xem đáp án
Chọn D.
Sử dụng công thức đạo hàm của hàm hợp 
(với u = x7 + x )
y' = 2(x7 + x).(x7 + x)’ = 2(x7 + x)(7x6 + 1)
Câu 3:
Tính đạo hàm của hàm số sau: y = (2x3 – 3x2 – 6x + 1)2.
Xem đáp án
Chọn D.
Sử dụng công thức đạo hàm của hàm hợp 
với u = 2x3 – 6x + 1
y' = 2(2x3 – 3x2 - 6x + 1)(2x3 – 3x2 - 6x + 1)’ = 2(2x3 – 3x2 - 6x + 1)(6x2 – 6x - 6).
Câu 4:
Tính đạo hàm của hàm số sau: y = (1 – 2x2)3.
Xem đáp án
Chọn B.
Sử dụng công thức đạo hàm hàm hợp 
với u = 1 – 2x2
y' = 3(1 – 2x2)2(1 – 2x2)’ = 3(1 – 2x2)2(-4x) = -12x(1 – 2x2)2.
Xét hai câu sau:
Câu 10:
Đạo hàm của hàm số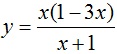 
bằng biểu thức nào sau đây?
Xem đáp án
Chọn B.
Áp dụng công thức 
.Có : 
, nên:
.
Câu 21:
Cho hàm số y = x3 – 3x2 – 9x – 5. Phương trình y’ = 0 có nghiệm là:
Xem đáp án
Chọn B.
Ta có : y’ = 3x2 – 6x – 9
y' = 0 ⇔ 3x2 – 6x – 9 = 0 ⇔ x = -1; x = 3.
Câu 24:
Cho hàm số y = -4x3 + 4x. Để y’ ≥ 0 thì x nhận các giá trị thuộc tập nào sau đây
Xem đáp án
Chọn B.
Ta có y = -4x3 + 4x ⇒ y’ = -12x2 + 4.
Nên 
