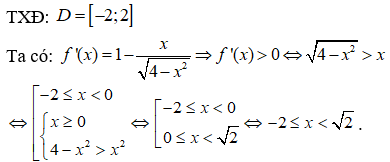20 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 11 Chương 5: Đạo hàm nâng cao (phần 2) (có đáp án)

Câu 1:

Tìm các giá trị x thoả mãn f’(x) > 0 với $f (x) = x + \sqrt{4 - x^{2}}$

A. $- 2 \leq x \leq \sqrt{2}$

B. $x \leq \sqrt{2}$

C. -2 ≤ x

D. x < 0

Xem đáp án

Chọn A.

Câu 2:

Tìm m để các hàm số y = (m – 1)x³ – 3(m + 2)x² – 6(m + 2)x + 1 có y’ ≥ 0, ∀ x ∈ R.

A. m ≥ 3

B. m ≥ 1

C. m ≥ 4

D. $m \geq 4 \sqrt{2}$

Xem đáp án

Chọn C.

Câu 3:

Tìm m để các hàm số $y = \frac{m x^{3}}{3} - m x^{2} + (3 m - 1) x + 1$ có y’ ≤ 0, ∀x ∈ R

A. $m \leq \sqrt{2}$

B. m ≤ 2

C. m ≤ 0

D. m < 0

Xem đáp án

Chọn C.

Câu 4:

Cho hàm số y = x³ + 3x² – 9x + 5 (C). Trong tất cả các tiếp tuyến của đồ thị (C), hãy tìm tiếp tuyến có hệ số góc nhỏ nhất.

A: y = -2x + 4

B: x + y + 12 = 0

C: 12x + y – 4 = 0

D: x - 12y + 4 = 0

Xem đáp án

Chọn C.

Ta có y’ = f’(x) = 3x² + 6x – 9

Gọi x_o là hoành độ tiếp điểm của tiếp tuyến, vậy f’(x_o) = 3x₀² + 6x_o – 9

Ta có 3x₀² + 6x_o – 9 = 3(x_o² + 2x_o + 1) – 12 = 3(x_o + 1)² – 12 ≥ -12, ∀x_o ∈ (C)

Vậy mìn’(x₀) = -12 tại x_o = -1 ⇒ y_o = 16

Suy ra phương trình tiếp tuyến cần tìm: y = -12(x + 1) + 16 hay y = -12x + 4.

Câu 5:

Cho hàm số $y = \frac{x + 2}{2 x + 3} (1)$ . Viết phương trình tiếp tuyến của đồ thị hàm số (1), biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác OAB cân tại gốc tọa độ 0.

A: x + y = 0

B: x + y + 2 = 0

C: x + y – 2 = 0

D: Cả A và C đúng

Xem đáp án

Chọn B.

Câu 6:

Cho hàm số y = x³ + 3mx² + (m + 1)x + 1 (1), m là tham số thực. Tìm các giá trị của m để tiếp tuyến của đồ thị của hàm số (1) tại điểm có hoành độ x = -1 đi qua điểm A(1; 2).

A: 1

B: -1

C: 3/4

D: 5/8

Xem đáp án

Chọn D.

Câu 7:

Cho hàm số $y = \frac{3 x + 1}{x + 1} (1)$ . Diện tích của tam giác tạo bởi các trục tọa độ và tiếp tuyến của đồ thị của hàm số (1) tại điểm M(-2; 5) là a/b ( phân số tối giản) .Tính a + b.

A: 81

B: 4

C: 85

D: đáp án khác

Xem đáp án

Chọn C.

Câu 8:

Cho hàm số $y = \sqrt{3} x^{3} + 4 (C)$ . Có mấy phương trình tiếp tuyến của đồ thị biết tiếp tuyến tạo với đường thẳng $(d) : - x + \sqrt{3} y + 6 = 0$ góc $30^{°}$

A: 1

B: 2

C: 3

D: 4

Xem đáp án

Chọn C.

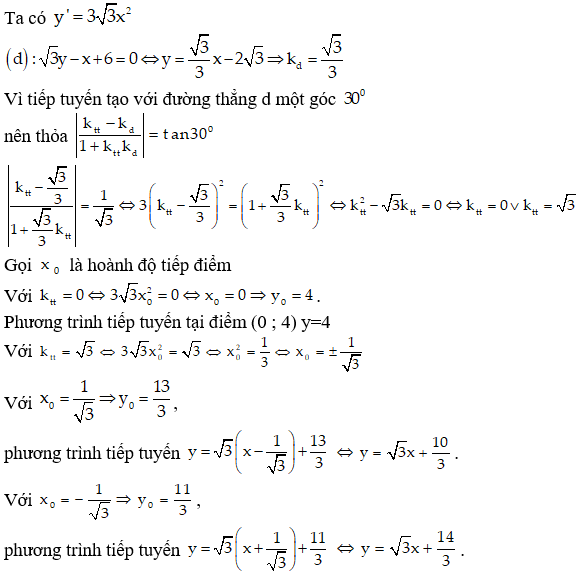
Câu 9:

Cho hàm số y = -x³ – 3x² + 9x – 5 (C). Trong tất cả các tiếp tuyến của đồ thị (C), hãy tìm tiếp tuyến có hệ số góc lớn nhất.

A: y = 8x - 3

B: y = 6x - 4

C: y = 10x - 2

D: y = 12x - 4

Xem đáp án

Chọn D.

Ta có y’ = -3x² – 6x + 9

Gọi x_o là hoành độ tiếp điểm của tiếp tuyến, ta có f’(x_o) = -3x_o² – 6x_o + 9

⇔ f’(x_o) = -3(x_o² + 2x_o + 1) + 12 = -3(x_o + 1)² + 12 ≤ 12

Từ đó suy ra maxf’(x_o) = 12 tại x_o = -1.

Với x_o = -1 ⇒ y_o = -16, phương trình tiếp tuyến cần tìm: y = 12x - 4.

Câu 10:

Cho hàm số $y = \frac{2 x - 1}{x - 1}$ . Gọi I(1; 2) Tìm điểm M ∈ (C) sao cho tiếp tuyến của (C) tại M vuông góc với đường thẳng IM?

A: M(3; 2; 5)

B: (0; 1)

C: (2; 3)

D: Cả B và C đúng

Xem đáp án

Chọn D.

Câu 11:

Cho hàm số $y = \frac{2 x}{x + 1} (C)$ . Có mấy điểm M ∈ (C), biết tiếp tuyến của (C) tại M cắt hai trục tọa độ tại A; B và tam giác OAB có diện tích bằng 1/4.

A: 0

B: 1

C: 2

D: 3

Xem đáp án

Chọn C.

Câu 12:

Cho đồ thị $(C_{m}) : y = \frac{(3 m + 1) x - m}{x + m}$ . Tìm m để tiếp tuyến tại giao điểm của (C_m) với Ox song song với đường thẳng d: y = -x - 5.

A: -1/6 ; -1/2

B: -1/4

C: -1/2 ; 1

D: Tất cả sai

Xem đáp án

Chọn A.

Câu 13:

Cho hàm số (C): $y = \frac{x + 2}{x - 2}$ . Viết phương trình tiếp tuyến đi qua A(-6; 5) của đồ thị (C).

A: y = x + 1

B: y = -x - 1

C: y = -x + 1

D: Đáp án khác

Xem đáp án

Chọn D.

Câu 14:

Gọi (C_m) là đồ thị của hàm số $y = \frac{1}{3} x^{2} - \frac{m}{2} x^{2} + \frac{1}{3} (*)$ (m là tham số).

Gọi M là điểm thuộc (C_m) có hoành độ bằng -1. Tìm m để tiếp tuyến của (C_m) tại điểm M song song với đường thẳng 5x – y = 0

A: m = 1

B: m = 2

C: m = 3

D: m = 4

Xem đáp án

Chọn D.

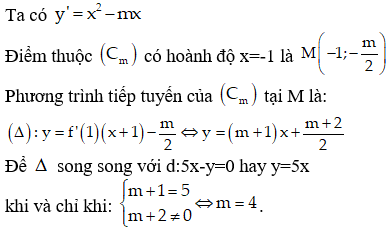
Câu 15:

Có mấy điểm $M \in (C) : y = \frac{x - 1}{2 x + 2}$ sao cho tiếp tuyến với (C) tại M tạo với hai trục tọa độ một tam giác có trọng tâm nằm trên đường thẳng d: 4x + y = 0 ?Có mấy điểm sao cho tiếp tuyến với (C) tại M tạo với hai trục tọa độ một tam giác có trọng tâm nằm trên đường thẳng d: 4x + y = 0 ?

A: không có

B: 1

C: 2

D: 3

Xem đáp án

Chọn C.

Câu 16:

Tìm A ∈ (C): y = x³ – 3x + 1 biết rằng tiếp tuyến của đồ thị (C) tại điểm A cắt đồ thị (C) tại B (khác điểm A) thỏa: x_A + x_B = 1?

A: (0; 1)

B: (-1; 3)

C: (2; 3)

D: Đáp án khác

Xem đáp án

Chọn B.

Câu 17:

Cho hàm số $y = \frac{x + 1}{x - 1}$ (C). Có bao nhiêu cặp điểm A, B thuộc (C) mà tiếp tuyến tại đó song song với nhau:

A. 0.

B. 2.

C. 1.

D. Vô số.

Xem đáp án

Chọn D.

Câu 18:

Cho hàm số $y = \frac{2 x - 3}{1 - x}$ .Viết phương trình tiếp tuyến với đồ thị hàm số biết tiếp tuyến vuông góc với đường thẳng d : x – y + 2017 = 0.

A: y = -x + 3

B: y + x = 1

C: x + y + 3 = 0; x + y – 1 = 0

D: Đáp án khác

Xem đáp án

Chọn C.

Câu 19:

Cho hàm số $y = \frac{3 x - 2}{x - 2}$ .Viết phương trình tiếp tuyến d với đồ thị hàm số biết d tạo với trục hoành một góc α mà $\cos α = \frac{1}{\sqrt{17}}$

A. 4x+y-3=0; 4x+y-19=0

B. 4x+y+3=0; 4x+y+19=0

C. 4x-y-3=0; 4x-y+19=0

D: Đáp án khác

Xem đáp án

Chọn A.

Câu 20:

Cho hàm số y = x³ – 3x² + 1 (C). Tìm tổng hoành độ của hai điểm A; B trên đồ thị hàm số sao cho tiếp tuyến của đồ thị (C) tại A; B song song với nhau và $A B = 4 \sqrt{2}$

A: 1

B: 2

C: 3

D: 5

Xem đáp án

Chọn B.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Toán 11 Ôn tập chương 5: Đạo hàm (có đáp án)

Trắc nghiệm Toán 11 Chương 5: Đạo hàm nâng cao (phần 2) (có đáp án)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương