Trắc nghiệm Toán 11 Chương 5: Đạo hàm cơ bản (phần 5) (có đáp án)
-
3806 lượt thi
-
24 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Tính đạo hàm cấp hai của các hàm số sau: y = xcos2x
Xem đáp án
Chọn C.
y' = cos2x – 2xsin2x;
y” = -2sin2x – (2sin2x + 4xcos2x) = -4sin2x – 4xcos2x.
Câu 2:
Cho hàm số y = f(x) = (x – 1)2. Biểu thức nào sau đây chỉ vi phân của hàm số f(x)?
Xem đáp án
Chọn A.
Ta có dy = f’(x)dx = 2(x – 1)dx.
Câu 3:
Tìm vi phân của các hàm số y = x3 + 2x2
Xem đáp án
Chọn D.
Ta có :
y’ = 3x2 + 4x
dy = (3x2 + 4x)dx
Câu 5:
Cho hàm số y = x3 – 9x2 + 12x - 5. Vi phân của hàm số là:
Xem đáp án
Chọn A.
Ta có
dy = (x3 – 9x2 + 12x – 5)’dx = (3x2 – 18x + 12)dx.
Câu 6:
Tìm vi phân của các hàm số y = (3x + 1)10
Xem đáp án
Chọn D.
Ta có
Vi phân của hàm số đã cho là:
dy = 30(3x + 1)9dx.
Câu 7:
Tìm vi phân của các hàm số y = sin2x + sin3x
Xem đáp án
Chọn B.
y’= 2cos2x + 3sin2x.cosx
dy = (2cos2x + 3sin2xcosx)dx.
Câu 8:
Tìm vi phân của các hàm số y = tan2x
Xem đáp án
Chọn D.
Ta có :
y’ = 2(1 + tan22x)
dy = 2(1 + tan22x)dx.
Câu 10:
Cho hàm số y = x3 – 5x + 6 . Vi phân của hàm số là:
Xem đáp án
Chọn A.
Ta có dy = (x3 – 5x + 6)’dx = (3x2 – 5)dx.
Câu 14:
Cho hàm số y = sinx – 3cosx. Vi phân của hàm số là:
Xem đáp án
Chọn C.
Ta có dy = (sinx – 3cosx)’dx = (cosx + 3sinx)dx.
Câu 15:
Cho hàm số y = sin2x. Vi phân của hàm số là:
Xem đáp án
Chọn B.
Ta có dy = d(sin2x) = (sin2x)’dx = cosx.2sinxdx = sin2xdx.
Câu 18:
Tìm vi phân của hàm số y = (x3 – 2x2)2.
Xem đáp án
Chọn B.
Ta có : dy = ((x3 – 2x2)2)’.dx = (2(x3 – 2x2)’(x3 – 2x2))dx = 2(3x2 – 4x)(x3 – 2x2)dx
= (6x5 – 20x4 + 16x3)dx.
tại điểm x = 1 ứng với 
Câu 20:
Vi phân của hàm số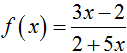 
tại điểm x = -1 ứng với Δx = 0,01 xấp xỉ bằng
Xem đáp án
Chọn B.
Ta có:
Nên 
Câu 21:
Vi phân của hàm số f(x) = sin(3x – 2) + cos(x2 + 1) tại điểm x = 0 ứng với Δx = 0,5 xấp xỉ bằng:
Xem đáp án
Chọn B.
Ta có:
f’(x) = 3cos(3x – 2) – 2x.sin(x2 + 1)
Nên df(xo) = f’(xo). Δx = [3cos(3.0 – 2) – 2.0.sin(0 + 1)].0,5 ≈ -0,624
Câu 22:
Tìm vi phân của hàm số f(x) = tan2x – sin2(x + 1) tại điểm x = -1 ứng với Δx = -0,02 xấp xỉ bằng:
Xem đáp án
Chọn D.
Ta có
Câu 23:
Một chất điểm chuyển động thẳng được xác định bởi phương trình s(t) = t3 + 5t2 + 5, trong đó t tính bằng giây và s tính bằng mét. Tính gia tốc của chuyển động khi t = 2.
Xem đáp án
Chọn A
Ta có s’(t) = 3t2 + 10t ; s”(t) = 6t + 10
Do đó gia tốc chuyển động có phương trình a(t) = 6t + 10
Gia tốc của chuyển động tại t = 2 là : a(2) = 6.2 + 10 = 22
Câu 24:
Một chất điểm chuyển động thẳng xác định bởi phương trình s(t) = 2t3 – 2t2 + 6 trong đó t là giây ; s là mét. Tính vận tốc của chuyển động khi t = 1
Xem đáp án
Chọn B.
Ta có: s’(t) = 6t2 – 4t
Nên phương trình vận tốc của chuyển động là: v(t) = 6t2 – 4t (m/s)
Vận tốc của vật khi t = 1 là: v(1) = 6.1 - 4.1 = 2(m/s)