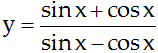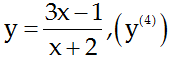Trắc nghiệm Toán 11 Chương 5: Đạo hàm cơ bản (phần 4) (có đáp án)
-
2882 lượt thi
-
25 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho đường cong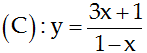 
. Viết phương trình tiếp tuyến của (C) biết tiếp tuyến song song với đường thẳng
(d): x - 4y – 21 = 0.
Xem đáp án
Chọn C
Tập xác định D = R \ {1}. Ta có 
Có 
Vì tiếp tuyến song song với d nên ktt = kd = 1/4.
Gọi M(xo; yo) là tọa độ tiếp điểm của tiếp tuyến, ta có f’(x0) = ktt 
⇔ (1- xo )2 = 16 ⇔ xo = 5 ∨ xo = -3
Với xo = 5 ⇒ yo = -4, phương trình tiếp tuyến tại điểm này là:
(loại, vì trùng với d).
Với xo = -3 ⇒ yo = -2, phương trình tiếp tuyến tại điểm này là:
Hay 4y = x - 5 x - 4y - 5 =0
Câu 2:
Cho đường cong 
Số tiếp tuyến của (C) biết tiếp tuyến vuông góc với đường thẳng (Δ): 2x + 2y – 9 = 0.
Xem đáp án
Chọn B
Tập xác định D = R \ {1}. Ta có 
Vì tiếp tuyến vuông góc với Δ nên, 
Gọi N(xo; yo) là tọa độ tiếp điểm của tiếp tuyến, ta có f’(xo) = ktt 
⇔ (1- xo )2 = 4 ⇔ xo = 3 ∨ xo = -1.
Với xo = 3 ⇒ y = -5, phương trình tiếp tuyến tại điểm này là:
⇔ y = 1(x – 3) – 5 ⇔ y = x – 8
Với xo = -1 ⇒ y = -1, phương trình tiếp tuyến tại điểm này là:
⇔ y = 1(x + 1) – 1 ⇔ y = x
Câu 3:
Cho hàm số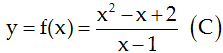 
.Viết phương trình tiếp tuyến của (C) tại điểm M(2; 4).
Xem đáp án
Chọn A.
Ta có: 
Ta có xo = 2 ⇒ f’(xo) = f’(2) = -1
Phương trình tiếp tuyến của (C) tại điểm M(2; 4) là
y = -1(x - 2) + 4 hay y = -x + 6.
Câu 4:
Cho hàm số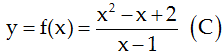
.
Viết phương trình tiếp tuyến của (C) biết tiếp tuyến có hệ số góc k = 1.
Xem đáp án
Chọn D.
Ta có: 
Gọi xo là hoành độ tiếp điểm của tiếp tuyến với đồ thị, ta có f’(xo) = 1
(vô lý).
Kết luận không có tiếp tuyến nào có hệ số góc bằng 1.
Câu 5:
Cho hàm số (C):
. Tìm phương trình tiếp tuyến với (C). Tại điểm có hoành độ xo = 1/2.
Xem đáp án
Chọn A.
Ta có 
Với 
Vậy phương trình tiếp tuyến tại điểm 
là y = -2(x - 1/2) + 1/2
Hay y = -2x + 3/2.
Câu 7:
Tính đạo hàm của hàm số sau: y = cos2x
Xem đáp án
Chọn B.
Áp dụng công thức 
với u = cos x.
y’ = (cos2x)’ = 2.cosx. (cosx)’ = 2cosx.(-sinx) = -sin2x.
Câu 12:
Giải phương trình y’ = 0 trong trường hợp sau: y = sin2x – 2cosx.
Xem đáp án
Chọn D.
Trước tiên, ta có: y’ = 2cos2x + 2sinx.
Khi đó, phương trình có dạng:
2cos2x + 2sinx = 0 
Câu 14:
Hàm số có đạo hàm là:
Xem đáp án
Chọn A.
Ta có
y’ = (sin2x)’.cosx + sin2x.(cosx)’ = 2cos2xsinx – sin3x
= sinx(2cos2x – sin2x) = sinx(3cos2x – 1).
Câu 15:
Hàm số y = x2.cosx có đạo hàm là:
Xem đáp án
Chọn A.
y' = (x2)’.cosx + x2(cosx)’ = 2x.cosx – x2.sinx.
Câu 16:
Cho hàm số y = cos3x.sin2x. Tính 
bằng:
Xem đáp án
Chọn B.
y' = (cos3x)’sin2x + cos3x(sin2x)’ = -3sin3x.sin2x + 2cos3x.cos2x.
. Chọn đáp án sai:
Giá trị 
bằng:
Câu 19:
Cho hàm số y = cos2x + sinx. Phương trình y’ = 0 có bao nhiêu nghiệm thuộc khoảng (0; π)
Xem đáp án
Chọn C.
y' = -2cosxsinx + cosx = cosx(1 – 2sinx)
Vì 
. Vậy có 3 nghiệm thuộc khoảng (0; π).
Câu 20:
Tính đạo hàm cấp ba của hàm số sau: y = xsin2x
Xem đáp án
Chọn D.
Có y’ = x’sin2x + x.(sin2x)’ = sin2x + 2xcos2x
⇒ y’’ = (sin2x)’ + (2x)’cos2x + 2x(cos2x)’
= 2 cos2x +2. cos2x + 2x. (- 2sin 2x )
= 4cos2x – 4xsin2x
⇒ y’’’ = 4(cos2x)’ – (4x)’sin2x – 4x(sin2x)’ = -8sin2x – 4sin2x – 8xcos2x
= -12sin2x – 8xcos2x.
Câu 21:
Tính đạo hàm đến cấp đã chỉ ra của hàm số sau: y = cos2x,(y’’’)
Xem đáp án
Ta có 
⇒ y’’ = -2cos2x ⇒ y’’’ = 4sin2x.
Câu 22:
Tính đạo hàm đến cấp đã chỉ ra của hàm số sau: y = x4 – sin2x, (y(4))
Xem đáp án
Chọn C.
y = x4 - sin2x
⇒ y’ = 4x3 – 2cos2x ⇒ y’’ = 12x2 + 4sin2x
⇒ y’’’ = 24x + 8cos2x ⇒ y(4) = 24 – 16sin2x
Câu 24:
Cho f(x) = (2x – 3)5. Khi đó f”(3) và f”’(3) lần lượt là:
Xem đáp án
Chọn A.
f’(x) = 5(2x – 3)4(2x – 3)’ = 10(2x – 3)4
f”(x) = 40(2x – 3)3(2x – 3)’ = 80(2x – 3)3
f”’(x) = 240(2x – 3)2(2x – 3)’ = 480(2x – 3)2
Vậy: f”(3) = 80(2.3 – 3)3 = 2160
f”’(3) = 480(2.3 – 3)2 = 4320
Câu 25:
Tính đạo hàm cấp hai của các hàm số sau: y = x2sinx
Xem đáp án
Chọn C.
y' = 2x.sinx + x2cosx
y” = 2sinx + 2xcosx + 2xcosx + x2(-sinx) = 2sinx + 4xcosx – x2sinx.