Các đại lượng đặc trưng của sóng cơ
-
575 lượt thi
-
17 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Trả lời:
Sóng dọc: là sóng trong đó các phần tử của môi trường dao động theo phương trùng với phương truyền sóng.
Sóng ngang: là sóng trong đó các phần tử của môi trường dao động theo phương vuông góc với phương truyền sóng.
=>Để phân biệt sóng ngang hay sóng dọc người ta dựa vào phương dao động và phương truyền sóng.
Đáp án cần chọn là: D
Câu 2:
 Xem đáp án
Xem đáp án
Trả lời:
A, B, C - đúng
D - sai vì: Khi sóng truyền qua, các phần tử của môi trường chỉ dao động quanh vị trí cân bằng của chúng mà không chuyển dời theo sóng, chỉ có pha dao động của chúng được truyền đi.
Đáp án cần chọn là: D
Câu 3:
 Xem đáp án
Xem đáp án
Trả lời:
Tốc độ truyền sóng v : là tốc độ lan truyền dao động trong môi trường
Phụ thuộc vào bản chất của môi trường truyền (tính đàn hồi và mật độ môi trường): vR>vL>vK
Đáp án cần chọn là: C
Câu 4:
 Xem đáp án
Xem đáp án
Trả lời:
Khi sóng cơ truyền càng xa nguồn thì biên độ và năng lượng sóng càng giảm
Đáp án cần chọn là: D
Câu 5:
 Xem đáp án
Xem đáp án
Trả lời:
B - sai vì: Năng lượng sóng luôn không đổi khi môi trường truyền sóng là 1 đường thẳng
Đáp án cần chọn là: B
Câu 6:
Một nguồn dao động đặt tại điểm O trên mặt chất lỏng nằm ngang phát ra dao động điều hòa theo phương thẳng đứng với phương trình uO = Acosωt. Sóng do nguồn dao động này tạo ra truyền trên mặt chất lỏng có bước sóng λ tới điểm M cách O một khoảng x. Coi biên độ sóng và vận tốc sóng không đổi khi truyền đi thì phương trình dao động tại điểm M là:
 Xem đáp án
Xem đáp án
Trả lời:
Phương trình sóng tại M cách O một khoảng x là:
\[{u_M} = A\cos \left( {t - \frac{x}{v}} \right) = A\cos \left( {\omega t - \frac{{2\pi x}}{\lambda }} \right)\]
Đáp án ần chọn là: D
Câu 7:
 Xem đáp án
Xem đáp án
Trả lời:
Ta có, khoảng cách giữa năm ngọn sóng liên tiếp là:
4λ = 20m = >λ = 5m
Đáp án cần chọn là: A
Câu 8:
Một người ngồi ở bờ biển đếm được 20 ngọn sóng đi qua trước mặt trong 76s. Chu kì dao động của nước biển là:
 Xem đáp án
Xem đáp án
Trả lời:
Ta có, 20 ngọn sóng đi qua trước mặt tương đương với 19 bước sóng hay 19 chu kì dao động
=> 19T = 76s =>T = 4s
Đáp án cần chọn là: D
Câu 9:
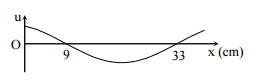
Một sóng hình sin truyền trên một sợi dây dài. Ở thời điểm t, hình dạng của một đoạn dây như hình vẽ. Các vị trí cân bằng của các phần tử trên dây cùng nằm trên trục Ox. Bước sóng của sóng này bằng:
 Xem đáp án
Xem đáp án
Trả lời:
Từ đồ thị, ta có:
\[\frac{\lambda }{2} = 33 - 9 = 24cm\]
→ λ = 48cm
Đáp án cần chọn là: A
Câu 10:
Một sóng ngang truyền trên sợi dây đàn hồi rất dài với tần số 500Hz. Người ta thấy hai điểm A, B trên sợi dây cách nhau 200cm dao động cùng pha và trên đoạn dây AB có hai điểm khác dao động ngược pha với A. Tốc độ truyền sóng trên dây là:
 Xem đáp án
Xem đáp án
Trả lời:
2 điểm A, B dao động cùng pha và trên AB có 2 điểm khác dao động ngược pha với A.
→ AB = 2λ = 200cm
→ λ = 100cm
Ta có tốc độ truyền sóng:
v = λf = 100.500 = 50000cm/s = 500m/s
Đáp án cần chọn là: C
Câu 11:
Một sợi dây đàn hồi rất dài có đầu A dao động với tần số f và theo phương vuông góc với sợi dây. Biên độ dao động là 4cm, vận tốc truyền sóng trên dây là 4(m/s). Xét một điểm M trên dây và cách A một đoạn 28cm, người ta thấy M luôn luôn dao động lệch pha với AA một góc \[\Delta \varphi = \left( {2k + 1} \right)\frac{\pi }{2}\]với k = 0, ±1, ±2, ..... Tính bước sóng λ? Biết tần số f có giá trị trong khoảng từ 22Hz đến 26Hz.
 Xem đáp án
Xem đáp án
Trả lời:
Độ lệch pha:
\[\Delta \varphi = \left( {2k + 1} \right)\frac{\pi }{2} = \frac{{2\pi d}}{\lambda }\]\[ \to f = \left( {2k + 1} \right)\frac{v}{{4d}}\]
Mặt khác: 22Hz < f < 26Hz
\[ \to 22 < f = \left( {2k + 1} \right)\frac{4}{{4d}} < 26\]
\[22 < \left( {2k + 1} \right)\frac{4}{{4.0,28}} < 26\]
→ 2,58 < k < 3,14
→ k = 3
\[ \to f = \left( {2.3 + 1} \right)\frac{4}{{4.0,28}} = 25Hz\]
\[ \to \lambda = \frac{v}{f} = \frac{4}{{25}} = 0,16m = 16cm\]
Đáp án cần chọn là: D
Câu 12:
Một sóng ngang có chu kì T = 0,2s truyền trong một môi trường đàn hồi có tốc độ 1m/s. Xét trên phương truyền sóng Ox, vào một thời điểm nào đó một điểm M nằm tại đỉnh sóng thì ở trước M theo chiều truyền sóng, cách M một khoảng từ 42cm đến 60cm có điểm N đang từ vị tri cân bằng đi lên đỉnh sóng . Khoảng cách MN là:
 Xem đáp án
Xem đáp án
Trả lời:
Bước sóng:
λ = vT = 1.0,2 = 0,2m
Độ lệch pha:
Khi điểm M ở đỉnh sóng, điểm N ở vị trí cân bằng đang đi lên
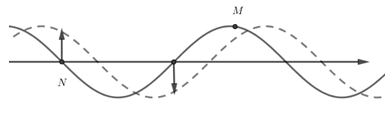
Theo hình vẽ thì khoảng cách MN
\[MN = \frac{3}{4}\lambda + k\lambda \] với k = 0; 1; 2; …
\[0,42 < MN = \frac{3}{4}\lambda + k\lambda < 0,60\]
\[ \to 1,35 < k < 2,25\]
\[ \to k = 2\]
\[ \to MN = \frac{3}{4}\lambda + 2\lambda = 0,55m = 55cm\]
Đáp án cần chọn là: B
Câu 13:
Một dây đàn hồi dài có đầu A dao động theo phương vuông góc với sợi dây. Tốc độ truyền sóng trên dây là 4m/s. Xét một điểm M trên dây và cách A một đoạn 40cm, người ta thấy M luôn luôn dao động lệch pha so với A một góc
Δφ = (k + 0,5)π với k là số nguyên. Tính tần số, biết tần số f có giá trị trong khoảng từ 8Hz đến 13Hz.
 Xem đáp án
Xem đáp án
Trả lời:
+ Độ lệch pha giữa M và A:
\[\Delta \varphi = \frac{{2\pi d}}{\lambda } = \frac{{2\pi d}}{{\frac{v}{f}}}\]
\[ \Rightarrow \frac{{2\pi df}}{v} = \left( {k + 0,5} \right)\pi \]
\[ \Rightarrow f = \left( {k + 0,5} \right)\frac{v}{{2d}}\]
\[ \Rightarrow f = 5\left( {k + 0,5} \right)Hz\]
Theo đầu bài:
8Hz < f < 13Hz
⇒ 8 < (k + 0,5).5 < 13
⇒ 1,1 < k < 2,1
⇒ k = 2
⇒ f = 12,5Hz
Đáp án cần chọn là: D
Câu 14:
Sóng cơ có tần số 80 Hz lan truyền trong một môi trường với vận tốc 4 m/s. Dao động của các phần tử vật chất tại hai điểm trên một phương truyền sóng cách nguồn sóng những đoạn lần lượt 31 cm và 33,5 cm, lệch pha nhau góc:
 Xem đáp án
Xem đáp án
Trả lời:
Bước sóng là:
\[\lambda = \frac{v}{f} = \frac{4}{{80}} = 0,05\left( m \right) = 5\left( {cm} \right)\]
Hai chất điểm cách nhau một đoạn:
d = d2 – d1 = 33,5 – 31 = 2,5(cm)
Độ lệch pha giữa hai chất điểm là:
\[\Delta \varphi = \frac{{2\pi d}}{\lambda } = \frac{{2\pi .2,5}}{5} = \pi \left( {rad} \right)\]
Đáp án cần chọn là: B
Câu 15:
Hai điểm M, N cùng nằm trên một hướng truyền sóng và cách nhau một phần ba bước sóng. Biên độ sóng không đổi trong quá trình truyền. Tại một thời điểm, khi li dộ dao động của phần tử tại M là 3cm thì li độ dao động của phần tử tại N là -3cm. Biên độ dao động sóng bằng
 Xem đáp án
Xem đáp án
Trả lời:
Độ lệch pha của hai phần tử
\[\Delta \varphi = \frac{{2\pi d}}{\lambda } = \frac{{2\pi \frac{\lambda }{3}}}{\lambda } = \frac{{2\pi }}{3}\]
Vẽ trên vòng tròn lượng giác, ta có:
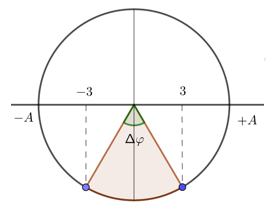
Từ vòng tròn lượng giác, ta có:
\[\sin \frac{{\Delta \varphi }}{2} = \frac{3}{A}\]
\[ \Rightarrow A = \frac{3}{{\sin \frac{{\Delta \varphi }}{2}}} = \frac{3}{{\sin \frac{\pi }{3}}} = 2\sqrt 3 cm\]
Đáp án cần chọn là: C
Câu 16:
Một sóng bề mặt ở nơi xảy ra động đất có thể coi một cách gần đúng là một sóng ngang hình sin. Giả sử tần số của sóng là f = 0,5 Hz thì biên độ sóng cần thiết bằng bao nhiêu để các vật đặt trên bề mặt đất bắt đầu rời khỏi mặt đất (lấy gia tốc trọng trường g = π2 = 10m/s2)
 Xem đáp án
Xem đáp án
Trả lời:
Tần số góc ω = 2πf = 2π.0,5 = π (rad/s)
Để các vật trên bề mặt đất bắt đầu rời khỏi mặt đất thì:
amax ≥ g
⇔ ω2A ≥ g
⇔ π2A ≥ π2
⇔ A ≥ 1,0(m)
Đáp án cần chọn là: A
Câu 17:
Trong thí nghiệm đo tốc độ truyền sóng trên sợi dây đàn hồi dài. Tần số máy phát là f = 10,0 ± 0,1Hz. Đo khoảng cách giữa 2 nút sóng liên tiếp cho kết quả:
d = 25 ± 1 cm. Vận tốc truyền sóng trên dây đàn hồi là:
 Xem đáp án
Xem đáp án
Trả lời:
Ta có: \[\frac{\lambda }{2}\]= 25 ± 1cm
⇒ λ = 50 ± 2 cm
⇒ λ = 0,5 ± 0,02 m
Lại có:
\[\overline v = \overline \lambda .\overline f = 0,5.10 = 5,0\,\left( {m/s} \right)\]
\[\frac{{\Delta v}}{v} = \frac{{\Delta \lambda }}{\lambda } + \frac{{\Delta f}}{f} = \frac{{0,02}}{{0,5}} + \frac{{0,1}}{{10}} = 0,05 = 5\% \]
Suy ra: v = 5,0m/s ± 5%
Đáp án cần chọn là: A
