Đề thi Đánh giá tư duy Đọc hiểu, Toán học có đáp án (Đề 2)
-
2439 lượt thi
-
62 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Thí sinh đọc bài 1 và trả lời câu hỏi từ 1 – 9:
Chụp ảnh bằng sóng siêu âm
Khi mang thai, đa số các phụ nữ đều đi chụp ảnh bằng siêu âm để xem tình trạng thai nhi, đặc biệt để kiểm tra các dị tật, sự phát triển của thai hay xác định giới tính. Tuy kết quả thu được là một tờ giấy có in ảnh rõ ràng, nhưng ít ai nói là chụp ảnh bằng siêu âm mà chỉ nói gọn là siêu âm, thí dụ hỏi: Siêu âm chưa? Siêu âm con trai hay con gái? Vậy siêu âm là gì và chụp ảnh bằng siêu âm dựa trên cơ chế gì?
Sóng âm là sự truyền dao động cơ trong môi trường khí, lỏng cũng như rắn. Sóng âm có tần số 20.000 Hz đến 109 Hz gọi là sóng siêu âm. Với tần sổ cao như vậy, người ta dễ tạo tia sóng siêu âm mảnh đi thẳng như một tia sáng. Tuy sóng siêu âm là sóng cơ (sóng đàn hồi), về bàn chất hoàn toàn khác với ánh sáng là sóng điện từ nhưng việc truyền tia siêu âm qua các môi trường có những nét giống như truyền tia sáng. Thí dụ về quang học, ta xét một tia sáng chiếu xuống một hồ nước. Khi đến mặt phân cách giừa không khí và nước, tia sáng bị phản xạ một phần, một phần bị khúc xạ. Nếu nước trong, ta có thể nhìn thấy đáy hồ. Đó là do ảnh sảng đến đáy hồ phản xạ lại đến mắt ta.
Nhìn vào cơ thể người bàng tia siêu âm cùng tương tự như nhìn vào cải hồ bằng tia sáng. Thật vậy, cơ thể người chứa nhiều nước và tia siêu âm rất dễ dàng đi vào môi trường như vậy không khác gì tia sáng chiểu vào hồ nước. Tốc độ siêu âm đi vào cơ thể cỡ 1.500 mét giây, nhưng tùy thuộc chất liệu chỗ nhiều nước, chỗ nhiều mỡ, chỗ nhiều thịt v.v. mà tốc độ đó thay đổi cỡ cộng trừ 60 mét/giây. Điều quan trọng là khi đi qua mặt phân cách giữa hai bộ phận của cơ thể do chất liệu khác nhau, nên tia siêu âm bị phản xạ không nhiều thì ít. Sau khi bị phản xạ ở mặt phân cách, tia siêu âm đi thẳng bị yếu đi, lại tiếp tục hành trình, nếu gặp mặt phân cách khác lại bị phản xạ, bị yếu đi và lại tiếp tục đi... Sau một số lần phản xạ như thế, đến một lúc tia siêu âm đi thẳng quá yếu, xem như bị tắt hẳn. Đối với cơ thể người, do cơ chế mồi lần phản xạ bị yếu đi như vậy nên tia siêu âm đi vào cơ thể chỉ vài chục centimet xem như bị tắt. Nhưng chính nhờ cơ chế bị phản xạ nhiều lần này mà mảy chụp ảnh siêu âm cỏ thể chụp được ảnh bên trong cơ thể đến độ sâu vài chục centimet.
Trong một máy chụp ảnh siêu âm. bộ phận quan trọng nhất là bộ phận đầu dò gồm bốn viên áp điện được đặt trên hình trụ quay được. Mỗi viên áp điện có thể phát ra các xung sóng siêu âm đồng thời thu được các xung sóng siêu âm phản xạ từ các mô, các bộ phận trong cơ thể. Trong mỗi giây đồng hồ. chu trình thu, phát lặp lại đến 400 lần. Quy trình chụp ánh của máy chụp ảnh siêu âm có thể phân ra ba giai đoạn như sau:
a, Phát ra sóng siêu âm: Máy phát ra xung điện dẫn đến viên áp điện. viên áp điện phát xung siêu âm với tần số nhất định.
b, Các mô phản xạ sóng siêu âm tạo ra tiếng vọng: Mỗi khi chùm siêu âm đi từ môi trường này sang môi trường kia, bị phản xạ (một phần) ở mặt phân cách. Khi viên áp điện nhận được tiếng vọng (sóng siêu âm phản xạ), viên áp điện biến siêu âm thành xung điện. Có thể gặp nhiều mặt phân cách có nhiều tiếng vọng. Máy phân tích thời gian giữa xung điện phát ra và các xung điện do phản xạ gây nên để từ đó tính các khoảng thời gian và các khoảng cách đến các mặt phản xạ.
c, Quét tia siêu âm để dựng ảnh: Các viên áp điện dịch chuyển theo nhịp độ quay của hình trụ gắn các viên áp điện. Máy căn cứ vào các số liệu về khoảng cách và tốc độ truyền siêu âm để dựng lên hình ảnh. Do những đặc điểm truyền và phản xạ sóng siêu âm, nên các máy chụp ảnh bằng siêu âm thường không phải là vạn năng mà là chuyên dụng (như máy chụp ảnh siêu âm dùng cho thai nhi. máy chụp ảnh siêu âm dùng để chụp gan. máy chụp ảnh siêu âm đo loãng xương, v.v.) Ưu điểm rất lớn của phép chụp ảnh bằng tia siêu âm là ít độc hại so với chụp ảnh tia X hay chụp ảnh bằng tia phóng xạ.
Ý chính của bài viết trên là gì?
 Xem đáp án
Xem đáp án
Chọn D
Phương pháp giải:
Dựa vào nội dung đoạn trích, kiến thức về câu chủ đề, phân tích.
Giải chi tiết:
Ý chính của bài viết là: Cơ chế tạo ảnh và nguyên lí hoạt động của máy chụp siêu âm.
Câu 2:
Trong đoạn 2 và đoạn 3, tác giả có ý gì khi nhắc đến sóng siêu âm và sóng ánh sáng?
 Xem đáp án
Xem đáp án
Chọn C
Phương pháp giải:
Căn cứ nội dung đoạn 2 và 3, phân tích.
Giải chi tiết:
Trong đoạn đã khẳng định: Tuy sóng siêu âm là sóng cơ sóng đàn hồi, về bản chất khác hoàn toàn với ánh sáng là sóng điện từ nhưng việc truyền tia siêu âm qua các môi trường có nét giống như truyền tia sáng.
=> Ý nghĩa khi nhắc đến là: Khẳng định sự giống nhau về cơ chế tạo ảnh của hai loại sóng này.
Câu 3:
Cụm từ “tốc độ đó” dùng để chỉ khái niệm nào dưới đây?
 Xem đáp án
Xem đáp án
Chọn D
Phương pháp giải:
Căn cứ nội dung đoạn 2 và 3, phân tích.
Giải chi tiết:
Trong đoạn đã khẳng định: Tuy sóng siêu âm là sóng cơ sóng đàn hồi, về bản chất khác hoàn toàn với ánh sáng là sóng điện từ nhưng việc truyền tia siêu âm qua các môi trường có nét giống như truyền tia sáng.
=> Ý nghĩa khi nhắc đến là: Khẳng định sự giống nhau về cơ chế tạo ảnh của hai loại sóng này.
Câu 4:
Theo đoạn 3, vì sao tia siêu âm bị tắt khi lan truyền vào cơ thể người?
 Xem đáp án
Xem đáp án
Chọn D
Phương pháp giải:
Căn cứ bài đọc hiểu, phân tích.
Giải chi tiết:
Khi đi qua mặt phân cách tia siêu âm sẽ bị phản xạ không nhiều thì ít, sau nhiều lần bị yếu đi và cuối cùng tắt hẳn.
=> Tia siêu âm bị tắt khi lan truyền vào cơ thể vì: phản xạ xảy ra liên tục tại các mặt phân cách giữa các bộ phận trong cơ thể.
Câu 5:
Câu nào sau đây KHÔNG phản ánh đúng nội dung của bài đọc?
 Xem đáp án
Xem đáp án
Chọn C
Phương pháp giải:
Căn cứ bài đọc hiểu, phân tích.
Giải chi tiết:
Câu không phản ánh nội dung bài đọc là: Sóng siêu âm và sóng ánh sáng có cùng bản chất là sóng điện từ.
Vì: Sóng siêu âm và sóng ánh sáng có bản chất khác nhau. Sóng siêu âm là sóng cơ sóng đàn hồi, sóng ánh sáng là sóng điện từ.
Câu 6:
Ý nào dưới đây thể hiệu đầy đủ vai trò của tấm áp điện trong đầu dò của máy siêu âm?
 Xem đáp án
Xem đáp án
Chọn C
Phương pháp giải:
Căn cứ bài đọc hiểu, phân tích.
Giải chi tiết:
Căn cứ vào đoạn: Mỗi viên áp điện có thể phát ra các xung sóng siêu âm đồng thời thu được các xung sóng siêu âm phản xạ từ các mô, các bộ phận trong cơ thể.
=> Câu thể hiện đầy đủ vai trò của tấm áp điện trong máy đầu dò là: Phát ra sóng siêu âm và thu sóng siêu âm phản xạ về.
Câu 7:
Bước nào sau đây KHÔNG được nêu trong quá trình các mô phản xạ sóng siêu âm tạo ra tiếng vọng?
 Xem đáp án
Xem đáp án
Chọn C
Phương pháp giải:
Căn cứ bài đọc hiểu, phân tích.
Giải chi tiết:
Bước không được nêu trong quá trình các mô phản xạ sóng siêu âm tạo ra tiếng vọng là: Thông số về tốc độ truyền siêu âm được sử dụng để dựng hình ảnh. Bước này được thể hiện ở: c. Quét tia siêu âm để dựng hình ảnh.
Câu 8:
Các ý trong “Quy trình ... lên hình ảnh” (phần 3 ý a, b, c) được sắp xếp theo trình tự nào?
 Xem đáp án
Xem đáp án
Chọn D
Phương pháp giải:
Căn cứ bài đọc hiểu, phân tích.
Giải chi tiết:
Trình tự được sắp xếp là theo thời gian.
Câu 9:
Ưu điểm của phương pháp chụp ảnh siêu âm được nhắc đến trong bài là gì?
 Xem đáp án
Xem đáp án
Phương pháp giải:
Căn cứ bài đọc hiểu, phân tích.
Giải chi tiết:
Dựa câu nội dung đoạn cuối: Ưu điểm rất lớn của phép chụp ảnh bằng tia siêu âm là ít độc hại so với chụp ảnh tia X hay chụp bằng tia phóng xạ.
=> Ưu điểm của phương pháp siêu âm là: Ít độc hại so với chụp ảnh bằng tia phóng xạ.
Câu 10:
Thí sinh đọc bài đọc và trả lời các câu hỏi từ 10 – 19
Trong một báo cáo về sự ấm lên của Bắc Cực, các nhà khoa học châu Âu đã kiểm tra dữ liệu về lịch sử nhiệt độ và phát hiện ra rằng nhiệt độ của Siberia - nơi nổi tiếng với nhiệt độ mùa đông lạnh nhất ờ Bắc bán cầu (nhiệt độ trung bình mùa đông khoảng -50°C) - đã ấm lên bất thường kể từ tháng 1/2020. Các nhà khoa học dự báo, đến năm 2050, hàng ngàn kilomet đường ống và đường giao thông, các tòa nhà, mỏ dầu và bể chứa, cảng hàng không, các cơ sở hạ tầng... trên khắp Bắc Cực sẽ bị ành hưởng nghiêm trọng khi mà gần 1/4 đất liền nơi đây nằm trên lớp băng vĩnh cửu. Thiệt hại có thể lên tới hàng trăm tỷ USD.
Nhiệt độ tăng khiến cháy rừng xảy ra thường xuyên hơn ớ Bẳc Cực. Tháng 8 năm ngoái, hơn 4 triệu ha rừng ở Siberia đã bốc cháy. Cháy rừng ở Bắc Cực cùng gây hậu quả rất lớn đối với khí hậu toàn cầu khi mà diện tích rừng nơi đây bao phủ 33% diện tích đất bề mặt trái đất và lưu trữ khoảng 50% lượng carbon trong lòng đất trên thế giới – nhiều hơn lượng carbon nằm trong tất cả sinh khối thực vật trên thế giới và tương đương với lượng carbon trong khí quyển.
Nhiệt độ cao, cháy rừng, băng vĩnh cửu tan sẽ giải phỏng khí carbon và metan đang bị lưu giữ. Chuyên gia về khi metan ở Bắc Cực - Katey Walter Anthony (Đại học Alaska, Mỹ) cho biết. "Khí carbon dioxide và metan thoát ra từ các địa điểm tan băng vĩnh cửu và các vụ cháy, chúng không chi tồn tại ở Bắc Cực mà sẽ hòa vào khí quyển và lưu thông trên toàn cầu, góp phần làm tăng nồng độ khí nhà kính". Theo Báo cáo Bắc Cực năm 2019 của Cơ quan Quản lý khí quyển và đại dương quốc gia Mỹ (NOAA), băng tan khắp Bắc Cực có thể sẽ thải ra khoảng 300-600 triệu tan carbon ròng mỗi năm vào bầu khí quyển Trái Đất. Kể từ khi có dữ liệu vệ tinh (năm 1979) đến nay, băng ở Bắc Cực vào mùa hè đã mất tới 40% diện tích và 70% khối lượng. Đây là một trong những dấu hiệu rõ ràng nhất về sự nóng lên toàn cầu.
Vùng cực của trái đất có nhiệt độ lạnh không chi vì nhận được ít ánh nắng mặt trời trực tiếp mà còn vì nơi đây có những khối băng trắng khổng lồ có tác dụng như tấm gương khổng lồ phản xạ hầu hết ánh sáng mặt trời trở lại không gian. Trong khi đó nước biển lại hấp thụ nhiệt từ ánh sáng mặt trời. Chính vì vậy, khi băng ở Bắc Cực tan chảy sẽ làm nước biển dâng, làm tăng diện tích bao phủ bời nước biển, tạo ra một vòng luẩn quẩn khiến nhiệt độ trái đất ngày càng ấm lên.
Băng Bắc Cực còn ảnh hường đến thời tiết trên toàn thế giới thông qua việc tác động tới dòng hải lưu. Đại dương và không khí hoạt động như động cơ nhiệt, vận chuyển nhiệt đến các cực một cách thường xuyên thông qua hoàn lưu khí quyển và dòng hải lưu đề tạo ra sự cân bằng. Diện tích băng biển giảm sẽ ảnh hưởng đến những quá trình này. Nhiệt độ vùng cực ấm lên phá vỡ lưu lượng nhiệt tổng thể của Trái Đất, trong khi hướng gió thay đổi đẩy nhiều băng hơn từ biển Bắc Cực về phía Đại Tây Dương. Tại đây, chúng sẽ tan thành nước lạnh và ngăn cản dòng hải lưu ấm lưu chuyển từ vùng nhiệt đới.
Sự nóng lên bất thường của Bắc Cực còn làm giảm chênh lệch nhiệt độ và áp suất giữa Bắc Cực và vĩ độ thấp -nơi cỏ nhiều người sinh sống. Điển hình như lãnh nguyên cùa làng Russkoye Ustye (Siberia), quần xã sinh vật lạnh nhất hành tinh, cũng đang bốc cháy. Các tòa nhà cũ của ngôi làng này đã chìm xuống sông trong 3 thập kỷ qua do sự xói mòn và tan băng vĩnh cửu gây ra. Trưởng làng, ông Portnyagin cho biết: "Đây là năm thứ 2 liên tiếp chúng tôi không có băng để di chuyển bằng xe trượt tuyết trong tháng 6. Trong khi đó, người dân làng không quen với nhiệt độ cao đã bị đau đầu và gặp các vấn đề về da. Những đàn cá cũng không còn thấy xuất hiện vì chúng lặn sâu xuống đáy biển. Các ngư dân đang vô cùng khốn khổ".
Trong khi người dân và các nhà khoa học đang rất lo lắng về những thay đổi bất thường và nhanh chóng của khí hậu Bắc Cực cũng như tương lai của khí hậu toàn cầu, thì các nhà chính trị lại dường như đang quan tâm hơn tới khía cạnh kinh tế và quyền kiểm soát Bắc Cực. Sở dĩ như vậy vì vùng cực này chứa đựng nguồn tài nguyên khổng lồ (30% trữ lượng khí đốt và 13% trữ lượng dầu mỏ của thế giới chưa được khai thác; nhiều mỏ kim loại hiếm dùng để chế tạo linh kiện điện tử và vũ khí). Khi băng tan, việc khai thác các nguồn tài nguyên này sẽ dễ dàng hơn rất nhiều. Lựa chọn kinh tế hay khí hậu là bài toán đang được đặt ra và gây nhiều tranh cãi.
Ý chính của bài viết trên là gì?
 Xem đáp án
Xem đáp án
Chọn C
Phương pháp giải:
Dựa vào nội dung đoạn trích, phân tích.
Giải chi tiết:
Ý chính của bài viết là: Khủng hoảng khí hậu ở Bắc Cực và những hệ lụy.
Câu 11:
Theo đoạn 2 của bài viết, phần lớn lượng carbon ở Bắc Cực nằm ở đâu?
 Xem đáp án
Xem đáp án
Chọn D
Phương pháp giải:
Căn cứ bài đọc hiểu, tìm ý.
Giải chi tiết:
Phần lớn lượng carbon nằm ở: trong lòng đất – lưu trữ khoảng 50% lượng carbon trong lòng đất trên thế giới.
Câu 12:
Cụm từ “dữ liệu vệ tinh” trong đoạn 3 để chỉ loại dữ liệu về điều gì?
 Xem đáp án
Xem đáp án
Chọn A
Phương pháp giải:
Căn cứ bài đọc hiểu, phân tích.
Giải chi tiết:
“Dữ liệu vệ tinh” để chỉ: Dữ liệu về độ bao phủ băng.
Câu 13:
Theo đoạn 3, có thể kết luận gì về các khí nhà kính?
 Xem đáp án
Xem đáp án
Chọn A
Phương pháp giải:
Căn cứ bài đọc hiểu, phân tích.
Giải chi tiết:
Theo nhận định của chuyên gia về khí metan: "Khí carbon dioxide và metan thoát ra từ các địa điểm tan băng vĩnh cửu và các vụ cháy, chúng không chỉ tồn tại ở Bắc Cực mà sẽ hòa vào khí quyển và lưu thông trên toàn cầu, góp phần làm tăng nồng độ khí nhà kính". Từ đó, có thể kết luận là: Chúng được tạo ra ở một nơi những có thể gây tác động ở nơi khác.
Câu 14:
Ở đoạn 4, tác giả so sánh lớp băng bao phủ vùng cực với “tấm gương khổng lồ” nhằm mục đích gì?
 Xem đáp án
Xem đáp án
Chọn D
Phương pháp giải:
Căn cứ bài đọc hiểu, phân tích.
Giải chi tiết:
Đầu đoạn tác giả khẳng định “vùng cực trái đất có nhiệt độ lạnh” sau đó chỉ là 2 nguyên nhân: 1-ít nhận được ánh nắng mặt trời trực tiếp; 2-các khối băng như “tấm gương khổng lồ” phản xạ hầu hết ánh sáng mặt trời về không gian.
Mục đích là: Minh họa cho một đặc điểm khiến khi hậu các vùng cực vô cùng lạnh giá.
Câu 15:
Khí hậu ấm lên ở vùng cực ảnh hưởng thế nào tới nền khí hậu chung của Trái Đất?
 Xem đáp án
Xem đáp án
Chọn A
Phương pháp giải:
Căn cứ bài đọc hiểu, phân tích.
Giải chi tiết:
Sự ảnh hưởng là: Phá vỡ vòng tuần hoàn nhiệt trên hành tinh. Vì băng Bắc Cực tác động đến dòng hải lưu. Đại dương và không khí hoạt động như động cơ nhiệt, vận chuyển nhiệt đến các cực một cách thường xuyên thông qua hoàn lưu khí quyển và dòng hải lưu đề tạo ra sự cân bằng. Diện tích băng biển giảm sẽ ảnh hưởng đến những quá trình này. Nhiệt độ vùng cực ấm lên phá vỡ lưu lượng nhiệt tổng thể của Trái Đất, trong khi hướng gió thay đổi đẩy nhiều băng hơn từ biển Bắc Cực về phía Đại Tây Dương. Tại đây, chúng sẽ tan thành nước lạnh và ngăn cản dòng hải lưu ấm lưu chuyển từ vùng nhiệt đới.
Câu 16:
Từ “lãnh nguyên” là khái niệm chỉ điều gì?
 Xem đáp án
Xem đáp án
Chọn B
Phương pháp giải:
Căn cứ bài đọc hiểu, tìm ý.
Giải chi tiết:
“Lãnh nguyên” được hiểu là: một dạng sinh thái.
Câu 17:
Bài viết đề cập tới ngôi làng Russkoye Ustye nhằm minh hoạ điều gì?
 Xem đáp án
Xem đáp án
Chọn B
Phương pháp giải:
Căn cứ bài đọc hiểu, tìm ý.
Giải chi tiết:
Biến đổi khí hậu khiến người dân nơi đây bị đau đầu, các bệnh về da,… Họ không thể đi xe trượt tuyết trong tháng 6, các loài cá lặn sâu xuống dưới đáy biển.
Mục đích khi đề cập đến ngôi làng là: Biến đổi khí hậu đang làm đảo lộn cuộc sống của người dân bản địa.
Câu 18:
Tại sao các chính trị gia có vẻ đang làm ngơ trước thực trạng biến đổi khí hậu tại vùng cực?
 Xem đáp án
Xem đáp án
Chọn A
Phương pháp giải:
Căn cứ bài đọc hiểu, tìm ý.
Giải chi tiết:
Các nhà chính trị làm ngơ vì: Họ quan tâm tới những lợi ích kinh tế và địa chính trị tại các nơi này hơn.
Câu 19:
Ở cuối bài viết, tác giả bày tỏ thái độ gì?
 Xem đáp án
Xem đáp án
Chọn B
Phương pháp giải:
Căn cứ bài đọc hiểu, phân tích.
Giải chi tiết:
Thái độ của họ là: Hoài nghi.
Câu 20:
Thí sinh đọc bài và trả lời câu hỏi từ 20 – 27:
Đằng sau phát minh ra penicillin của Fleming
Việc khám phá ra penicillin, một trong những loại kháng sinh đầu tiên trên thế giới, đánh dấu một bước ngoặt trong lịch sử loài người - khi mà cuối cùng con người đã tìm ra được một phương thuốc để chữa khỏi những bệnh nhân mắc các bệnh nhiễm trùng chết người.
Bất kỳ học sinh nào ở phổ thông cũng được học rằng: “Penicillin do tiến sĩ Alexander Fleming - một nhà vi khuẩn học ở bệnh viện St. Mary. London, phát hiện ra vào tháng 9 năm 1928”. Sau chuyến nghỉ hè ở Scotland, Fleming quay trở lại phòng thí nghiệm và tình cờ phát hiện một loại nấm có tên Penicillium notatum đã mọc đầy trên đĩa thí nghiệm của mình. Sau khi cẩn thận đưa chiếc đĩa lên kính hiển vi, ông đã ngỡ ngàng khi thấy loại nấm kia đã ngăn chặn thành công sự phát triển bình thường của vi khuẩn. Fleming phải mất vài tuần sau mới có thể nuôi lại đủ lượng nấm mốc đó để xác thực được phát hiện của mình, ông đi đến kết luận khiến giới khoa học thời đó ngỡ ngàng: “Có một số thành phần bên trong nấm Penicillium notatum không những có thể kìm hãm sự phát triển của vi khuẩn mà quan trọng hơn, chúng còn có thể được khai thác để chống lại các bệnh truyền nhiễm”.
Thực ra, Fleming không có đủ điều kiện thí nghiệm cũng như kiến thức nền tảng về hóa học để thực hiện những bước quan trọng tiếp theo giúp phân lập thành phần hoạt tính của nấm Penicillium, làm sạch chúng và chỉ ra được dòng vi khuẩn mà chúng có thể diệt được. Tất cả những công việc sau này đều do Howard Florey, giám đốc điều hành của Viện Nghiên cứu về Bệnh học của Đại học Oxford, tiến hành. Tiến sĩ Howard Florey là một bậc thầy trong lĩnh vực chiết tách và đồng thời có trong tay hàng loạt những nhà khoa học tài năng. Công trình nghiên cứu này bắt đầu từ năm 1938 khi Florey, người từ lâu đã quan tâm đến cách vi khuẩn và nấm mốc tiêu diệt nhau trong tự nhiên, đã tình cờ đọc được bài báo của Fleming về nấm Penicillium trên Tạp chí Bệnh học Thực nghiệm. Ngay sau đó, Florey và đồng nghiệp cùa ông đã họp trong phòng thí nghiệm tối tàn của mình và quyết định sẽ làm sáng tỏ bản chất khoa học trong phát hiện của Fleming về hoạt tính chống vi khuẩn của nấm Penicillium notatum.
Suốt mùa hè năm 1940. Họ tập trung vào thử nghiệm trên 50 con chuột sau khi chúng bị cho nhiễm một loại vi khuẩn chết người. Một nửa số chuột đã chết vi nhiễm trùng máu trong khi nửa còn lại được tiêm penicillin và đã sống sót. Đỏ cùng là lúc mà Florey bước tiếp đến việc thử nghiệm trên người. Nhưng vấn đề là làm sao cỏ đủ penicillin nguyên chất đề điều trị cho người. Mặc cho những nỗ lực tăng hiệu suất chiết tách lên nhiều lần nhưng vẫn cần tới 2.000 lít dịch nuôi cấy nấm để có thể tách ra đủ penicillin cho một ca nhiễm trùng máu ở người.
Tháng 9 năm 1940, một nhân viên bào vệ tên là Albert Alexander ở Oxford đã được thử nghiệm thuốc lần đầu tiên. Alexander bị tai nạn khi làm việc trong vườn hoa hồng của trường và bị nhiễm trùng rất nghiêm trọng. Florey nghe được câu chuyện một cách tình cờ và đã ngay lập tức đề nghị bệnh xá của trường cho ông thử dùng penicillin để điều trị ca bệnh này. Chỉ 5 ngày sau khi tiêm, Alexander có dấu hiệu hồi phục. Nhưng tiếc thay. Florey không có đủ penicillin để điều trị dứt điểm, nên cuối cùng Alexander vẫn không thể qua khỏi.
Mùa hè năm 1941, ngay trước khi Mỹ tham gia Chiến tranh Thể giới thử II, Florey cùng 40 đồng nghiệp đã bay đến Mỹ và hợp tác với các nhà khoa học ờ đây nhằm tìm ra một phương pháp khác để sản xuất penicillin với năng suất cao hơn. Vào một ngày hè oi ả, một thư ký phòng thí nghiệm là cô Mary Hunt xuất hiện với một quà bí bị mốc vàng phủ kín. Thật tình cờ, giống nấm mốc đó là Penicillinum chrysogeum, có chứa lượng penicillin cao gấp 200 lần loài nấm mà Fleming tìm ra. Dù phải xử lý vô cùng phức tạp nhưng cuối cùng mẻ chiết tách đầu tiên vẫn thu được lượng penicillin cao gấp 1.000 lần so với lần đầu tiên do chính Florey thực hiện ờ Anh.
Trên thực tế, Fleming đà nghiên cứu rất ít về penicilin sau khi phát hiện ra nó năm 1928. Tuy nhiên, sau đó, từ năm 1941, khi các phóng viên viết bài về những thử nghiệm kháng sinh trên người đã không tìm hiểu kĩ nên chi ghi nhận tiến sĩ Fleming là người duy nhất khám phá ra penicillin. Cũng vì sự im lặng của Florey mà công sức của ông và đồng nghiệp – các nhà khoa học ở Oxford - đã gần như bị bỏ qua. Vấn đề sau này đã phần nào được khắc phục khi cà Fleming và Florey cùng các cộng sự của ông được nhận giài Nobel “Sinh lý hay Y học” năm 1945.
Ý chính của bài viết trên là gì?
 Xem đáp án
Xem đáp án
Chọn A
Phương pháp giải:
Dựa vào nội dung đoạn trích, phân tích.
Giải chi tiết:
Ý chính của bài là: Florey góp công trong việc đưa penicillin vào sử dụng.
Câu 21:
Từ nào dưới đây gần nghĩa nhất với từ “kìm hãm”?
 Xem đáp án
Xem đáp án
Chọn D
Phương pháp giải:
Dựa vào nội dung bài từ đồng nghĩa, phân tích tìm từ phù hợp.
Giải chi tiết:
Từ gần nghĩa với “kìm hãm” là: ngăn cản.
Câu 22:
Đâu KHÔNG phải là điều kiện giúp tiến sĩ Howard Florey phát triển nghiên cứu về penicillin?
 Xem đáp án
Xem đáp án
Chọn B
Phương pháp giải:
Dựa vào nội dung đoạn trích, phân tích.
Giải chi tiết:
Yếu tố không phải là điều kiện giúp tiến sĩ Howard Florey phát triển nghiên cứu về penicillin là: Có đủ penicillin để thử nghiệm trên người.
Câu 23:
Có thể suy luận điều gì từ việc điều trị cho nhân viên bảo vệ Alexander?
 Xem đáp án
Xem đáp án
Chọm B
Phương pháp giải:
Dựa vào nội dung đoạn trích, phân tích.
Giải chi tiết:
Việc điều trị cho nhân viên bảo vệ có thể suy ra: penicillin có tiềm năng trị bệnh nhiễm trùng trên người. Sau khi được điều trị bằng penicillin người bảo vệ đã có rất nhiều tiến triển tốt, tuy nhiên do lượng penicillin không đủ nên mới dẫn đến cái chết của người bảo vệ.
Câu 24:
Bố cục của đoạ 5 đặc trưng cho thể loại nào sau đây?
 Xem đáp án
Xem đáp án
Chọn C
Phương pháp giải:
Dựa vào các thể loại đã học.
Giải chi tiết:
Đoạn 5 đặc trưng cho thể tự sự (kể chuyện). Đoạn này kể lại câu chuyện về ông bảo vệ - người đầu tiên được chữa trị bằng penicillin, tuy nhiên lượng penicillin không đủ nên đã qua đời.
Câu 25:
Nấm Penicillin chrysogeum có đặc điểm gì nổi trội?
 Xem đáp án
Xem đáp án
Chọn C
Phương pháp giải:
Dựa vào nội dung đoạn trích, phân tích.
Giải chi tiết:
Đặc điểm nổi trội của nấm penicillin chrysogeum là: Có hàm lượng penicillin cao hơn hàm lượng penicillin chiết xuất từ nấm penicillin notatum.
Câu 26:
Tại sao nói công sức của các nhà khoa học ở Oxford gần như bị bỏ qua?
 Xem đáp án
Xem đáp án
Chọn B
Phương pháp giải:
Dựa vào nội dung đoạn trích, phân tích.
Giải chi tiết:
Có thể nói công sức của nhà khoa học Florey gần như bị bỏ qua vì các nhà báo không nhắc đến họ trong khi Florey cũng không lên tiếng.
Câu 27:
Đoạn cuối thể hiện ngụ ý gì của tác giả?
 Xem đáp án
Xem đáp án
Chọn B
Phương pháp giải:
Dựa vào nội dung đoạn trích, phân tích.
Giải chi tiết:
Đoạn văn cuối đã thể hiện: Công sức của Florey và các đồng nghiệp cuối cùng cũng đã được ghi nhận vì họ đã nhận được giải thưởng Nobel.
Câu 28:
Thí sinh đọc bài đọc và trả lời câu hỏi từ 28 đến 35:
Ô nhiễm và nhiễm độc chì
Từ thời Ai Cập cổ đại người ta đã dùng chì oxide (PbO) dưới dạng một chất rắn màu vàng để làm men gốm. Khi nung ở nhiệt độ cao, PbO nóng chảy và hợp nhất với các nguyên liệu khác trong thành phần của men tạo thành một màng thủy tinh mỏng và bỏng trên bề mặt gốm, nhờ đó gốm không thấm nước và không dễ bám bẩn. PbO sẽ trở thành mối nguy hiểm nếu sử dụng không đúng cách: khi tiếp xúc với chất lỏng có tính axit, một phần PbO trong men bị hòa tan. Trong một vài giờ hoặc một vài ngày, nồng độ ion chì II (Pb2+) trong chất lỏng đó sẽ lên tới hàng trăm hoặc thậm chí hàng ngàn phần triệu. Vì vậy, nếu bình gốm tráng men chì được dùng để chứa thực phẩm lỏng có tính axit thì thực phẩm sẽ bị nhiễm chì.
Thực tế cho thấy, bát đĩa tráng men chứa chì vẫn đang là nguồn chính gây nhiễm độc chì qua đường ăn uống, đặc biệt là ở các nước đang phát triển. Nghiên cứu cho thấy sau khi vào cơ thể người, chì được máu phân phối đi khắp cơ thể và tích lũy trong xương. Tùy thuộc vào mức độ phơi nhiễm, chì có thể ảnh hưởng xấu đến hệ thần kinh, chức năng thận, hệ miễn dịch, hệ tim mạch và hệ sinh sản và phát triển. Ngày nay ở hầu hết các quốc gia, người ta dùng các nguyên liệu khác thay thế cho PbO trong men gốm vì chúng gần như không bị hòa tan khi sử dụng và do đó an toàn hơn.
Trong suốt lịch sừ nhân loại, nhiều hợp chất cùa chì đã được dùng làm chất màu vì chúng cho màu sắc ổn định và rực rỡ. Chì cromate (PbCrO4) là chất màu vảng tươi có trong loại sơn để sơn vạch và biển chì dẫn giao thông màu vàng. Chì đỏ (Pb3O4) là hỗn hợp oxide của Pb (II) và Pb (IV), có màu đỏ tươi và được trộn vào các loại sơn chống gỉ. Cho đến giữa thế kỷ XX, chì trắng (Pb3CO3)2(OH)2) vẫn được dùng làm thành phần chính trong sơn nội thất màu trắng. Các chất màu chứa chì từng được dùng để in tạp chí và giấy gói thực phẩm. Thậm chí, ở nhiều thế kỷ trước, các muối chì còn được dùng để tạo màu cho thực phẩm.
Ngoài làm men gốm và chất màu, các hợp chất của chì còn được ứng dụng trong nhiều lĩnh vực khác. Chì II arsenate (Pb3(AsO4)2) từng được dùng trong thuốc trừ sâu. Đây là một trong những nguồn gây ô nhiễm Pb2+ cho đất trồng. Chì tetraethyl ((C2H5)4Pb) được pha vào xăng để tăng khả năng chịu nén và tiết kiệm đến 30% lượng xăng cần dùng. PbO sinh ra khi cháy xăng sẽ bám vào các ống xả và thành xi lanh, nên người ta còn trộn vào xăng một chất chứa bromate để PbO chuyển thành muối PbBĩ2 dễ bay hơi và thoát ra ngoài. Vì vậy, đây là một trong những nguồn gây ô nhiễm chì cho không khí và đất ờ những nơi giao thông đông đúc. Một hợp chất khác của chì được dùng trong nhựa PVC để cải thiện độ bền nhiệt và độ bền tia cực tím cho loại nhựa này. Điều này đang gây áp lực vể môi trường cho các nhà máy tái chế nhựa thải.
Trong xây dựng, vì bền màu hơn sơn không chì nên sơn chứa chì thường được quét lên những bề mặt chịu nhiều va chạm như tủ bếp và viền cửa sổ Tuy nhiên, khi lớp sơn bong ra, trẻ nhỏ có thể nhặt lên ăn vì Pb2+ có vị ngọt. Một nghiên cứu ờ Mỹ cho thay, trẻ nhỏ ở các khu ổ chuột nội thành, nơi những lớp sơn cũ vẫn đang tiếp tục bong tróc, thường có nồng độ chì trong máu cao. Vì vậy, những người cải tạo nhà cũ được khuyến nghị thu gom đúng cách bụi từ các lớp sơn cũ. Từ năm 1978, ờ Mỹ đã quy định nồng độ chì trong sơn không được vượt quá 600 ppm. Còn ở Trung Quốc, Ấn Độ và một số nước châu Á khác, cho đến nay chất màu chứa chì vẫn đang được 40 dùng rộng rãi trong sơn nội thất, đôi khi ờ mức vượt quá 180.000 ppm.
Ớ các vùng đô thị, bụi ngọt đang là nguồn nguy cơ lớn đối với sức khóc cùa trẻ nhò. Chúng được tích lũy từ vô số vật liệu và hoạt động của con người như bụi sơn, gốm sứ, nhựa, xăng, các nhà máy tái chế và cả thuốc nhuộm tóc. Mặc dù nồng độ chì trong môi trường vẫn đang gia tăng ờ một số nơi trên thế giới, nhưng tình trạng sử dụng tràn lan các hợp chất chứa chì dẫn đến không kiểm soát được mức độ phát thải đã giảm đáng kể trong vài thập kỷ qua ở nhiều nước phát triển. Nhờ vậy, nồng độ chì trong đất, nước và không khí ở những vùng đó đã giảm tương đối nhiều.
Ý chính của bài viết trên là gì?
 Xem đáp án
Xem đáp án
Chọn C
Phương pháp giải:
Căn cứ nội dung bài đọc hiểu.
Giải chi tiết:
Nội dung chính của đoạn trích nói đến các hợp chất của chì có nhiều tính chất quý nhưng độc nên đã được hạn chế sử dụng.
Câu 29:
Cụm từ “mức độ phơi nhiễm” có nghĩa là gì?
 Xem đáp án
Xem đáp án
Chọn D
Phương pháp giải:
Căn cứ nội dung bài đọc hiểu.
Giải chi tiết:
“Mức độ phơi nhiễm” là một thuật ngữ thuộc lĩnh vực y học, được sử dụng để chỉ sự tiếp xúc giữa vùng da tổn thương hay niêm mạc của người không bị bệnh với máu, mô hoặc dịch cơ thể của người mắc bệnh.
-> Trong bài đọc, mức độ phơi nhiễm ở đây được hiểu là thời gian chì tiếp xúc với không khí.
Câu 30:
Theo đoạn 1 và 2, phát biểu nào dưới đây KHÔNG đúng?
 Xem đáp án
Xem đáp án
Chọn C
Phương pháp giải:
Căn cứ nội dung bài đọc hiểu.
Giải chi tiết:
Ngày nay ở hầu hết các quốc gia, người ta dùng các nguyên liệu khác thay thế cho PbO trong men gốm vì chúng gần như không bị hòa tan khi sử dụng và do đó an toàn hơn.
Như vậy, câu “Chì oxide là thành phần không thể thay thế trong men gốm” là phát biểu không chính xác.
Câu 31:
Từ đoạn 3, ta có thể suy luận gì về màu sắc của các hợp chất của chì?
 Xem đáp án
Xem đáp án
Chọn A
Phương pháp giải:
Căn cứ nội dung bài đọc hiểu.
Giải chi tiết:
Trong suốt lịch sừ nhân loại, nhiều hợp chất cùa chì đã được dùng làm chất màu vì chúng cho màu sắc ổn định và rực rỡ.
=> Màu sắc các hợp chất chì rất bền và tươi sáng.
Câu 32:
Nhận định nào dưới đây thể hiện rõ nhất nội dung của đoạn 4?
 Xem đáp án
Xem đáp án
Chọn B
Phương pháp giải:
Căn cứ nội dung bài đọc hiểu.
Giải chi tiết:
Đoạn 4 đề cập tới ứng dụng của chì trong nhiều lĩnh vực khác. Tuy nhiên, những hợp chất này có gây ô nhiễm môi trường. Điển hình như:
- Chì II arsenate (Pb3(AsO4)2) là một trong những nguồn gây ô nhiễm Pb2+ cho đất trồng.
- Chì tetraethyl ((C2H5)4Pb) là một trong những nguồn gây ô nhiễm chì cho không khí và đất ờ những nơi giao thông đông đúc.
- Một hợp chất khác của chì được dùng trong nhựa PVC để cải thiện độ bền nhiệt và độ bền tia cực tím cho loại nhựa này. Điều này đang gây áp lực vể môi trường cho các nhà máy tái chế nhựa thải.
=> Như vậy, nhận định đúng nhất nội dung của đoạn 4 là “Nhiều hợp chất của chì đang gây ô nhiễm môi trường”.
Câu 33:
Vì sao trẻ nhỏ sống trong các khu ổ chuột ở Mỹ ăn lớp sơn bong chứa chì?
 Xem đáp án
Xem đáp án
Chọn C
Phương pháp giải:
Dựa vào nội dung đoạn trích.
Giải chi tiết:
Sơn chứa chì được sử dụng trên bề mặt va chạm nhiều như tủ bếp hoặc viền cửa sổ. Khi lớp sơn bong ra, trẻ nhỏ có thể nhặt lên ăn vì Pb2+ có vị ngọt.
=> Trẻ nhỏ ở các khu ổ chuột Mĩ thường ăn lớp sơn bóng chứa chì vì sơn có vị ngọt.
Câu 34:
Ở đoạn 5, tác giả muốn ngụ ý điều gì khi so sánh nồng độ chì trong sơn ở Mỹ với các nước châu Á?
 Xem đáp án
Xem đáp án
Chọn B
Phương pháp giải:
Căn cứ bài đọc hiểu.
Giải chi tiết:
Một nghiên cứu ờ Mỹ cho thay, trẻ nhỏ ở các khu ổ chuột nội thành, nơi những lớp sơn cũ vẫn đang tiếp tục bong tróc, thường có nồng độ chì trong máu cao. Vì vậy, những người cải tạo nhà cũ được khuyến nghị thu gom đúng cách bụi từ các lớp sơn cũ. Từ năm 1978, ở Mỹ đã quy định nồng độ chì trong sơn không được vượt quá 600 ppm.
=> Như vậy, việc so sánh nồng độ chì trong sơn ở Mĩ với các nước Châu Á cho thấy từ nghiên cứu chỉ ra nồng độ chì trong máu của người dân ở các khu ổ chuột cao, Mĩ đã hành động sớm để hạn chế các hợp chất của chì trong sơn.
Câu 35:
Có thể kết luận gì về tình trạng sử dụng tràn lan các hợp chất chì ở các nước phát triển?
 Xem đáp án
Xem đáp án
Chọn C
Phương pháp giải:
Căn cứ bài đọc hiểu.
Giải chi tiết:
Mặc dù nồng độ chì trong môi trường vẫn đang gia tăng ờ một số nơi trên thế giới, nhưng tình trạng sử dụng tràn lan các hợp chất chứa chì dẫn đến không kiểm soát được mức độ phát thải đã giảm đáng kể trong vài thập kỷ qua ở nhiều nước phát triển.
=> Tình trạng sử dụng tràn lan các hợp chất chì ở các nước phát triển đã giảm đáng kể.
Câu 36:
Từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8, 9 lập được bao nhiêu số tự nhiên gồm 3 chữ số đôi một khác nhau và số đó chia hết cho 3.
 Xem đáp án
Xem đáp án
Chọn A
Phương pháp giải:
Bước 1: Gọi số cần tìm là
Tách các bộ số chia hết cho 3, chia 3 dư 1 và chia 3 dư 2.
Bước 2: Xét các trường hợp bộ số chia hết cho 3
+) a, b, c đều chia hết cho 3
+)
+) .
+) Trong 3 số a, b, c có 1 số chia hết cho 3, 1 số chia 3 dư 1, 1 số chia 3 dư 2.
Giải chi tiết:
Bước 1:
Gọi số cần tìm là
Từ các số bài cho ta chia thành 3 bộ số:
+ Bộ số chia hết cho 3 là: 3; 6; 9
+ Bộ số chia cho 3 dư 1 là: 1; 4; 7
+ Bộ số chia cho 3 dư 2 là: 2; 5; 8
Bước 2:
Xét các trường hợp sau:
+) a, b, c đều chia hết cho 3 Có 3! số.
+) => Có 3! số.
+) ⇒ Có 3!số.
+) Trong 3 số a, b, c có 1 số chia hết cho 3, 1 số chia 3 dư 1, 1 số chia 3 dư 2
Vậy có 3.3!+162=180 số thỏa mãn đề bài.
Câu 37:
Cho S là tập nghiệm của bất phương trình . Số giá trị nguyên của tham số m để (1;2) Ì S là
 Xem đáp án
Xem đáp án
Chọn B
Phương pháp giải:
Bước 1: Tìm điều kiện xác định
Bước 2: Sử dụng phương pháp đưa về cùng cơ số và tìm điều kiện của m.
Bước 3: Dựa vào điều kiện nguyên của m và (1;2)⊂S tìm m.
Giải chi tiết:
Bước 1: Điều kiện
Bước 2: Ta có:
Bước 3 : Vì nên bài toán trở thành tìm m nguyên để hệ bất phương trình nghiệm đúng với mọi
Tương đương với hai bất phương trình: nghiệm đúng với mọi và bất phương trình nghiệm đúng với mọi
Ta xét nghiệm đúng với mọi
Tương tự với nghiệm đúng với mọi
Ta có
Vậy
Vì m nguyên nên m là các số nguyên thỏa mãn −6≤m≤22, tức là có 22−(−6)+1=29 giá trị của m thỏa mãn bài toán.
Câu 38:
Trong không gian với hệ trục tọa độ vuông góc Oxyz, cho 4 điểm A(1;5;4), B(-3;1;4),
C(5;4;1), D(-2;1;-3). Bán kính mặt cầu ngoại tiếp tứ diện ABCD bằng
 Xem đáp án
Xem đáp án
Phương pháp giải:
Bước 1: Viết phương trình mặt phẳng trung trực của AB, BC, CD.
Bước 2: Khi đó giao điểm I của 3 mặt phẳng là tâm mặt cầu ngoại tiếp tứ diện ABCD, tìm bán kính IA.
Giải chi tiết:
Bước 1: Viết phương trình mặt phẳng trung trực của AB, BC, CD.
Ta có:
Trung điểm của AB là:
Trung điểm của BC là:
Trung điểm của AB là:
Phương trình mặt phẳng trung trực của
Phương trình mặt phẳng trung trực của
Phương trình mặt phẳng trung trực của CD:
Bước 2: Khi đó giao điểm I của 3 mặt phẳng là tâm mặt cầu ngoại tiếp tứ diện $A B C D$, tìm bán kính IA.
Gọi I là giao điểm của 3 mặt phẳng trung trực vừa tìm được
Khi đó ta có tọa độ của I thỏa mãn hệ
Vậy bán kính đường tròn ngoại tiếp tứ diện ABCD bằng 5.
Câu 39:
Gọi V1,V2, lần lượt là thể tích của khối tứ diện đều và khối lập phương có chung mặt cầu
ngoại tiếp. Khi đó, bằng
 Xem đáp án
Xem đáp án
Phương pháp giải:
Bước 1: Lập tỉ lệ giữa cạnh của hình tứ diện đều và bán kính mặt cầu ngoại tiếp, tỉ lệ giữa cạnh hình lập phương và bán kính mặt cầu ngoại tiếp
Bước 2: Lập tỉ số về thể tích giữa tứ diện đều và mặt cầu ngoại tiếp, giữa hình lập phương và mặt cầu ngoại tiếp.
Bước 3: Tính
Giải chi tiết:
Bước 1: Gọi a là độ dài cạnh của tứ diện đều khi đó ta có:
Gọi b là độ dài hình lập phương, ta có:
Bước 2: Tỉ số cạnh của tứ diện đều và lập phương có cùng mặt cầu ngoại tiếp
Bước 3: Tính
Thể tích tứ diện đều cạnh a là
Thể tích khối lập phương cạnh b là :
Vậy tỉ lệ thể tích:
Chọn D.
Câu 40:
Xét các số phức z thỏa mãn . Giá trị nhỏ nhất của biểu thức bằng
 Xem đáp án
Xem đáp án
Phương pháp giải:
Bước 1: Tìm tập hợp biểu diễn số phức thỏa mãn |z−i|=|z+3i| và biểu diễn trên mặt phẳng tọa độ.
Bước 2: Biểu diễn số phức trên mặt phẳng tọa độ và tìm giá trị nhỏ nhất của
là độ dài đoạn thẳng nối hai điểm biểu diễn của z và z0
Giải chi tiết:
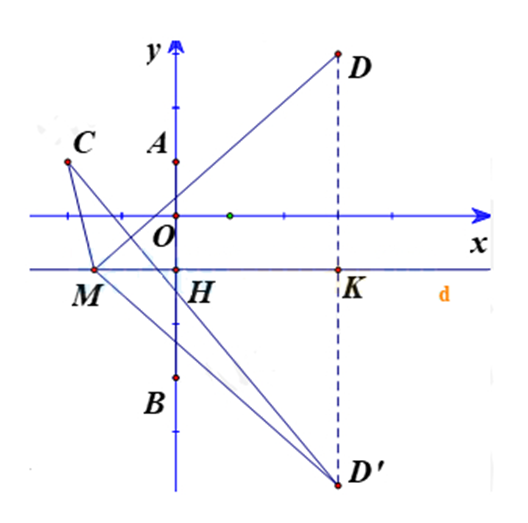
Bước 1: Tìm tập hợp biểu diễn số phức thỏa mãn và biểu diễn trên mặt phẳng tọa độ.
Gọi A(0;1) là điểm biểu diễn số phức i
B(0;−3) là điểm biểu diễn số phức −3i
M(a;b) là điểm biểu diễn số phức
Khi đó tương đương với điểm M là điểm thỏa mãn: MA=MB
Khi đó tập hợp điểm M là đường trung trực d của đoạn thẳng AB.
Gọi H là trung điểm của AB
Ta có đường thẳng .
Bước 2: Biểu diễn số phức trên mặt phẳng tọa độ và tìm giá trị nhỏ nhất của
Gọi C, D lần lượt là điểm biểu diễn số phức
Khi đó bài toán trở thành tìm giá trị nhỏ nhất của MC+MD.
Lấy điểm D’ đối xứng D qua d.
Đường thẳng DD’ qua D và vuông góc với đường thẳng d có phương trình là: x=3
⇒ Giao điểm của DD’ và d là K(3;-1)
K là trung điểm của DD’ nên D’(3;-5)
Vậy giá trị nhỏ nhất của là
Chọn A
Câu 41:
Một lô hàng có 30 sản phẩm trong đó có 5 phế phẩm. Lấy ngẫu nhiên đồng thời 6 sản phẩm của lô hàng đó. Xác suất để trong 6 sản phẩm lấy ra có không quá 2 phế phẩm là
 Xem đáp án
Xem đáp án
Phương pháp giải:
Bước 1: Tính không gian mẫu
Bước 2: Gọi A là biến cố “Lấy được k quá hai phế phẩm”Tính
Bước 3: Tính xác suất
Giải chi tiết:
Bước 1: Tính không gian mẫu
Trong 30 sản phẩm có 5 phế phẩm và 25 thành phẩm
Không gian mẫu là số cách chọn 6 sản phẩm trong 30 sản phẩm:
Bước 2: Gọi A là biến cố “Lấy được k quá hai phế phẩm”Tính
Gọi A là biến cố “Trong 6 sản phẩm lấy được không quá 2 phế phẩm.
Ta cần tính khả năng của A
TH1: Không có phế phẩm ⇒Có cách chọn
TH2: Có 1 phế phẩm ⇒Có cách chọn
TH3: Có 2 phế phẩm ⇒Có cách chọn
Vậy
Bước 3: Tính xác suất
Xác suất để lấy được không quá 2 phế phẩm là:
Chọn A
Câu 42:
Cho một tấm tôn hình vuông có cạnh bằng a. Người ta cắt 4 góc của tấm tôn để được một tấm tôn mới như hình vẽ.
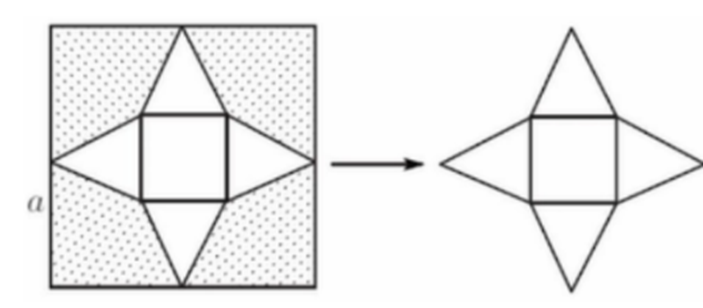
Từ tấm tôn mới, người ta gặp được một hình chóp tứ giác đều. Để khối chóp thu được có thể tích lớn nhất thì diện tích các miếng tốn bỏ đi là
 Xem đáp án
Xem đáp án
Phương pháp giải:
Gọi x là độ dài của cạnh đáy của khối chóp
hh là chiều cao của khối chóp, h′ là chiều cao của tam giác cân ở mặt bên của khối chóp.
Bước 1: Biểu diễn h và thể tích V của khối chóp theo a và x
Bước 2: Tìm max của với x>0
Bước 3: Tìm phần diện tích bị bỏ
Giải chi tiết:
Gọi x là độ dài của cạnh đáy của khối chóp
h là chiều cao của khối chóp, h′ là chiều cao của tam giác cân ở mặt bên của khối chóp.
Bước 1: Biểu diễn h và thể tích V của khối chóp theo a và x
Ta có:
Ta có:
Thể tích khối chóp:
Bước 2: Tìm max của với x > 0.
Xét hàm số với x > 0
Ta có:
Dấu "=" xảy ra khi và chỉ khi
Bước 3: Tìm phần diện tích bị bỏ
Vậy diện tích bị bỏ là .
Chọn B
Câu 43:
Một nhà máy sản xuất bóng đèn trang trí với chi phí sản xuất 12 USD mỗi bóng đèn. Nếu giá bán mỗi bóng đèn là 20 USD thì nhà máy dự tính bán được 2000 bóng mỗi tháng. Nếu cứ tăng giá bán mỗi bóng đèn lên 1 USD thì số bóng đèn bán được mỗi tháng giảm đi 100 bóng đèn. Để nhà máy có lợi nhuận lớn nhất, giá bán mỗi bóng đèn là
 Xem đáp án
Xem đáp án
Phương pháp giải:
Bước 1: Gọi x là số tiền tăng thêm của một tháng và biểu diễn số tiền bán 1 tháng theo x.
Bước 2: Biểu diễn lợi nhuận theo x. Áp dụng BĐT Cauchy để tìm max.
Giải chi tiết:
Bước 1: Gọi x là số tiền tăng thêm của một tháng và biểu diễn số tiền bán 1 tháng theo x.
Số tiền bán mỗi bóng đèn là: 20+x(USD)
Số tiền lãi của 1 bóng đèn là: x+8 (USD)
Sau khi tăng xx USD 1 bóng đèn thì số bóng bán được trong 1 tháng: 2000−100x
Bước 2: Biểu diễn lợi nhuận theo x. Áp dụng BĐT Cauchy để tìm max.
Dấu “=” xảy ra ⇔800+100x=2000−100x⇔x=6
Vậy số tiền mỗi bóng là 20+6=26 USD.
Chọn C
Câu 44:
Số nghiệm nguyên của bất phương trình là
 Xem đáp án
Xem đáp án
Phương pháp giải:
Bước 1: Đặt .
Bước 2: Giải bất phương trình
Giải chi tiết:
Bước 1: Đặt
TXĐ:
Đặt
Bước 2: Giải bất phương trình
BPT trở thành:
Vậy có 2 nghiệm nguyên của bất phương trình.
Chọn ACâu 45:
Một người vay ngân hàng với số tiền 50.000.000 đồng, mỗi tháng trả góp số tiền 4.000.000 đồng vào cuối tháng và phải trả lãi suất cho số tiền chưa trả là 1% một tháng theo hình thức lãi kép. Theo quy định, nếu người vay trả trước hạn thì sẽ chịu thêm phí phạt bằng 3% số tiền trả trước hạn. Hết tháng thứ 6, người đó muốn trả hết nợ. Tổng số tiền người đó phải trả cho ngân hàng là
 Xem đáp án
Xem đáp án
Phương pháp giải:
Bài toán trên trả góp như sau: Sau tháng thứ nhất thì người đó nợ 50.(1+1%) triệu đồng.
Trả hết 4 triệu thì hết tháng 1 còn nợ 50.(1+1%)−4triệu
Tháng thứ hai thì nợ thêm 1% số tiền nợ của tháng 1 nên số nợ lúc này là [50.(1+1%)−4](1+1%)
Cứ như thế đến tháng thứ 6.
Tính số tiền đã trả góp trong 6 tháng.
Đến hết tháng 6 thì cần trả số tiền còn nợ + tiền phạt
Số tiền nợ sau N tháng:
T: tiền vay; r: lãi suất 1 tháng; A: Tiền trả hàng tháng
Giải chi tiết:
Số tiền trả góp tháng là: 4.6=24 triệu
Áp dụng CT tính số tiền còn nợ sau N tháng ta có:
Số tiền còn nợ sau 6 tháng:
Người này muốn trả hết số tiền trên thì phải trả thêm 3% số tiền đó
Số tiền cần trả lúc này là: ≈29,322 (triệu đồng)
Vậy tổng số tiền người đó đã trả là: 24+29,322=53,322(triệu)
Câu 46:
Cho hình chóp S ABC có SA ^ ( ABC ), tam giác ABC vuông tại B , SA = BC = a , AC = 2 a. Khoảng cách từ điểm A đến mặt phẳng (SBC) là
 Xem đáp án
Xem đáp án
Phương pháp giải:
Bước 1: Kẻ AH vuông góc với SB. Chứng minh AH⊥(SBC)
Bước 2: Tính AH
Giải chi tiết:
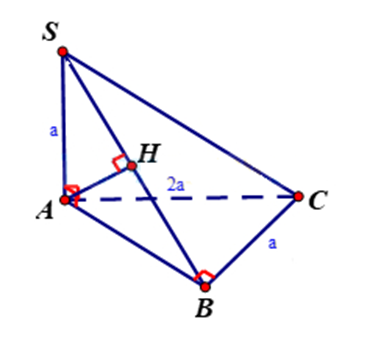
Bước 1: Kẻ AH vuông góc với SB. Chứng minh
Kẻ AH vuông góc với SB.
Ta có:
Lại có
Bước 2: Tính AH
Xét tam giác vuông ABC có:
Xét tam giác vuông SAB có:
Chọn D
Câu 47:
Hình sau là đồ thị của hàm số (với ).
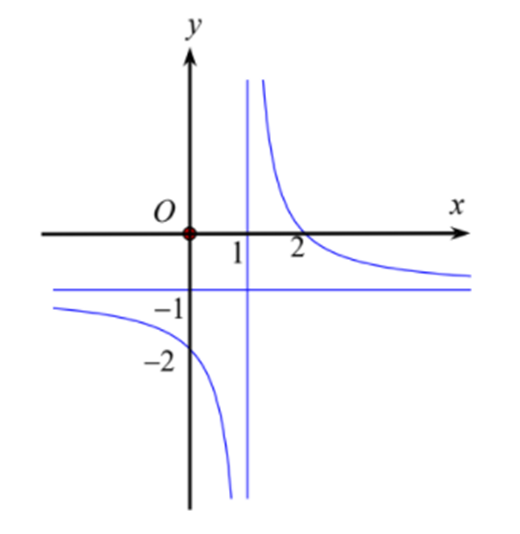
Khi đó ab - c bằng
 Xem đáp án
Xem đáp án
Phương pháp giải:
Bước 1: Tính giới hạn của hàm số tại vô cực để tính a, tìm đường tiệm cận đứng, từ đó tìm c
Bước 2: Thay tọa độ điểm (0;−2) vào hàm số tìm b, tính ab−c.
Giải chi tiết:
Bước 1: Tính giới hạn của hàm số tại vô cực để tính a, tìm đường tiệm cận đứng, từ đó tìm c
Ta có:
Bước 2: Thay tọa độ điểm (0;−2) vào hàm số tìm b, tính ab−c.
Thay tọa độ của (0;−2) vào ta được:.
Chọn D
Câu 48:
Cho hình phẳng D được giới hạn bởi các đường và như hình vẽ (phần màu vàng)
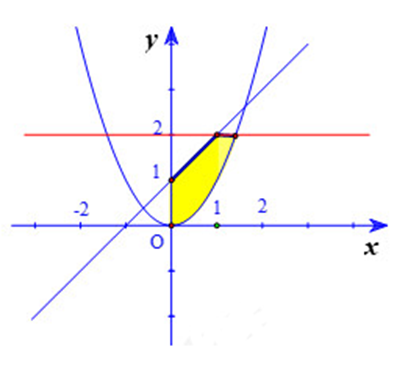
Diện tích của D là:
 Xem đáp án
Xem đáp án
Phương pháp giải:
Bước 1: Tách hình tô đậm thành hiệu của hai hình: . Trong đó là phần tạo bởi các đường là phần tạo bởi các đường .
Bước 2: Tính
Bước 3: Tính
Giải chi tiết:
Bước 1: Tách hình tô đậm thành hiệu của hai hình:
Phần tô đậm của hình bằng .
Trong đó là phần tạo bởi các đường .
là phần tạo bởi các đường .
Bước 2: Tính
Hoành độ giao điểm bởi các đường là:
Vì x > 0 nên:
Bước 3: Tính . Ta có: .
Chọn A
Câu 49:
Tính tổng tất cả các nghiệm của phương trình .
 Xem đáp án
Xem đáp án
Phương pháp giải:
Bước 1: Sử dụng công thức
Bước 2: Giải phương trình và tính tổng nghiệm
Giải chi tiết:
Bước 1: Sử dụng công thức . Ta có:
Bước 2: Giải phương trình và tính tổng nghiệm
Vậy tổng nghiệm bằng 0.
Chọn D
Câu 50:
Trong không gian với hệ trục tọa độ vuông góc Oxyz, cho mặt phẳng , mặt cầu . Gọi là đường thẳng nằm trong mặt phẳng P, đi qua và cắt (S) tại 2 điểm M, N. Độ dài đoạn thẳng MN nhỏ nhất là
 Xem đáp án
Xem đáp án
Phương pháp giải:
Tìm tâm I, bán kính R của mặt cầu (S) và vtpt của mặt phẳng (P)
Giải chi tiết:
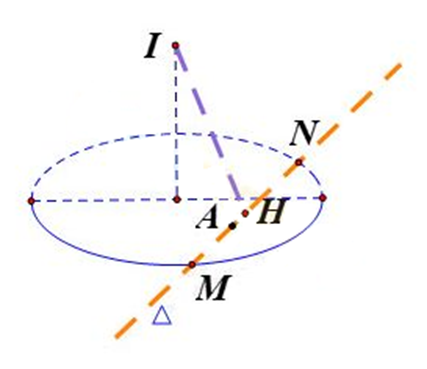
Mặt cầu (S) có tâm I(5;2;3), bán kính .
Mặt phẳng (P) có .
Ta có: => Mặt phẳng (P) cắt mặt cầu (S).
⇒ Điểm A nằm trong mặt cầu.
Gọi H là trung điểm của MN. Khi đó IH vuông góc với MN
Do đó MN min ⇔ IH max
Vì tam giác IAH vuông tại H
=> MN min .
Chọn B
Câu 51:
Cho hình nón có bán kính đáy bẳng a. Thiết diện qua trục của hình nón là một tam giác đều. Thể tich khối nón đã cho bằng
 Xem đáp án
Xem đáp án
Phương pháp giải:
Bước 1: Xác định chiều cao của hình nón.
Bước 2: Tính thể tích hình nón
Giải chi tiết:
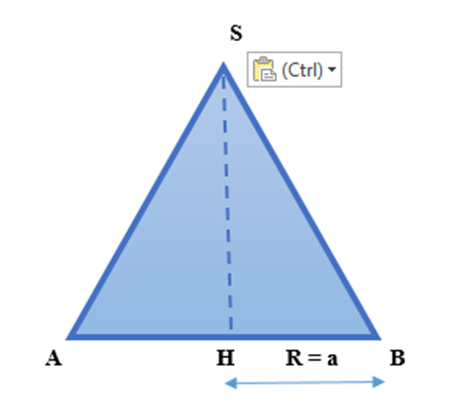
Bước 1: Xác định chiều cao của hình nón.
Ta có: .
Bước 2: Tính thể tích hình nón
Thể tích hình nón là: .
Chọn C
Câu 52:
Một ô tô đang chạy thì người lái đạp phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc trong đó t (giây) là khoảng thời gian tính từ lúc bắt đầu đạp phanh và a là một hằng số dương. Biết rằng từ lúc đạp phanh đến khi dừng hẳn, ô tô di chuyển được 36m. Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Phương pháp giải:
Bước 1: Tìm thời gian dừng hẳn theo a.
Bước 2: Áp dụng công thức giữa vận tốc và quãng đường từ đến : .
Giải chi tiết:
Bước 1: Tìm thời gian dừng hẳn theo a.
Thời điểm đạp phanh thì t=0
Thời điểm xe dừng hẳn thì có vận tốc v=0
Khi đó
Bước 2: Áp dụng công thức giữa vận tốc và quãng đường, tìm a.
Quãng đường từ thời điểm t=0 đến thởi điểm là:
Vậy .
Chọn D
Câu 53:
Cho hàm số y = f(x) Biết hàm số y = f ' (x)là hàm số bậc 4 trùng phương có đồ thị như hình vẽ.
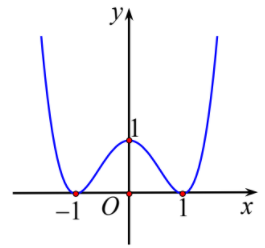
Số điểm cực trị của hàm số là
 Xem đáp án
Xem đáp án
Phương pháp giải:
Bước 1: Tính đạo hàm y’
Bước 2: Dựa vào đồ thị để tìm số cực trị
Giải chi tiết:
Bước 1: Tính đạo hàm y’
Bước 2: Dựa vào đồ thị để tìm số cực trị
Đặt
Dựa vào đồ thị ta có: có đúng 1 nghiệm.
Vậy hàm số có 1 cực trị.
Chọn D
Câu 54:
Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình vẽ. Số các giá trị nguyên của m để phương trình có đúng ba nghiệm phân biệt thuộc đoạn là
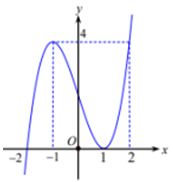
 Xem đáp án
Xem đáp án
Phương pháp giải:
Bước 1: Sử dụng phương pháp ghép trục
Bước 2: Biện luận m
Giải chi tiết:
Bước 1: Sử dụng phương pháp ghép trục
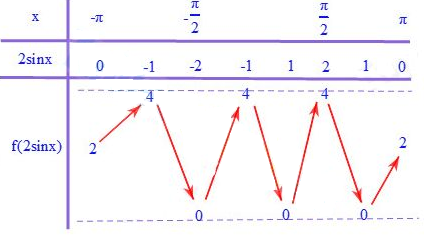
Bước 2: Biện luận m
Từ bảng trên ta thấy để phương trình có đúng ba nghiệm phân biệt thuộc đoạn thì .
Khi đó .
Vậy 4 giá trị của m thỏa mãn.
Chọn C
Câu 55:
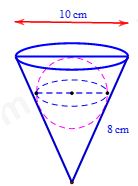
Bạn An có một cốc hình nón có đường kính đáy là 10cm và độ dài đường sinh là 8cm. Bạn dự định đựng một viên bị hình cầu sao cho toàn bộ viên bi nằm trong cốc (không phân nào của viên bị cao hơn miệng cốc). Hỏi bạn An có thể đựng được viên bị có đường kính lớn nhất bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Phương pháp giải:
Bước 1: Xét thiết diện qua trục.
Bước 2: Xác định vị trí của viên bi thỏa mãn bài toán
Bước 3: Tính đường kính viên bi
Áp dụng công thức tính bán kính đường tròn nội tiếp với
Giải chi tiết:
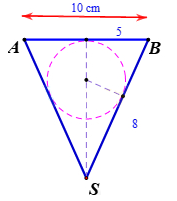
Bước 1: Xét thiết diện qua trục.
Thiết diện qua trục là một tam giác cân có cạnh bên là 8cm và cạnh đáy là 10 cm (tam giác SAB)
Bước 2: Xác định vị trí của viên bi thỏa mãn bài toán
Viên bi bị cắt theo chính thiết diện đó thì sẽ tiếp xúc với hai cạnh bên.
Viên bi càng tiến gần đáy thì càng lớn.
Để viên bị có đường kính lớn nhất thì viên bi phải tiếp xúc với mặt trên của cốc nước (miễn là viên bi không cao hơn miệng cốc)
Bước 3: Tính đường kính viên bi
Câu 56:
"Vừa gà vừa chó.
Bó lại cho tròn.
Ba mượi sáu con.
Một trăm chân chã̃n".
Hỏi số gà nhiều hơn số chó mấy con?
 Xem đáp án
Xem đáp án
Phương pháp giải:
Bước 1: Đặt ẩn, số gà là x và số chó là y
Bước 2: Biểu diễn bài toán theo ẩn x và y và tìm nghiệm.
Giải chi tiết:
Bước 1: Đặt ẩn, số gà là x và số chó là y
Gọi số con gà là x con (x>0) và số con chó là y con
Bước 2: Biểu diễn bài toán theo ẩn x và y và tìm nghiệm.
Theo bài ta có x+y=36 và 2x+4y=100.
Ta có hệ phương trình .
Số gà nhiều hơn số chó là 22−14=8.
Chọn A
Câu 57:
Trong không gian với hệ trục tọa độ vuông góc Oxyz, cho đường thẳng và mặt phẳng . Phương trình đường thẳng d’ đối xứng với d qua (P) là
 Xem đáp án
Xem đáp án
Phương pháp giải:
Bước 1: Lấy điểm B(0;−1;2) thuộc d.
Bước 2: Tìm giao điểm A của d và (P)
Bước 3: Gọi H là hình chiếu của B lên (P), B’ là điểm đối xứng B qua (P). Tìm d’
Giải chi tiết:
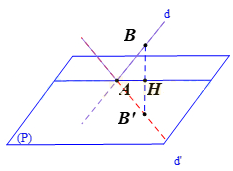
Bước 1: Lấy điểm B(0;−1;2) thuộc d.
Bước 2: Tìm giao điểm A của d và (P)
Gọi A là giao điểm của d và (P).
Khi đó . Thay vào (P) ta được:
=> A(1;1;1)
Bước 3: Tìm d’
Gọi H là hình chiếu của B lên (P), B’ là điểm đối xứng B qua (P).
Khi đó H là trung điểm của BB’
Đường thẳng BH đi qua B(0;-1;2) và nhận làm vecto chỉ phương có phương trình là:
. Thay vào (P) ta được:
Vecto chỉ phương của AB’ là:
Đường thẳng
Chọn B
Câu 58:
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Biết với H thuộc cạnh AB thỏa mãn AB=3AH. Góc tạo bởi SA và mặt phẳng (ABC) bằng . Khoảng cách giữa hai đường thẳng SA và BC là
 Xem đáp án
Xem đáp án
Phương pháp giải:
Bước 1: Chứng minh HF⊥(SAK)
Bước 2: Chứng tỏ và tìm khoảng cách .
Giải chi tiết:
Kẻ Ax song song với BC
Kẻ HK vuông góc với Ax, kẻ HF vuông góc với SK.
Bước 1: Chứng minh HF⊥(SAK)
Ta có
Bước 2: Chứng tỏ và tìm khoảng cách.
Ta có
Tam giác ABC đều nên
Góc tạo bởi SA và ( ABC ) bằng nên
Áp dụng HTL trong tam giác vuông SHK ta có:
Vậy .
Chọn C
Câu 59:
Tập hợp tất cả các giá trị m để hàm số đồng biến trên R là
 Xem đáp án
Xem đáp án
Phương pháp giải:
Bước 1: Tính y'.
Bước 2: Tìm m
Hàm số đồng biến trên
Giải chi tiết:
Bước 1: Tính y'.
Bước 2: Tìm m
Hàm số đồng biến trên
Vì
Dấu "=" xảy ra khi
Chọn A
Câu 60:
Các nghiệm của phương trình được biểu điển hình học bởi điểm A và điểm B trên mặt phẳng tọa độ. Độ dài của AB là
 Xem đáp án
Xem đáp án
Phương pháp giải:
Bước 1: Tìm A và B
Bước 2: Tính độ dài AB.
Giải chi tiết:
Bước 1: Tìm A và B
Ta có:
Chọn
Bước 2: Tính độ dài AB.
Độ dài đoạn thẳng AB là:
Chọn C
Câu 61:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và góc BAD = 60°. Hình chiếu vuông góc của S lên mặt phẳng đáy là trọng tâm G của tam giác BCD, góc giữa SA và đáy bằng 60°
a) Tính thể tích khối chóp S.ABCD.
b) Tính khoảng cách giữa hai đường thẳng AC và SB.
 Xem đáp án
Xem đáp án
a) Phương pháp giải:
Bước 1: Tính AG.
Bước 2: Xác định góc giữa SA và đáy trên hình.
Bước 3: Tính SG
Bước 4: Tính thể tích S.ABCD.
Giải chi tiết:
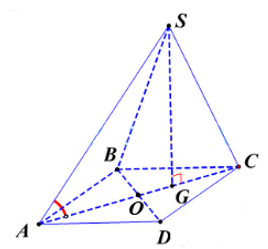
Bước 1: Tính AG.
Gọi O là giao điểm của AC và BD.
ABCD là hình thoi cạnh a nên .
=> Tam giác $B C D$ là tam giác đều
Bước 2: Xác định góc giữa SA và đáy trên hình.
Do SG vuông góc với (ABCD) nên góc giữa SA và đáy bằng góc giữa SA và hình chiếu của nó trên (ABCD) tức là góc giữa SA và .
Bước 3: Tính SG
Tam giác vuông SAG có nên
Bước 4: Tính thể tích S.ABCD.
Ta có
Diện tích hình thoi ABCD là:
Thể tích S.ABCD: .
b) Phương pháp giải:
Kẻ Bx song song với AC. Kẻ GH vuông góc với Bx, GK vuông góc với SH
Bước 1: Chứng minh GK⊥(SBH)
Bước 2: Chứng minh d(AC,SB)=GK
Bước 3: Tính GK
Giải chi tiết:
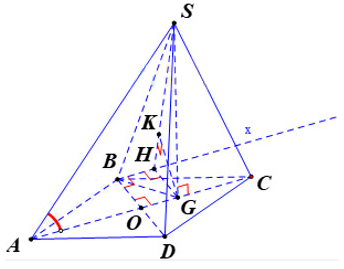
Kẻ Bx song song với AC. Kẻ GH vuông góc với Bx, GK vuông góc với SH
Bước 1: Chứng minh
Ta có:
Bước 2: Chứng minh
Ta có
Mà
Bước 3: Tính GK
Dễ thấy tứ giác OBHG là hình chữ nhật .
Áp dụng hệ thức lượng trong tam giác vuông SGH ta có:
Vậy
Câu 62:
Trong hình vẽ, xe A kéo xe B bằng một sợi dây dài 39m qua một ròng rọc ở độ cao 12m. Xe A xuất phát từ N và chạy với vận tốc không đổi 2 m/s theo chiều mũi tên.
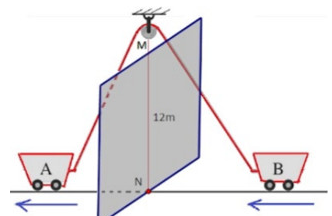
a) Đặt và , (đơn vị mét). Tìm một hệ thức liên hệ giữa x và y .
b) Tính vận tốc của xe B khi xe A cách N một đoạn 5m.
 Xem đáp án
Xem đáp án
a) Phương pháp giải:
Coi M, A, B là một tam giác và N thuộc cạnh AB
Bước 1: Xác định AM+BMAM+BM, MN
Bước 2: Tìm mối liên hệ giữa x và y.
Giải chi tiết:
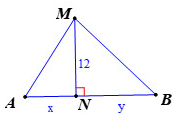
Bước 1: Xác định AM + BM, MN
Coi M,A,B là một tam giác và N thuộc cạnh AB
Sợi dây dài .
Có MN=12.
Bước 2: Tìm mối liên hệ giữa ![]() và y.
và y.
Theo định lý py-ta-go ta được:
Vậy hệ thức cần tìm là
b) Phương pháp giải:
Gọi t là thời gian xe A di chuyển.
Bước 1: Tìm mối quan hệ giữa x và t
Bước 2: Tìm mối quan hệ giữa y và t
Bước 3: Tính quãng đường tại t=2,5(s).
Giải chi tiết:
Bước 1: Tìm mối quan hệ giữa x và t
Khi A sang trái thì x tăng dần và y giảm dần
Tạo mối quan hệ giữa y và t
Vì xe A chuyển động đều với vận tốc là 2m/s nên mối quan hệ giữa x và t là:
Bước 2: Tìm mối quan hệ giữa y và t
Mà ta có nên:
Quãng đường A đi được là 5m nên ta có t=2,5(s)
Bước 3: Tính quãng đường tại t=2,5(s)
Vận tốc tại thời điểm t=2,5(s) của B là y′(2,5). Khi đó
Vậy .
Vận tốc tức thời của xe B tại thời điểm xe A cách N 5m là -0,867(m/s).
