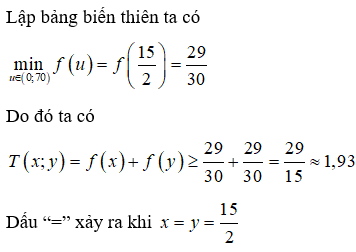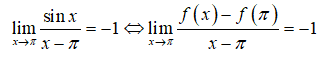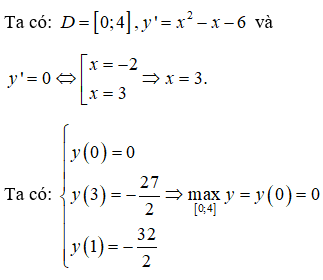25 câu hỏi trắc nghiệm thuộc Đề thi thử THPTQG môn Toán cực hay mới nhất có lời giải - đề 16

Câu 1:

Mặt phẳng (AB'C') chia khối lăng trụ ABC.A'B'C' thành các khối đa diện nào?

A. Một khối chóp tam giác và một khối chóp ngũ giác.

B. Một khối chóp tam giác và một khối chóp tứ giác

C. Hai khối chóp tam giác

D. Hai khối chóp tứ giác

Xem đáp án

Đáp án B

Câu 2:

Cho $f (x) = \sin x$ và $\underset{x \to π}{l i m} \frac{\sin x}{x - π} = - 1 .$ Khẳng định nào dưới đây là đúng?

A. $f' (1) = π$

B. $f' (π) = 1$

C. $f' (π) = - 1$

D. $f' (- 1) = π$

Xem đáp án

Đáp án C

Câu 3:

Cho cấp số nhân $(u_{n})$ , biết $u_{2} = 4$ và tổng hai số hạng đầu bằng 3. Tìm công bội q của cấp số nhân trên.

A. q = 4

B. $q = - \frac{1}{4}$

C. q = -4

D. $q = \frac{1}{4}$

Xem đáp án

Đáp án C

Theo giả thiết, ta có

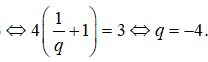
Câu 4:

Trọng tâm các mặt của một hình tứ diện đều tạo thành một hình đa diện mới có tên là gì

A. Tứ diện đều

B. lập phương

C. nhị thập diện đều

D. bát diện đều

Xem đáp án

Đáp án A

Câu 5:

Cho khối lăng trụ đứng có chiều cao là h, đáy là tam giác vuông. Nếu tăng mỗi cạnh góc vuông lên k lần thì thể tích của khối lăng trụ tăng lên bao nhiêu lần?

A. $3 k^{2}$

B. $4 k^{2}$

C. $2 k^{2}$

D. $k^{2}$

Xem đáp án

Đáp án D

Gỉa sử khố lăng trụ đứng có đáy là ABC vuông tại A.

Ta có

Câu 6:

Số điểm cực trị của hàm số $y = x + \sqrt{2 x^{2} + 1}$ là:

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Đáp án B

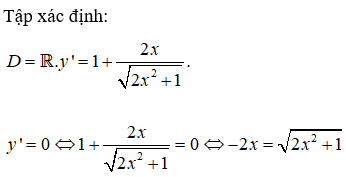
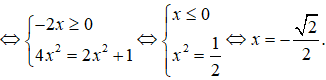
Bảng biến thiên:

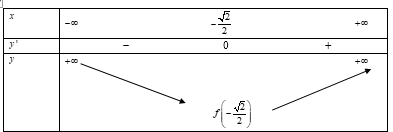
Vậy hàm số có 1 điểm cực trị.

Câu 7:

Cho bài toán: “Xét tính đơn điệu của hàm số $y = \sqrt{x^{2} + 2 x - 3}$ ” Một bạn học sinh đã làm bài như sau:

Bước 1: Tập xác định: $D = ℝ \ (- 3; 1)$

Bước 2: Tìm đạo hàm: $y' = \frac{(x^{2} + 2 x - 3)'}{2 \sqrt{x^{2} + 2 x - 3}} = \frac{x + 1}{\sqrt{x^{2} + 2 x - 3}}$

Bước 3: $y' = 0 \Leftrightarrow \{\begin{cases} x + 1 = 0 \\ x^{2} + 2 x - 3 > 0 \end{cases} \Leftrightarrow \{\begin{cases} x = 1 \\ x < - 3 \Leftrightarrow x \in \emptyset; x > 1 \end{cases}$

Bước 4: Bảng biến thiên:

Bước 5: Kết luận:

Vậy hàm số nghịch biến trên nửa khoảng $(- \infty; - 3]$ , đồng biến trên nửa khoảng $[1; + \infty)$ . Hỏi bài làm trên đúng hay

sai? Nếu sai thì sai từ bước nào?

A. Bài làm đúng.

B. Sai từ bước 3.

C. Sai từ bước 4.

D. Sai từ bước 5

Xem đáp án

Đáp án A

Câu 8:

Cho số thực $a \neq 0$ và hàm số $f (x) = \{\begin{cases} \frac{\sqrt[3]{2 x - 1} - 1}{x^{3} - 1}, x \neq 1 \\ x^{2} - 2 x + \frac{6111}{5000} + a^{2}, x = 1 \end{cases}$

Xét 2 phát biểu sau:

(i). Hàm số chắc chắn liên tục từng khoảng $(- \infty; 1] v à (1; + \infty)$ .

(ii). Tồn tại số thực a để hàm số liên tục trên R.

Khẳng định nào dưới đây là đúng?

A. (i), (ii) đều đúng

B. (i) sai, (ii) đúng

C. (i) đúng, (ii) sai

D. (i), (ii) đều sai

Xem đáp án

Đáp án A

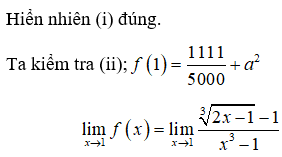
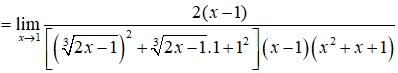
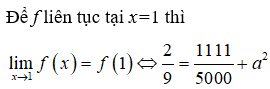
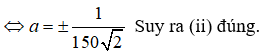
Câu 9:

Cho hàm số y = f(x) liên tục trên R, có đồ thị của đạo hàm f'(x) như sau:

Hỏi mệnh đề nào sau đây là đúng?

A. Hàm số đồng biến trên khoảng $(1; + \infty)$ .

B. Hàm số nghịch biến trên khoảng $(- \infty; - 1)$ .

C. Hàm số đồng biển trên khoảng $(- \infty; - 3)$

D. Hàm số đồng biến trên khoảng (-1;1)

Xem đáp án

Đáp án C

Đồ thị trên là của đạo hàm f'(x)

f(x) sẽ đồng biến trên khoảng mà

Câu 10:

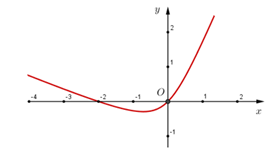
Cho hàm số y = f(x) liên tục trên R , có đồ thị của đạo hàm f'(x) như sau:

Trong các mệnh đề sau, mệnh đề nào sai?

A. f đạt cực tiểu tại x = 0

B. f đạt cực tiểu tại x =-2

C. f đạt cực đại tại x = -2

D. Cực tiểu của f nhỏ hơn cực đại

Xem đáp án

Đáp án B

Nhìn đồ thị, ta thấy f' đổi dấu từ dương sang âm khi đi qua điểm x = -2, do đó x = -2 là điểm cực đại của hàm f => C đúng, B sai.

Tương tự, f’ đổi dấu từ âm sang dương khi đi qua điểm x = 0, do đó x = 0 là điểm cực tiểu của hàm f => A đúng.

Câu 11:

Tìm giá trị lớn nhất của hàm số $y = \frac{x^{3}}{3} - \frac{x^{2}}{2} - 6 x$ trên $[0; 4]$ .

A. $\underset{[0; 4]}{m a x} y = 0$

B. $\underset{[0; 4]}{m a x} y = \frac{22}{3}$

C. $\underset{[0; 4]}{m a x} y = - \frac{27}{2}$

D. $\underset{[0; 4]}{m a x} y = \frac{32}{3}$

Xem đáp án

Đáp án A

Câu 12:

Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a, gọi $φ$ là góc giữa hai mặt phẳng $(S A B) v à (C S D)$ . Tính $\cos φ$

A. $\cos φ = \frac{1}{2}$

B. $\cos φ = \frac{1}{6}$

C. $\cos φ = \frac{1}{3}$

D. $\cos φ = \frac{1}{4}$

Xem đáp án

Đáp án C

Câu 13:

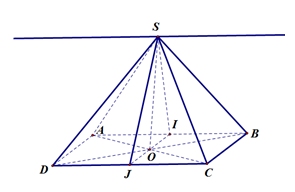
Cho tứ diện OABC có OA, OB, OC, OD đôi một vuông góc nhau, biết rằng $O A = 2 O B = 3 O C = 3 a$ . Tính khoảng cách d từ O đến mặt phẳng (ABC).

A. $d = \frac{2 a}{\sqrt{14}}$

B. $d = \frac{3 a}{\sqrt{13}}$

C. $d = \frac{3 a}{\sqrt{11}}$

D. $d = \frac{3 a}{\sqrt{10}}$

Xem đáp án

Đáp án A

Gọi I là hình chiếu của O trên BC, H là hình chiếu của O trên AI.

Suy ra d = OH.

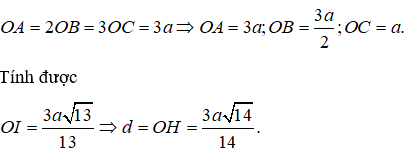
Câu 14:

Gọi a là giá trị thực để hàm số $f (x) = \{\begin{cases} \frac{\sqrt{\cos x} - \sqrt[3]{\cos x}}{\sin^{2} x} k h i x \neq 0 \\ a + 1 k h i x \neq 0 \end{cases}$ liên tục tại x = 0. Gía trị $P = \sqrt{2 a^{4} + 11}$ gần với số nào nhất dưới đây?

A. 3,32

B. 3,31

C. 3,61

D. 3,92

Xem đáp án

Đáp án C

$= \frac{1}{2}$

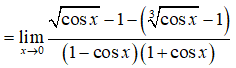
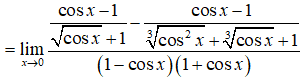
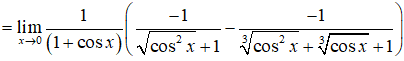
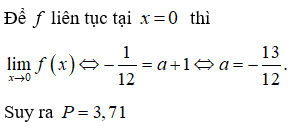
Câu 15:

Gọi $(∆)$ là tiếp tuyến của đường cong $(C) : y = \frac{x^{2} - x + 1}{x + 1}$ . Biết rằng $(∆)$ qua điểm (-1;0). Tính khoảng cách d từ điểm M(1;-1) đến $(∆)$

A. $d = \frac{2}{5}$

B. $d = \frac{1}{5}$

C. d = 1

D. d = 2

Xem đáp án

Đáp án D

Câu 16:

Cho hình lập phương ABCD.A'B'C'D' có cạnh là a. Tính thể tích khối tứ diện ABC'D' theo a?

A. $\frac{a^{2}}{6}$

B. $\frac{a^{3}}{2}$

C. $\frac{a^{3}}{4}$

D. $\frac{a^{3}}{3}$

Xem đáp án

Đáp án D

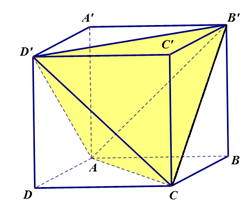
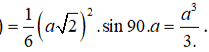
Câu 17:

Biết rằng mức lương của một kỹ sư ở công ty X trong quý I năm 2017 (3 tháng đầu tiên của năm 2017) là $S_{0}$ (triệu đồng), kể từ quý II mức lương sẽ được tăng thêm 0,5 triệu đồng mỗi quý. Tổng lương của kỹ sư đó tính từ quý I năm 2017 đến hết quý IV năm 2022 là 1002 (triệu đồng). Tính tổng lương S (triệu đồng) của kỹ sư tính từ quý I năm 2017 đến hết quý IV năm 2015.

A. S = 1611

B. S = 342

C. S = 324

D. S = 1911

Xem đáp án

Đáp án A

Từ quý I năm 2017 đến hết quý IV năm 2022 là 24 quý.

Tổng lương chính là tổng của cấp ố cộng với

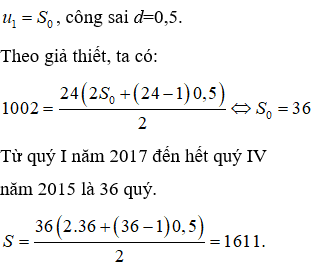
Câu 18:

Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB = a, $A C = a \sqrt{3}$ , tam giác SAB đều và nằm trong mặt phẳng vuông góc đáy. Gọi a (độ) là bởi cạnh SB và mặt phẳng (SAB). Gía trị a gần với số nào nhất dưới đây?

A. 30

B. 40

C. 50

D. 60

Xem đáp án

Đáp án C

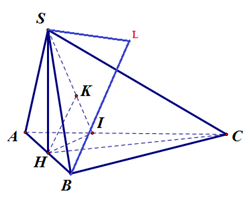
Suy ra K là hình chiếu từ H trên (SAC)

Do đó, nếu gọi L là hình chiếu từ B lên (SAC) thì BL=2HK

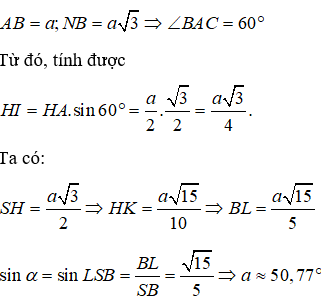
Câu 19:

Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau; AB = 3a, AC = 4a, AD = 5a. Gọi M, N, P lần lượt là trọng tâm của tam giác DAB, DBC, DCA. Tính thể tích của khối chóp DMNA theo a.

A. $V = \frac{10 a^{3}}{27}$

B. $V = \frac{80 a^{3}}{27}$

C. $V = \frac{20 a^{3}}{27}$

D. $V = \frac{40 a^{3}}{27}$

Xem đáp án

Đáp án C

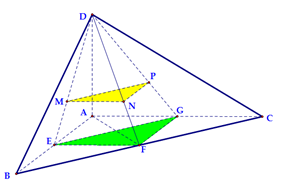
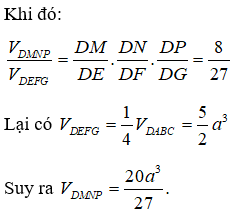
Gọi E,F,G lần lượt là trung điểm của các cạnh AB, BC, AC

Câu 20:

Cho hình chóp tứ giác đều S.ABCD có AB = a, gọi $α$ là góc giữa mặt bên và mặt đáy của hình chóp S.ABCD. Tính khoảng cách d giữa SA và CD theo a và $α$

A. d = a.cos $α$

B. d = a.sin $α$

C. d = a.sin2 $α$

D. d = a.cos2 $α$

Xem đáp án

Đáp án C

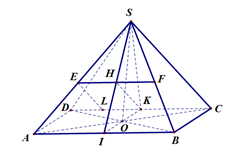
Ta có, CD song song mặt phẳng (SAB) chứa SA nên khoảng cách giữa SA và CD chính là khoảng cách từ CD đến (SAB).

Gọi I, K theo thứ tự là trung điểm AB, CD thì:

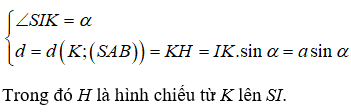
Câu 21:

Cho hàm số $y = \frac{1}{3} x^{3} - m x^{2} + (m^{2} - 4) x + 3$ . Gọi S là tập hợp tất cả các giá trị nguyên của M để hàm số nghịch biến trên khoảng (1;4). Số phần tử của S là:

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Đáp án C

Câu 22:

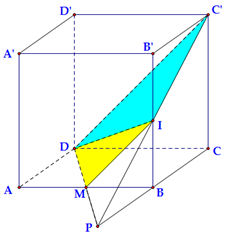
Cho hình lập phương ABCD.A’B’C’D’. I là trung điểm BB’. Mặt phẳng (DIC’) chia khối lập phương thành 2 phần có tỉ số thể tích phần bé chia phần lớn bằng:

A. 1:3

B. 7:17

C. 4:14

D. 1:2

Xem đáp án

Đáp án B

Câu 23:

Xét các hàm số $f (x) = a x^{2} - \frac{b}{a} x + 3$ và $g (x) = x^{2} - 4 x + 6$ trên đoạn [1;5]. Biết trên đoạn [1;5] thì giá trị lớn nhất của f(x) bằng giá trị nhỏ nhất của g(x) và đạt tại cùng một điểm . Tính S là tổng các giá trị a, b thoả mãn yêu cầu bài toán .

A. S = 0

B. S = -1

C. $S = \frac{1}{2}$

D. không tồn tại S

Xem đáp án

Đáp án C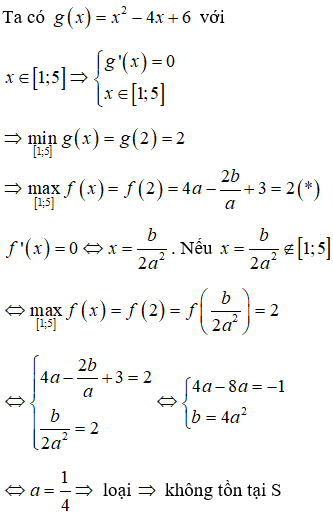

Câu 24:

Cho hàm số $y = x^{3} - 3 m x^{2} + 3 (m^{2} - 1) x - m^{3}$ với m là tham số thực. Gọi S là tập hợp tất cả các giá trị của m sao cho đồ thị hàm số có hai điểm cực trị. Biết rằng khi m thay đổi trong S, các điểm cực đại của đồ thị hàm số cũng thay đổi nhưng luôn nằm trên một đường thẳng (d) cố định . Hỏi (d) song song với đường thẳng nào sau đây:

A. y = 2x + 4

B. y = -3x - 1

C. y = -3x + 5

D. y = -2x

Xem đáp án

Đáp án C

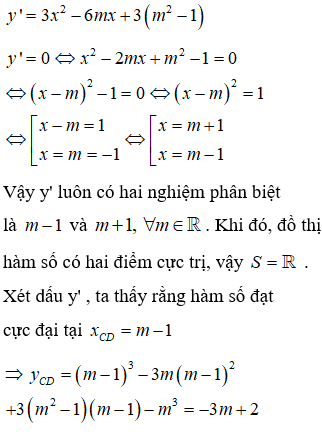
Câu 25:

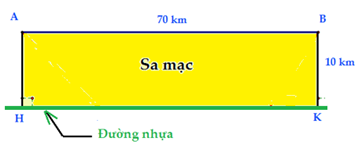
Một nhà địa chất học đang ở tại điểm A trên sa mạc. Anh ta muốn đến điểm B và cách A một đoạn là 70 km. Trong sa mạc thì xe anh ta chỉ có thể di chuyển với vận tốc là 30 km/h. Nhà địa chất ấy phải đến được điểm B sau 2 giờ. Vì vậy, nếu anh ta đi thẳng từ A đến B sẽ không thể đến đúng giờ. May mắn thay, có một con đường nhựa song song với đường nối A và B và cách AB một đoạn 10 km. Trên đường nhựa này thì xe của nhà địa chất học này có thể di chuyển với vận tốc 50 km/h. Tìm thời gian ngắn nhất mà nhà địa chất học có thể đi từ A đến B (đảm bảo trong khung giờ cho phép).

A. 1,83 giờ

B. 1,93 giờ

C. 1,73 giờ

D. 1,86 giờ

Xem đáp án

Đáp án B

Phân tích:

● Ta có thể mô tả bài toán trên bằng hình vẽ sau:

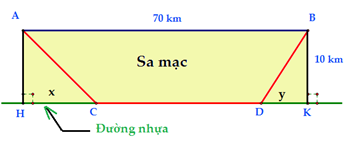
● Như đã phân tích ở trên, nếu đi trực tiếp từ A đến B trên sa mạc với vận tốc và khoảng cách hiện có thì nhà địa chất học không thể đến đúng thời gian quy định

● Vì vậy cần thiết phải chia quãng đường đi được thành 3 giai đoạn:

Giai đoạn 1: đi từ A đến C (từ sa mạc đến đường nhựa song song)

Giai đoạn 2: đi từ C đến D (một quãng đường nào đó trên đường nhựa)

Giai đoạn 3: đi từ D đến B (từ điểm kết thúc D trên đường nhựa đi tiếp đến B băng qua sa mạc).

Goi H, K, C, D là các điểm như hình vẽ.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề thi thử THPTQG môn Toán cực hay mới nhất có lời giải

Đề thi thử THPTQG môn Toán cực hay mới nhất có lời giải - đề 16

Danh sách câu hỏi

Bài thi liên quan